Câu 1: Hãy chọn câu đúng. Tỉ số $\frac{x}{y}$ của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình cùng đơn vị đo là cm.

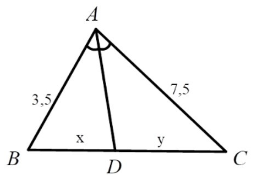
• A. $\frac{7}{15}$

• B. $\frac{1}{7}$
• C. $\frac{15}{7}$
• D. $\frac{1}{15}$

Câu 2: Cho tam giác ABC, đường trung tuyến AM. Tia phân giác của góc AMB cắt AB ở D, tia phân giác của góc AMC cắt AC ở E. Gọi I là giao điểm của AM và DE. Tính độ dài DE, biết BC = 30 cm, AM = 10 cm.

• A. 9 cm
• B. 6 cm
• C. 15 cm

• D. 12 cm

Câu 3: Cho hình vẽ, biết rằng các số trên hình có cùng đơn vị đo. Tính giá trị biểu thức $S = 49x^{2} + 98y^{2}$.

• A. 3400
• B. 4900

• C. 4100

• D. 3600

Câu 4: Cho tam giác ABC, AB = AC = 10 cm, BC = 12 cm. Gọi I là giao điểm của các đường phân giác của tam giác ABC. Tính BI?

• A. 9 cm
• B. 6 cm
• C. 45 cm

• D. $3\sqrt{5}$ cm

Câu 5: Cho $\Delta ABC$, AE là phân giác ngoài của góc A. Hãy chọn câu đúng:

• A. $\frac{AB}{AE}=\frac{BE}{CE}$
• B. $\frac{AE}{AC}=\frac{BE}{CE}$
• C. $\frac{AB}{AC}=\frac{CE}{BE}$

• D. $\frac{AB}{AC}=\frac{BE}{CE}$

Câu 6: Cho tam giác ABC, AB = AC = 10 cm, BC = 12 cm. Gọi I là giao điểm của các đường phân giác của tam giác ABC. Độ dài AI là:

• A. 9 cm
• B. 6 cm

• C. 45 cm

• D. 3 cm

Câu 7: Cho tam giác ABC cân tại A, đường phân giác trong của góc B cắt AC tại D và cho biết AB = 15 cm, BC = 10 cm. Khi đó AD = ?

• A. 3 cm
• B. 6 cm

• C. 9 cm

• D. 12 cm

Câu 8: Cho tam giác ABC vuông tại A có AB = 6, AC = 8. Tia phân giác góc B cắt AC tại D. Độ dài AD là:

• A. 1,5

• B. 3

• C. 4,5
• D. 4

Câu 9: Cho tam giác ABC, $\hat{A}=90^{o}$, AB = 15 cm, AC = 20 cm, đường cao AH $(H \in BC)$. Tia phân giác của $\widehat{HAB}$ cắt HB tại D. Tia phân giác của $\widehat{HAC}$ cắt HC tại E. Tính HE?

• A. 4 cm

• B. 6 cm

• C. 9 cm
• D. 12 cm

Câu 10: Cho $\Delta MNP$, MA là phân giác ngoài của góc M, biết $\frac{NA}{PA}=\frac{3}{4}$. Hãy chọn câu đúng:

• A. $\frac{MN}{MP}=4$
• B. $\frac{MN}{MP}=3$
• C. $\frac{MN}{MP}=\frac{1}{3}$

• D. $\frac{MN}{MP}=\frac{3}{4}$

Câu 11: Cho tam giác ABC có: AB = 4 cm, AC = 5 cm, BC = 6 cm. Các đường phân giác BD và CE cắt nhau ở I. Tỉ số diện tích các tam giác DIE và ABC là:

• A. $\frac{4}{55}$

• B. $\frac{1}{8}$
• C. $\frac{1}{10}$
• D. $\frac{2}{45}$

Câu 12: Cho hình vẽ, biết các số trên hình cùng đơn vị đo. Tỉ số $\frac{x}{y}$ bằng:

• A. $\frac{3}{4}$

• B. $\frac{2}{3}$
• C. $\frac{4}{3}$
• D. Chưa đủ dữ liệu kết luận

Câu 13: Cho ΔMNP, MA là phân giác ngoài của góc M, biết $\frac{NA}{PA}=\frac{1}{3}$. Hãy chọn câu sai:

• A. $\frac{NA}{PA}=\frac{1}{3}$
• B. $\frac{MN}{MP}=\frac{1}{3}$

• C. $\frac{MA}{MP}=\frac{1}{3}$

• D. MP = 3MN

Câu 14: Cho tam giác ABC, AC = 2AB, AD là đường phân giác của tam giác ABC. Khi đó $\frac{BD}{CD}=?$

• A. 1
• B. $\frac{1}{3}$
• C. $\frac{1}{4}$

• D. $\frac{1}{2}$

Câu 15: Hãy chọn câu đúng. Tính độ dài x, y của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình có cùng đơn vị đo là cm.

• A. x = 16 cm; y = 12 cm
• B. x = 14 cm; y = 14 cm
• C. x = 14,3 cm; y = 10,7 cm

• D. x = 12 cm; y = 16 cm

Câu 16: Cho tam giác ABC, AC = 2AB, AD là đường phân giác của tam giác ABC. Xét các khẳng định sau, số khẳng định đúng là:

$(I) \frac{BD}{DC}=\frac{1}{2}$

$(II) \frac{DC}{BC}=\frac{2}{3}$

$(III) \frac{BD}{BC}=\frac{1}{2}$

• A. 0
• B. 3
• C. 1

• D. 2

Câu 17: Cho tam giác ABC có chu vi 18 cm, các đường phân giác BD và CE. Tính các cạnh của tam giác ABC, biết $\frac{AD}{DC}=\frac{1}{2}; \frac{AE}{EB}=\frac{3}{4}$

• A. AC = 4 cm, BC = 8 cm, AB = 6 cm
• B. AB = 4 cm, BC = 6 cm, AC = 8 cm

• C. AB = 4 cm, BC = 8 cm, AC = 6 cm

• D. AB = 8 cm, BC = 4 cm, AC = 6 cm

Câu 18: Cho tam giác ABC vuông tại A có AB = 6, AC = 8. Tia phân giác góc B cắt AC tại D. Độ dài AD là:

• A. 1,5

• B. 3

• C. 4,5
• D. 4

Câu 19: Cho tam giác ABC có: AB = 4 cm, AC = 5 cm, BC = 6 cm. Các đường phân giác BD và CE cắt nhau ở I. Tỉ số diện tích các tam giác DIE và ABC là:

• A. $\frac{4}{55}$

• B. $\frac{1}{8}$
• C. $\frac{1}{10}$
• D. $\frac{2}{45}$

Câu 20: Cho tam giác ABC, đường trung tuyến AM. Tia phân giác của góc AMB cắt AB ở D, tia phân giác của góc AMC cắt AC ở E. Gọi I là giao điểm của AM và DE. Chọn khẳng định đúng.

• A. DE // BC
• B. DI = IE
• C. DI > IE

• D. Cả A, B đều đúng

Câu 21: Cho tam giác ABC, đường trung tuyến AM. Tia phân giác của góc AMB cắt AB ở D, tia phân giác của góc AMC cắt AC ở E. Gọi I là giao điểm của AM và DE. Tính độ dài DE, biết BC = 30 cm, AM = 10 cm.

• A. 9 cm
• B. 6 cm
• C. 15 cm

• D. 12 cm

Câu 22: Cho tam giác ABC có: AB = 12 cm, BC = 15 cm, AC = 18 cm. Gọi I là giao điểm của các đường phân giác và G là trọng tâm tam giác. Chọn khẳng định sai:

• A. IG // BC
• B. $\frac{AI}{ID}=\frac{AG}{GM}$

• C. $\widehat{ABG}=\widehat{CBG}$

• D. $\frac{ID}{AD}=\frac{MG}{MA}$

Câu 23: Cho tam giác ABC có: AB = 12 cm, BC = 15 cm, AC = 18 cm. Gọi I là giao điểm của các đường phân giác và G là trọng tâm tam giác. Độ dài IG là:

• A. 1 cm

• B. 2 cm
• C. 1,5 cm
• D. 2,5 cm

Câu 24: Cho tam giác ABC, AC = 2AB, AD là đường phân giác của tam giác ABC. Xét các khẳng định sau, số khẳng định đúng là:

$(I) \frac{BD}{DC}=\frac{1}{2}$

$(II) \frac{DC}{BC}=\frac{2}{3}$

$(III) \frac{BD}{BC}=\frac{1}{2}$

• A. 0

• B. 3
• C. 1
• D. 2

Câu 25: Cho tam giác ABC, AE là phân giác ngoài của góc A. Hãy chọn câu sai:

• A. $\frac{CE}{AC}=\frac{BE}{AB}$

• B. $\frac{AB}{CE}=\frac{AC}{EB}$

• C. $\frac{AB}{BE}=\frac{AC}{CE}$
• D. $\frac{AB}{AC}=\frac{BE}{CE}$

Câu 26: Tam giác ABC có AB = 6 cm, AC  = 9cm, BC = 10 cm. Đương phân giác trong AD, đường phân giác ngoài AE. Tính độ dài BD, EB

• A. DB = 6 cm; EB = 18 cm
• B. DB = 4 cm; EB = 18 cm

• C. DB = 4 cm; EB = 20 cm

• D. DB = 6 cm; EB = 20 cm

Câu 27: Cho tam giác ABC cân tại A, AB = 10 cm, BC = 12 cm. Gọi I là giao điểm các đường phân giác của tam giác. Tính độ dài AI

• A. 4 cm
• B. 5,5 cm
• C. 6 cm

• D. 5 cm

Câu 28: Cho $\Delta ABC$ vuông ở A, đường phân giác AD. Tính độ dài AB biết DB = 15 cm; DC = 20 cm.

• A. 21 cm

• B. 28 cm
• C. 24 cm
• D. 35 cm

Câu 29: Cho $\Delta ABC$ vuông ở A, đường phân giác BD. Tính độ dài BD, biết AB = 6cm, BC = 10cm.

• A. $2\sqrt{5}$

• B. $3\sqrt{5}$

• C. 7
• D. 8,5

Câu 30: Cho $\Delta ABC$ có AB = 8 cm; AC = 12 cm, đường phân giác AD. Trên đoạn AD lấy điểm E sao cho $\frac{AE}{AC}=\frac{3}{5}$. Gọi K là giao điểm của BE và AC. Tính tỉ số $\frac{AK}{KC}$

• A. $\frac{3}{5}$
• B. $\frac{2}{3}$
• C. $\frac{5}{8}$

• D. $\frac{9}{10}$