NỘI DUNG TRẮC NGHIỆM

Câu 1: Tam giác ABC có BC = a và CA = b. Tam giác ABC có diện tích lớn nhất khi góc C bằng:

• A. 60°

• B. 90°

• C. 150°
• D. 120°

Câu 2: Cho hai tập hợp A = [−1; 3), B = [a; a + 3]. Với giá trị nào của a thì A ∩ B = ∅?

• A. a≥3 hoặc a≤−4
• B.  a>3 hoặc a<−4

• C.  a≥3 hoặc a<−4

• D.  a>3 hoặc a≤−4

Câu 3: Cho hình chữ nhật ABCD có AB = 5cm, BC = 12cm. Độ dài của $\overrightarrow{AC}$ là

• A. 4cm;
• B. 6cm;
• C. 8cm;

• D. 13cm.

Câu 4: Cho mệnh đề P: “∆ABC cân tại A ⇔ AB = AC”. Chọn khẳng định đúng nhất trong các khẳng định sau?

• A. “AB = AC” là điều kiện cần để  “∆ABC cân tại A”;
• B. “AB = AC” là điều kiện đủ để  “∆ABC cân tại A”;
• C. “∆ABC cân tại A” là điều kiện đủ để  “AB = AC”;

• D. “∆ABC cân tại A” là điều kiện cần và đủ để  “AB = AC”.

Câu 5: Cho góc x thỏa mãn 0°<x<90°. Trong các mệnh đề sau, mệnh đề nào sai:

• A. sin x > 0

• B. cos x < 0

• C. tanx > 0
• D. cotx > 0

Câu 6: Đồ thị sau đây là đồ thị của hàm số nào trong các phương án dưới đây?

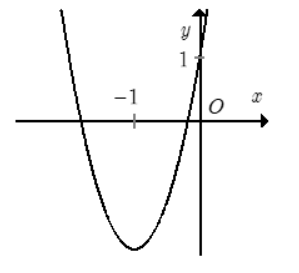
• A. y=−3x$^{2}$−6x

• B. y=3x$^{2}$+6x+1

• C. y=x$^{2}$+2x+1
• D. y=−x$^{2}$−2x+1

Câu 7: Cho tam giác ABC. Tập hợp các điểm M thỏa mãn $\overrightarrow{MA}\times\overrightarrow{BC}=0$ là:

• A. một điểm;

• B. đường thẳng;

• C. đoạn thẳng;
• D. đường tròn.

Câu 8: Cho tam giác ABC có BC = a, CA = b, AB = c. Tính $P=(\overrightarrow{AB}+\overrightarrow{AC})\times\overrightarrow{BC}$

• A. $b^{2}-c^{2}$

• B. $\frac{b^{2}+c^{2}}{2}$
• C. $\frac{c^{2}+b^{2}+a^{2}}{3}$
• D. $\frac{c^{2}+b^{2}-a^{2}}{2}$

Câu 9: Trong các mệnh đề sau mệnh đề nào sai?

• A. Nếu a < b và b < c thì a < c.
• B. Nếu tam giác ABc đều thì nó có 2 góc bằng 60∘

• C. Nếu tứ giác ABCD là hình thoi thì nó là một hình vuông

• D. Nếu a và b chia hết cho c thì a - b cũng chia hết cho c

Câu 10: Cho góc $\widehat{xOy}$=30°. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:

• A. $\frac{3}{2}$
• B. $\sqrt{3}$
• C. $2\sqrt{2}$

• D. 2

Câu 11: Phương trình $\sqrt{x-1}=x-3$ có tập nghiệm là:

• A. {5}

• B. {2}
• C. {2;5}
• D. ∅.

Câu 12: Trong mặt phẳng tọa độ Oxy, cho bốn điểm A(-8;0),B(0;4),C(2;0) và D(-3;-5). Khẳng định nào sau đây là đúng?

• A. Hai góc BAD và BCD phụ nhau
• B. Góc BCD là góc nhọn
• C. $cos(\overrightarrow{AB},\overrightarrow{AD})=cos(\overrightarrow{CB},\overrightarrow{CD})$

• D. Hai góc BAD và BCD bù nhau

Câu 13: Cho tam giác ABC vuông tại A có AB = 3, BC = 5. Tính $|\overrightarrow{AB}+\overrightarrow{BC}|$

• A. 3;

• B. 4;

• C. 5;
• D. 6.

Câu 14: Cho hàm số y=ax$^{2}$+bx+c(a≠0)có đồ thị như hình sau. Khẳng định nào sau đây đúng?

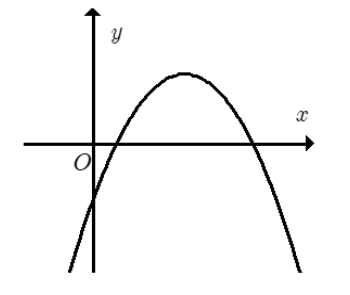
• A. a>0,b<0,c<0;
• B. a>0,b<0,c>0;
• C. a>0,b>0,c>0;

• D. a<0,b>0,c<0.

Câu 15: Tam giác ABC có ba cạnh 6, 8, 10. Khi đó, bán kính đường tròn nội tiếp tam giác ABC là:

• A. $\sqrt{3}$
• B. 4

• C. 2

• D. 1

Câu 16: Xét câu P(n): “n chia hết cho 12”. Với giá trị nào của n sau đây thì P(n) là một mệnh đề đúng?

• A. 48;                                 

• B. 4;
• C. 3;
• D. 88.

Câu 17: Tam thức bậc hai $f(x)=(1-\sqrt{2})x^{2}+(5-4\sqrt{2})x-3\sqrt{2}+6$

• A. Dương với mọi x∈R

• B. Dương với mọi x∈(-3;$\sqrt{2}$)

• C. Dương với mọi x∈(-4;$\sqrt{2}$)
• D. Âm với mọi x∈R

Câu 18: Tập hợp A=(2;+∞)∩[−3;8] bằng tập hợp nào sau đây?

• A. (2;8)

• B. (2;8]

• C. [-3;2)
• D. [-3;+∞)

Câu 19: Cho các tam thức f(x)=2x$^{2}$−3x+4;g(x)=−x$^{2}$+3x−4;h(x)=4−3x$^{2}$. Số tam thức đổi dấu trên R là:

• A. 0 ;

• B. 1 ;

• C. 2. ;
• D. 3.

Câu 20: Miền nghiệm của bất phương trình: 3x + 2(y + 3) > 4(x + 1) - y + 3 là nửa mặt phẳng chứa điểm:

• A. (3;0)
• B. (3;1)

• C. (3;2)

• D. (0;0)

Câu 21: Tìm tập nghiệm của phương trình $\sqrt{4x+1}+5=0$

• A. {2}

• B. ∅.

• C. {−14}
• D. {6}

Câu 22: Tam thức bậc hai f(x)=−x$^{2}$+3x−2 nhận giá trị không âm khi và chỉ khi

• A.x∈(−∞;1)∪(2;+∞)

• B. x∈(1;2)

• C. x∈(−∞;1)∪(2;+∞)
• D. x∈(1;2)

Câu 23: Cho ba điểm A, B, C cùng nằm trên một đường thẳng. Các vectơ $\overrightarrow{AB},\overrightarrow{BC}$ cùng hướng khi và chỉ khi

• A. Điểm B thuộc đoạn AC;

• B. Điểm A thuộc đoạn BC;
• C. Điểm C thuộc đoạn AB;
• D. Điểm B nằm ngoài đoạn AC.

Câu 24: Cho tập hợp A ≠ ∅. Trong các mệnh đề sau, mệnh đề nào SAI?

• A. A ∩ A = A;      

• B. A ∩ ∅ = A;      

• C. A \ A = ∅;       
• D. A ∪ ∅ = A.

Câu 25: Cho 5 điểm M, N, P, Q, R. Tính tổng $\overrightarrow{MN}+\overrightarrow{PQ}+\overrightarrow{RN}+\overrightarrow{NP}+\overrightarrow{QR}$

• A. $\overrightarrow{MR}$

• B. $\overrightarrow{MN}$

• C. $\overrightarrow{PR}$
• D. $\overrightarrow{MP}$

Câu 26: Giá trị nhỏ nhất của biểu thức F(x; y) = y – x trên miền xác định bởi hệ: $\left\{\begin{matrix}y-2x\leq 2\\2y-x\geq 4\\x+y\leq 5\end{matrix}\right.$ là:

• A. min F(x; y) = 1 khi x = 2, y = 3;

• B. min F(x; y) = 2 khi x = 0, y = 2;
• C. min F(x; y) = 3 khi x = 1, y = 4;
• D. min F(x; y) = 7 khi x = 6, y = – 1.

Câu 27: Cho bất phương trình – x + 2 + 2(y – 2) < 2(1 – x). Khẳng định nào dưới đây là khẳng định sai?

• A. Điểm O(0; 0) thuộc miền nghiệm của bất phương trình đã cho;
• B. Điểm B(1; 1) thuộc miền nghiệm của bất phương trình đã cho;

• C. Điểm C(4; 2) thuộc miền nghiệm của bất phương trình đã cho;

• D. Điểm D(1; - 1) thuộc miền nghiệm của bất phương trình đã cho.

Câu 28: Giá trị biểu thức $s=cos^{2}12^{\circ}+cos^{2}48^{\circ}+cos^{2}1^{\circ}+cos^{2}89^{\circ}$ bằng:

• A. 0
• B. 1

• C. 2

• D. 4

Câu 29: Cho hàm số y = f(x) = |-5x|. Khẳng định nào sau đây là sai?

• A. f(-1) = 5
• B. f(2) = 10
• C. f(-2) = 10

• D. f($\frac{1}{5}$)=−1

Câu 30: Cho tam giác ABC và điểm M thỏa mãn $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{0}$ Xác định vị trí điểm M.

• A. M là điểm thứ tư của hình bình hành ACBM;
• B. M là trung điểm của đoạn thẳng AB;
• C. Điểm M trùng với điểm C;

• D. M là trọng tâm của tam giác ABC.

Câu 31: Cho hai tập A = [−2; 1] và B = (0; +∞). Tập hợp A ∪ B là:

• A. [1; +∞);  
• B. [−2;0];    
• C. (0; 1];     

• D. [−2; +∞).

Câu 32: Cặp số nào sau đây là nghiệm của bất phương trình – 2(x – y) + y > 3?

• A. (4; – 4);
• B. (2; 1);
• C. (– 1; – 2);

• D. (4; 4).

Câu 33: Cho số tự nhiên n thỏa mãn $A^{2}_{n}+2C^{n}_{n}=22$ Hệ số của số hạng chứa $x^{3}$ trong khai triển của biểu thức $(3x-4)^{n}$ bằng

• A. – 4320;
• B. – 1440;

• C. 4320;

• D. 1080

Câu 34: Cho tam giác ABC có M là trung điểm của BC, I là trung điểm của AM. Khẳng định nào sau đây đúng ?

• A. $\overrightarrow{AI}=\frac{1}{4}(\overrightarrow{AB}+\overrightarrow{AC})$

• B. $\overrightarrow{AI}=\frac{1}{4}(\overrightarrow{AB}-\overrightarrow{AC})$
• C. $\overrightarrow{AI}=\frac{1}{4}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$
• D. $\overrightarrow{AI}=\frac{1}{4}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AC}$

Câu 35: Cho tam giác ABC. Gọi I là trung điểm AB. Tìm điểm M thỏa mãn hệ thức $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}$

• A. M là trung điểm BC;

• B. M là trung điểm IC;

• C. M là trung điểm IA;
• D. M là điểm trên cạnh IC sao cho IM = 2MC.

Câu 36: Mệnh đề "∃n∈N|n+5>2022" là phủ định của mệnh đề nào sau đây?

• A. ∀n∈N|n+5>2022

• B. ∀n∈N|n+5≤2022

• C. ∃n∈N|n+5=2022
• D. ∃n∈N|n+5≤2022

Câu 37: Xác định tập hợp B={x∈Z|−2≤x<3} bằng cách liệt kê các phần tử.

• A. B = {–2; –1; 1; 2};               
• B. B = {0; 1; 2};   

• C. B = {–2; –1; 0; 1; 2};           

• D. B = {–1; 0; 1; 2}.

Câu 38: Phần không gạch chéo trong hình dưới đây biểu diễn miền nghiệm của bất phương trình nào?

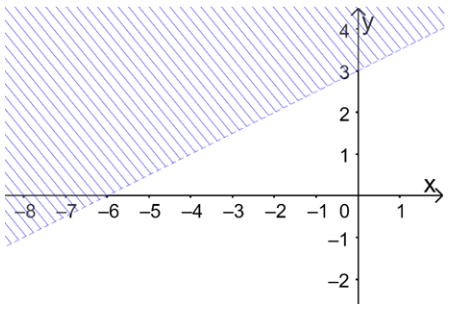
• A. x - 2y + 6 > 0

• B. x−2y+6≥0
• C. x + 2y < 6
• D. x+2y≤6

Câu 39: Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu. Để pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?

• A. 5l nước cam và 4l nước táo
• B. 6l nước cam và 5l nước táo

• C. 4l nước cam và 4l nước táo

• D. 4l nước cam và 6l nước táo

Câu 40: Cho các mệnh đề sau, mệnh đề nào sai:

• A. Một tam giác vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại.  
• B. Một tam giác đều thì có hai trung tuyến bằng nhau và một góc bằng 60∘.       

• C. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một cạnh bằng nhau.

• D. Một tứ giác là hình chữ nhật thì nó có 3 góc vuông.