Câu 1: Tam thức bậc hai $f(x)=x^{2}+(\sqrt{5}-1)x-\sqrt{5}$ nhận giá trị dương khi và chỉ khi 

• A. x∈$(-\sqrt{5};1)$
• B. x∈(−$\sqrt{5}$;+∞);

• C. x∈(−∞;-$\sqrt{5}$)∪(1;+∞);

• D. x∈(−∞;1).

Câu 2: Cho f(x)=ax$^{2}$+bx+c(a≠0). Điều kiện để f(x)>0,∀x∈R là

• A. $\left\{\begin{matrix}a>0\\ \Delta \leq 0\end{matrix}\right.$
• B. $\left\{\begin{matrix}a>0\\ \Delta \geq 0 \end{matrix}\right.$

• C. $\left\{\begin{matrix}a>0\\ \Delta < 0\end{matrix}\right.$

• D. $\left\{\begin{matrix}a<0\\ \Delta > 0\end{matrix}\right.$

Câu 3: Tam thức bậc hai f(x)=−x$^{2}$+3x−2 nhận giá trị không âm khi và chỉ khi

• A.x∈(−∞;1)∪(2;+∞)

• B. x∈(1;2)

• C. x∈(−∞;1)∪(2;+∞)
• D. x∈(1;2)

Câu 4: Tam thức bậc hai $f(x)=(1-\sqrt{2})x^{2}+(5-4\sqrt{2})x-3\sqrt{2}+6$

• A. Dương với mọi x∈R

• B. Dương với mọi x∈(-3;$\sqrt{2}$)

• C. Dương với mọi x∈(-4;$\sqrt{2}$)
• D. Âm với mọi x∈R

Câu 5: Tam thức bậc hai f(x)=−x$^{2}$+5x−6 nhận giá trị dương khi và chỉ khi

• A. x∈(−∞;2)
• B. (3;+∞)
• C. x∈(2;+∞)

• D. x∈(2;+∞)

Câu 6: Các giá trị m để tam thức $f(x)=x^{2}-(m+2)x+8m+1$ đổi dấu 2 lần là:

• A. $m\leq 0$ hoặc $m\geq 28$

• B. m <0 hoặc m>28

• C. 0<m<28
• D. m>0

Câu 7: Số giá trị nguyên của x để tam thức f(x)=2x$^{2}$−7x−9 nhận giá trị âm là

• A. 3

• B. 4
• C. 5
• D. 6

Câu 8: Tìm tất cả các giá trị của tham số m sao cho tam thức bậc hai $(m-1)x^{2}+(3m-2)x+3-2m=0$ đổi dấu hai lần trên R?

• A. $m\in R$

• B. $m\neq 1$

• C. $m\neq -1$
• D. -1<m<2

Câu 9: Cho $f(x)=-2x^{2}+(m+2)x+m-4$. Tìm m để f(x) âm với mọi x.

• A. $x\in (-2;4)$
• B. $m\in [-14;2]$

• C. $m\in (-14;2)$

• D. $m\in [-4;2]$

Câu 10: Cho f(x)=ax$^{2}$+bx+c(a≠0)có $Δ=b^{2}−4ac<0$. Khi đó mệnh đề nào đúng?

• A. f(x)>0,∀x∈R
• B. f(x)<0,∀x∈R

• C. f(x) không đổi dấu;

• D. Tồn tại x để f(x)=0

Câu 11: Tam thức bậc hai $f(x)=x^{2}+(1-\sqrt{3})x-8-5\sqrt{3}$

• A. Dương với mọi x∈R
• B. Âm với mọi x∈R

• C. Âm với mọi x∈$(-2-\sqrt{3};1+2\sqrt{3})$

• D. Âm với mọi x∈(−∞;1)

Câu 12: Cho f(x)=ax$^{2}$+bx+c(a≠0). Điều kiện để f(x)≥0,∀x∈R là

• A. $\left\{\begin{matrix}a>0\\ \Delta \leq 0\end{matrix}\right.$

• B. $\left\{\begin{matrix}a>0\\ \Delta \geq 0\end{matrix}\right.$
• C. $\left\{\begin{matrix}a>0\\ \Delta < 0\end{matrix}\right.$
• D. $\left\{\begin{matrix}a<0\\ \Delta > 0\end{matrix}\right.$

Câu 13: Cho các tam thức f(x)=2x$^{2}$−3x+4;g(x)=−x$^{2}$+3x−4;h(x)=4−3x$^{2}$. Số tam thức đổi dấu trên R là:

• A. 0 ;

• B. 1 ;

• C. 2. ;
• D. 3.

Câu 14: Cho f(x)=x$^{2}$−4x+3. Trong các mệnh đề sau, mệnh đề đúng là:

• A. f(x)<0,∀x∈(−∞;1)∪(3;+∞);

• B. f(x)≤0,∀x∈(1;3);

• C. f(x)≥0,∀x∈(−∞;1)∪(3;+∞);
• D. f(x)>0,∀x∈(1;3).

Câu 15: Tam thức bậc hai f(x)=2x$^{2}$+2x+5 nhận giá trị dương khi và chỉ khi

• A. x∈(0;+∞)
• B. x∈(−2;+∞)

• C. x∈R

• D. x∈(−∞;2).

Câu 16:  Cho f(x)=ax$^{2}$+bx+c(a≠0). Điều kiện để f(x)≤0,∀x∈R là

• A. $\left\{\begin{matrix}a<0\\ \Delta \leq 0\end{matrix}\right.$

• B. $\left\{\begin{matrix}a<0\\ \Delta \geq 0\end{matrix}\right.$
• C. $\left\{\begin{matrix}a>0\\ \Delta < 0\end{matrix}\right.$
• D. $\left\{\begin{matrix}a<0\\ \Delta < 0\end{matrix}\right.$

Câu 17: Bảng xét dấu nào sau đây là của tam thức $f(x)=x^{2}+12x+36$?

• A.
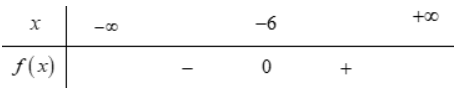
• B. 

• C. 

• D. 

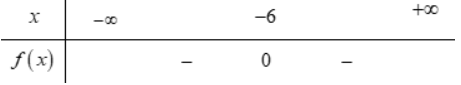
Câu 18: Cho tam thức bậc hai $f(x)=x^{2}-bx+3$. Với giá trị nào của b thì tam thức f(x) có hai nghiệm phân biệt?

• A. $b\in[-2\sqrt{3};2\sqrt{3}]$
• B. $b\in (-2\sqrt{3};2\sqrt{3})$
• C. $b\in (-\infty ;-2\sqrt{3}]\cup [2\sqrt{3};+\infty )$

• D. $b\in (-\infty ;2\sqrt{3})\cup (2\sqrt{3};+\infty )$

Câu 19: cho phương trình $x^{2}+2x-m^{2}=0$. Biết rằng có hai giá trị m1, m2 của tham số m để phương trình có hai nghiệm x1, x2 thỏa mãn $x_{1}^{3}+x_{2}^{3}+10=0$. Tính $m1\times m2$

• A. $\frac{3}{4}$

• B. $-\frac{1}{3}$

• C. $-\frac{3}{4}$
• D. $\frac{1}{3}$

Câu 20: Cho f(x)=ax$^{2}$+bx+c(a≠0). Điều kiện để f(x)>0,∀x∈R là

• A. $\left\{\begin{matrix}a<0\\ \Delta \leq 0\end{matrix}\right.$
• B. $\left\{\begin{matrix}a<0\\ \Delta \geq 0\end{matrix}\right.$
• C. $\left\{\begin{matrix}a>0\\ \Delta < 0\end{matrix}\right.$

• D. $\left\{\begin{matrix}a<0\\ \Delta < 0\end{matrix}\right.$