I. DẤU CỦA TAM THỨC BẬC HAI 

HĐ1:

a. 

Từ hình 17 ta thấy parabol nằm hoàn toàn phía trên trục hoành nên tam thức bậc hai $f(x) = x^2 – 2x + 2 > 0$ với mọi $x \in R$.

b. 

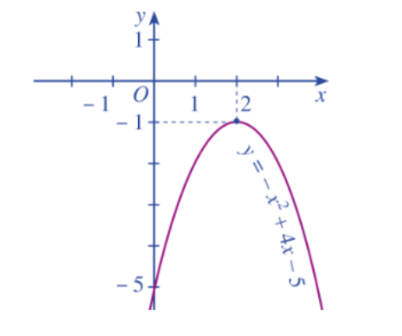
Từ hình ta thấy parabol nằm hoàn toàn phía dưới trục hoành nên tam thức bậc hai $f(x) = -x^2 + 4x – 5 < 0$ với mọi $x \in R$.  

c. Nếu $∆ < 0$ thì f(x) cùng dấu với hệ số a với mọi $x \in R$.

Nhận xét: 

Nếu $∆ < 0$ thì f(x) cùng dấu với hệ số a với mọi $x \in R$.

HĐ2:

a.

Từ đồ thị ta thấy $x^2 + 2x + 1 > 0 ; \forall x \in R \setminus \begin{Bmatrix}-1\end{Bmatrix}$

b. 

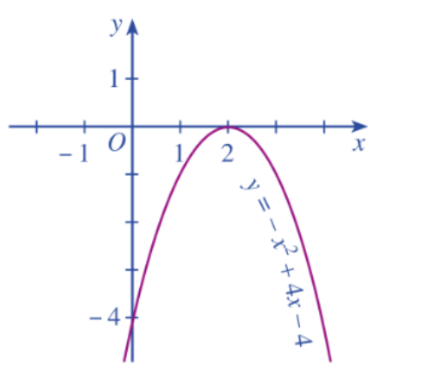
Từ đồ thị ta thấy $–x^2 + 4x – 4 < 0  \forall x \in R \setminus \begin{Bmatrix}
2
\end{Bmatrix}$

c. Nếu $∆ = 0$ thì f(x) cùng dấu với hệ số a với $\forall x \in R \setminus \begin{Bmatrix}
\frac{-b}{2a}
\end{Bmatrix}$

Nhận xét: Nếu $∆ = 0$ thì f(x) cùng dấu với hệ số a với $\forall x \in R \setminus \begin{Bmatrix}
\frac{-b}{2a}
\end{Bmatrix}$

HĐ3:

a. 

Ta thấy: 

+ Trên các khoảng $(-\infty;2)$ và $(-1;+\infty)$ phần parabol nằm hoàn toàn phía trên trục hoành nên tam thức bậc hai $f(x) = x^2 +3x + 2 > 0$ 

+ Trên khoảng (-2;-1) phần parabol nằm hoàn toàn phía dưới trục hoành nên tam thức bậc hai $f(x) = x^2 +3x + 2 < 0$ 

b. 

Ta thấy: 

+ Trên các khoảng $(-\infty;1)$ và $(3;+\infty)$ phần parabol nằm hoàn toàn phía dưới trục hoành nên tam thức bậc hai $f(x) = x^2 + 4x – 3 < 0$ 

+ Trên khoảng $(1;3)$ phần parabol nằm hoàn toàn phía trên trục hoành nên tam thức bậc hai $f(x) = x^2 + 4x – 3 > 0$

c. Nếu $∆ > 0$ thì f(x) cùng dấu với hệ số a với mọi x thuộc các khoảng $(-\infty;x_1)$ và $(x_2;+\infty)$; $f(x)$ trái dấu với hệ số a với mọi x thuộc khoảng $(x_1; x_2)$, trong đó $x_1, x_2$ là hai nghiệm của $f(x)$ và $x_1 < x_2$. 

Nhận xét: 

Nếu $∆ > 0$ thì f(x) cùng dấu với hệ số a với mọi x thuộc các khoảng $(-\infty;x_1)$ và $(x_2;+\infty)$; f(x) trái dấu với hệ số a với mọi x thuộc khoảng $(x_1;x_2)$, trong đó $x_1, x_2$ là hai nghiệm của $f(x)$ và $x_1 < x_2$. 

Kết luận: 

Cho tam thức bậc hai $f(x) = ax^2 + bx + c (a \neq 0), ∆ = b^2 – 4ac$.

+ Nếu $∆ < 0$ thì f(x) cùng dấu với hệ số a với mọi $x \in R$. 

+ Nếu $∆ = 0$ thì f(x) cùng dấu với hệ số a $\forall x \in R \setminus \begin{Bmatrix}
\frac{-b}{2a}
\end{Bmatrix}$

+ Nếu $∆ > 0$ thì f(x) có hai nghiệm $x_1, x_2 (x_1 < x_2)$. Khi đó: 

f(x) cùng dấu với hệ số a với mọi x thuộc các khoảng $(-\infty;x_1)$ và $(x_2;+\infty)$; f(x) trái dấu với hệ số a với mọi x thuộc khoảng $(x_1;x_2)$.

Nhận xét: 

Trong định lí, có thể thay biệt thức $∆ = b^2 – 4ac$ bằng biệt thức thu gọn $∆’ = (b’)^2 – ac$ với $b = 2b’$

II. VÍ DỤ

Ví dụ 1 (SGK – tr46) 

Luyện tập 1:

a. $f(x) = -2x^2 + 4x -5$.

Ta có: $∆ = -24 < 0, a = -2 < 0$ nên $f(x) < 0$ với $\forall x \in R$.

b. $f(x) = -x^2 + 6x – 9$.

Ta có: $∆ = 0, a = -1 < 0$ nên $f(x) < 0$ với $ \forall x \in R \setminus \begin{Bmatrix}
3
\end{Bmatrix}$

Ví dụ 2 (SGK – tr46)

Luyện tập 2: 

Xét tam thức bậc hai $f(x) = - x^2 – 2x + 8$ có hai nghiệm phân biệt $x_1 = -4, x_2 = 2$ và hệ số $a = -1 < 0$. 

Ta có bảng xét dấu: