BÀI 12. MỘT SỐ HỆ THỨC GIỮA CẠNH, GÓC TRONG TAM GIÁC VUÔNG VÀ ỨNG 

DỤNG

MỞ ĐẦU

Để đo chiều cao của một toà lâu đài (H.4.11), người ta đặt giác kế thẳng đứng tại điểm M. Quay ống ngắm của giác kế sao cho nhìn thấy đỉnh P’ của toà lâu đài dưới góc nhọn α. Sau đó, đặt giác kể thẳng đứng tại điểm N, NM = 20 m, thì nhìn thấy đỉnh P’ dưới góc nhọn β (β < α). Biết chiều cao giác kế là 1,6 m, jayx tính chiều cao của toà lâu đài.

Giải nhanh:

Xét ∆M’P’H vuông tại H, theo định lí 2, ta có: M’H = P’H.cotα.

Xét ∆N’P’H vuông tại H, theo định lí 2, ta có: N’H = P’H.cotβ.

Mà N’H = N’M’ + M’H = MN + M’H

Do đó P’H.cotβ = MN + P’H.cotα.

Suy ra P’H.(cotβ – cotα) = MN nên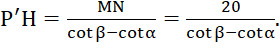

=> P’P = P’H + HP = 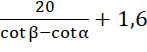(m).

1. HỆ THỨC GIỮA CẠNH HUYỀN VÀ CẠNH GÓC VUÔNG

Giải nhanh hoạt động 1 trang 74 sgk toán 9 tập 1 kntt

Cho tam giác ABC vuông tại A, cạnh huyền a và các cạnh góc vuông b, c (H.4.12).

a) Viết các tỉ số lượng giác sin, côsin của góc B và góc C theo độ dài các cạnh của tam giác ABC.

b) Tính mỗi cạnh góc vuông b và c theo cạnh huyền a và các tỉ số lượng giác trên của góc B và góc C.

Giải nhanh:

a) Ta có: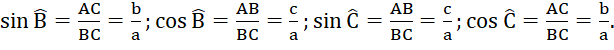

b) Ta có: 

+

+

Giải nhanh luyện tập 1 trang 75 sgk toán 9 tập 1 kntt

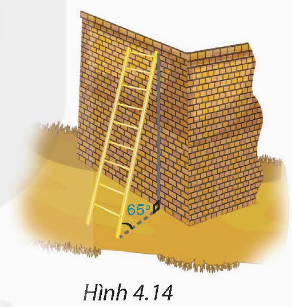
1. Một chiếc thang dài 3 m. Cần đặt chân thang cách chân tường một khoảng bằng bao nhiêu mét (làm tròn đến chữ số thập phân thứ hai) để nó tạo được với mặt đất một góc “an toàn” 65^o (tức là đảm bảo thang chắc chắn khi sử dụng) (H.4.14)?

2. Một khúc sông rộng khoảng 250 m. Một con đò chèo qua sông bị dòng nước đẩy xiên nên phải chèo khoảng 320 m mới sang được bờ bên kia. Hỏi dòng nước đã đẩy con đò đi lệch một góc α bằng bao nhiêu độ (làm tròn đến phút)? (H.4.15).

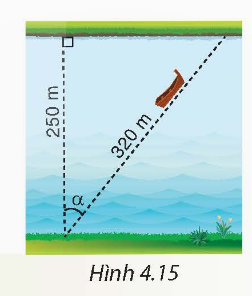
Giải nhanh:

1. Giả sử BC là độ dài thang và AB là khoảng cách từ chân thang đến chân tường.

Xét ∆ABC vuông tại A, ta có: AB = BC×cosB = 3×cos65° ≈ 1,27 (m).

Vậy cần đặt chân thang cách chân tường một khoảng 1,27 m để bó tạo được với mặt đất một góc “an toàn” 65°.

2. Dòng nước đã đẩy chiếc đò lệch đi một góc là:

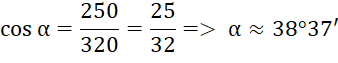
2. HỆ THỨC GIỮA HAI CẠNH GÓC VUÔNG

Giải nhanh hoạt động 2 trang 75 sgk toán 9 kết nối tri thức và cuộc sống

Xét tam giác ABC trong Hình 4.16.

a) Viết các tỉ lệ lượng giác tang, côtang của góc B và góc C theo b, c.

b) Tính mỗi cạnh góc vuông b và c theo cạnh góc vuông kia và các tỉ số lượng giác trên của góc B và góc C.

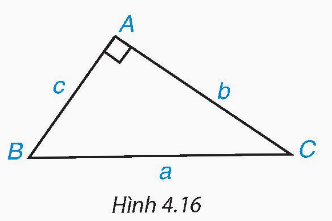
Giải nhanh:

a) Ta có: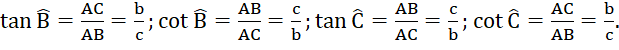

b) Ta có: 

+

+

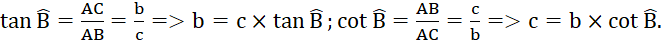
Giải nhanh luyện tập 2 trang 76 sgk toán 9 tập 1 kntt

Bóng trên mặt đất của một cây dài 25 m. Tính chiều cao của cây (làm tròn đến dm), biết rằng tia nắng mặt trời tạo với mặt đất góc 40^o (H.4.18).

Giải nhanh:

Ta nhận thấy chiều cao h của cây đối diện với góc 40° (góc tạo bởi tia nắng mặt trời và bóng của cây trên mặt đất).

Theo Định lí 2, ta có h = 25.tan40° ≈ 20,9775 (m) = 209,775 (dm) ≈ 210 (dm).

Vậy chiều cao của tháp là khoảng 210 dm.

3. GIẢI TAM GIÁC VUÔNG

Giải nhanh luyện tập 3 trang 77 sgk toán 9 tập 1 kntt

Cho tam giác ABC vuông tại A có AB = 3, cạnh huyền BC = 8. Tính cạnh AC (làm tròn đến chữ số thập phân thứ ba) và các góc B, C (làm tròn đến độ).

Giải nhanh:

Theo định lí Pythagore, có AC² = BC² – AB² = 8² – 4² = 48 nên AC = 6,928.

Ta có .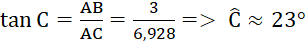

Suy ra .

Giải nhanh câu hỏi trang 77 sgk toán 9 tập 1 kntt

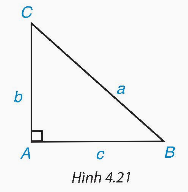
1. Hãy nêu cách giải tam giác ABC vuông tại A khi biết hai cạnh AB = c, AC = b hoặc AB = c, BC = a và không sử dụng định lí Pythagore (H.4.21).

2. Hãy nêu cách giải tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.

Giải nhanh:

1.  Trường hợp biết AB = c, AC = b

Tam giác ABC vuông tại A nên ta có: 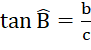từ đó ta tính được góc B, và tính được góc C thông qua định lý tổng ba góc trong một tam giác. Sau khi tính được góc B, ta dùng tỉ số lượng giác từ đó ta tính được

Trường hợp AB = c, BC = a

Tam giác ABC vuông tại A nên ta có: 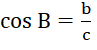từ đó ta tính được góc B, và tính được góc C thông qua định lý tổng ba góc trong một tam giác. Sau khi tính được góc B, ta dùng tỉ số lượng giác từ đó ta tính được AC = c×tan B

2. Tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.

Trường hợp biết cạnh góc vuông AB và góc B

Biết góc B ta tính được góc C thông qua định lý tổng ba góc trong một tam giác. Để tính cạnh BC ta dùng tỉ số lượng giác từ đó ta tính được và tỉ số lượng giác 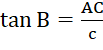=> AC = c×tan B 

Trường hợp biết cạnh huyền BC và góc B

Biết góc B ta tính được góc C thông qua định lý tổng ba góc trong một tam giác. Để tính cạnh AB ta dùng tỉ số lượng giác 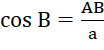từ đó ta tính được 

AB = a×cos B và tỉ số lượng giác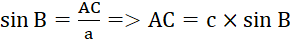

Giải nhanh luyện tập 4 trang 77 sgk toán 9 tập 1 kết nối tri thức

Giải tam giác ABC vuông tại A, biết BC = 9,

Giải nhanh:

Ta có: sin C = => AB = 9×sin 53^o = 7,19.

cos C = => AC = 9×cos 53^o = 5,42.

Giải nhanh vận dụng trang 77 sgk toán 9 tập 1 kntt

Giải bài toán ở tình huống mở đầu với α = 27^o và β = 19^o.

Giải nhanh:

Xét ∆M’P’H vuông tại H, theo định lí 2, ta có: M’H = P’H.cotα.

Xét ∆N’P’H vuông tại H, theo định lí 2, ta có: N’H = P’H.cotβ.

Mà N’H = N’M’ + M’H = MN + M’H

Do đó P’H.cotβ = MN + P’H.cotα.

=>  P’H.(cotβ – cotα) = MN nên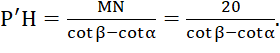

=> P’P = P’H + HP = 22,84 m.

4. GIẢI NHANH BÀI TẬP CUỐI SGK

Giải nhanh bài 4.8 trang 78 sgk toán 9 tập 1 kntt

Giải tam giác ABC vuông tại A có BC = a, AC = b, AB = c, trong các trường hợp:

a) a = 21, b = 18;             b) b = 10, ;                   c) c = 5, b = 3.

Giải nhanh:

a) Áp dụng định lí Pythagore:  

Ta có: sin C =

b) Ta có: cos C =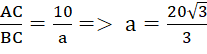

sin C =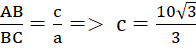

c) Áp dụng định lí Pythagore:  

Ta có: sin C =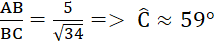

Giải nhanh bài 4.9 sgk trang 78 toán 9 tập 1 kết nối tri thức và cuộc sống

Tính góc nghiêng α của thùng xe chở rác trong Hình 4.22.

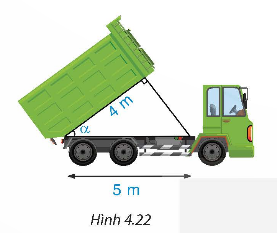
Giải nhanh:

Ta có: cos α  

Giải nhanh bài 4.10 trang 78 sgk toán 9 tập 1 kết nối tri thức và cuộc sống

Tìm góc nghiêng α và chiều rộng AB của mái nhà kho trong Hình 4.23.

Giải nhanh:

Ta có: tan α = => α = 3,43^o 

Giải nhanh bài 4.11 trang 78 sgk toán 9 tập 1 kết nối tri thức và cuộc sống

Tính các góc của hình thoi có hai đường chéo dài và 2. 

Giải nhanh:

Vì O là trung điểm BD và AC nên BO =1; AO = .

Ta có:

Vì AC là phân giác của góc BAD nên

=>

Giải nhanh bài 4.12 trang 78 sgk toán 9 tập 1 kết nối tri thức và cuộc sống

Cho hình thang ABCD (AD//BC) có AD = 16 cm, BC = 4 cm và

a) Kẻ đường cao CE của tam giác ACD. Chứng minh Rính sin của các góc và suy ra AC² = AE . AD. Từ đó tính AC.

b) Tính góc D của hình thang.

Giải nhanh:

a) Ta có:
nên

Ta có: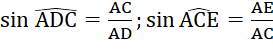

=>

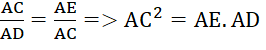
Hình thang ABCD có AD//BC và AB BC (do ) nên AB AD.

Tứ giác ABCE có nên ABCE là hình chữ nhật.

=> AE = BC = 4 cm (tính chất hình chữ nhật)

=> AC² = 4×16 = 64 nên AC = 8 cm

sin D = .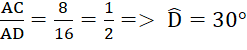

Giải nhanh bài 4.13 trang 78 sgk toán 9 tập 1 kết nối tri thức và cuộc sống

Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình ảnh phản chiếu qua gương B của ngọn cây (cây có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tính chiều cao của cây (H.4.24).

Giải nhanh:

Ta có:

CE = Bc.tan

Vậy chiều cao của cây là 6,6 m.