BÀI TẬP CUỐI CHƯƠNG IX

A. TRẮC NGHIỆM

Giải nhanh bài 9.37 trang 92 sgk toán 9 tập 2 kntt

Khẳng định nào sau đây là đúng?

A.Góc nội tiếp có số đo bằng số đo cung bị chắn.

B.Góc có hai cạnh chứa các dây cung của đường tròn là góc nội tiếp đường tròn đó.

C.Góc nội tiếp có số đo bằng một nửa số đo cung bị chắn.

D.Góc có đỉnh nằm trên đường tròn là góc nội tiếp đường tròn đó.

Giải nhanh:

Chọn đáp án C

Giải nhanh bài 9.38 trang 92 sgk toán 9 tập 2 kntt

Cho tứ giác ABCD nội tiếp một đường tròn có 

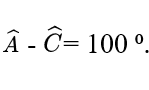
Khẳng định nào dưới đây là đúng?

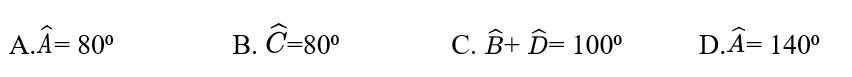
Giải nhanh:

Chọn đáp án D

Giải nhanh bài 9.39 trang 92 sgk toán 9 tập 2 kntt

Đa giác nào dưới đây không nội tiếp một đường tròn?

A.Đa giác đều                                            B.Hình chữ nhật

C.Hình bình hành                                        D.Tam giác

Giải nhanh:

Chọn đáp án C

B. TỰ LUẬN

Giải nhanh bài 9.40 trang 92 sgk toán 9 tập 2 kntt

Cho tam giác ABC có các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC và I là trung điểm của AH. Chứng minh rắng:

a)Tứ giác AEHF nội tiếp đường tròn tâm I;

b)ME, MF tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.

Giải nhanh:

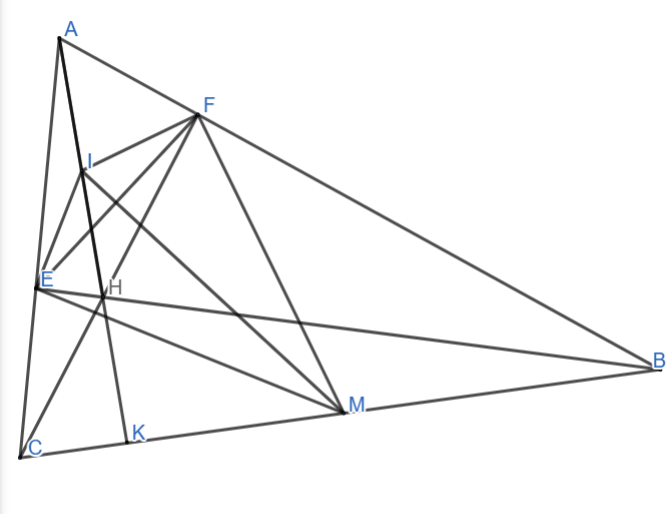
a) Xét tứ giác AEHF có 

∠AEH=∠AFH=90ᵒ(BE và CF là hai đường cao tương ứng)

=>Tứ giác AEHF nội tiếp đường tròn tâm I

b)Kéo dài AH cắt BC tại K

=>AH ⊥BC tại K

Có ∠EBC+∠ECK=90ᵒ

∠KAC+∠ACK=90ᵒ

=>∠EBC=∠KAC

Do AI=AH=>∠KAC=∠AEI(tính chất trung tuyến trong tam giác vuông)

Do BM=ME=>∠EBC=∠BEM(tính chất trung tuyến trong tam giác vuông)

=>∠AEI+∠FEH=∠FEH+∠BEM

Hay ∠FEM=∠AEB=90ᵒ(dpcm)

Giải nhanh bài 9.41 trang 92 sgk toán 9 tập 2 kntt

Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng các tứ giác ANOP, BPOM, CMON là các tứ giác nội tiếp.

Giải nhanh:

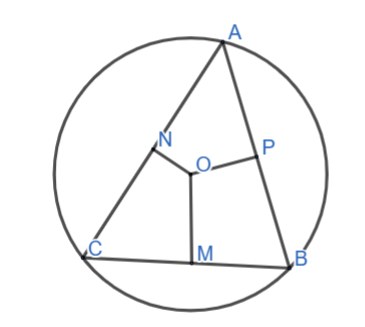
Tam giác ABC nội tiếp đường tròn (O) => O là giao điểm của ba đường trung trực của tam giác ABC.

Hay ON⊥AC; OP⊥AB; OM⊥BC

Xét tứ giác ANOP có 

∠ANO+∠APO=90+90=180ᵒ

=>Tứ giác ANOP nội tiếp 

Xét tứ giác BPOM có

∠BPO+∠BMO=90+90=180ᵒ

=>Tứ giác BPOM nội tiếp

Xét tứ giác CMON có

∠CMO+∠CNO=90+90=180ᵒ

=>Tứ giác CMON nội tiếp.

Giải nhanh bài 9.42 trang 92 sgk toán 9 tập 2 kntt

Cho một hình lục giác đều và một hình vuông cùng nội tiếp một đường tròn. Biết rằng hình vuông có cạnh bằng 3 cm.Tính chu vi và diện tích của một hình lục giác đều đã cho.

Giải nhanh:

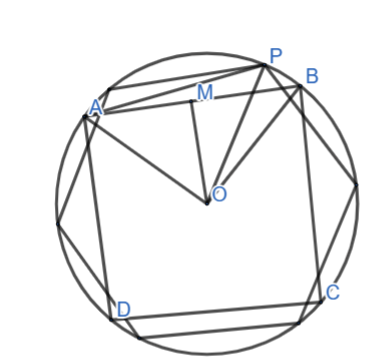
Gọi O là tâm đường tròn, AB là cạnh hình vuông, M là trung điểm AB.

Ta có OA=OB=R

Tam giác AOM vuông cân tại M(AM=OM=)

Do đó: R=OA=OM==1,5cm

Gọi P là 1 đỉnh của hình lục giác đều 

Nối OP và AP 

OP=R=1,5 cm

Tam giác AOP vuông cân tại M

=> AP=OA=OP=1,5cm

Chu vi hình lục giác đều C= 6.AP=6.1,5=9 cm

Diện tích hình vuông S==9

Diệc tích 6 tam giác đều AOP = 6..=27

Diện tích lục giác đều = diện tích hình vuông+ diện tích tam giác

=9+27=29,25

Vậy chu vi lục giác đều là 9 cm

Diện tich hình lục giác đều là 29,25

Giải nhanh bài 9.43 trang 92 sgk toán 9 tập 2 kntt

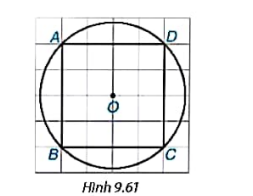
a, Phép quay thuận chiều 45 độ tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’ (H.9.61). Hãy vẽ tứ giác A’B’C’D’.

b, Phép quay trong câu  a biến các điểm A’, B’, C’, D’ thành những điểm nào?

Giải nhanh:

a)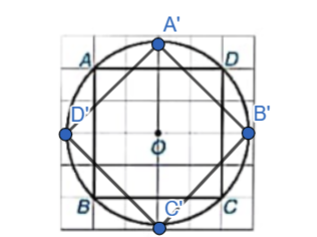

b) Phép quay trong câu  a biến các điểm A’, B’, C’, D’ thành những điểm : D,C,B,A.

Giải nhanh bài 9.44 trang 92 sgk toán 9 tập 2 kntt

Bạn Lam muốn cắt hình ngôi sao có dạng như Hình 9.62 (trong đó ABCDE là một ngũ giác đều). Lan gấp đôi tờ giấy, vẽ một nửa ngồi sao và cắt theo nét vẽ. Góc tạo bởi lưỡi kéo và nếp gấp lúc đầu bằng bao nhiêu?

Giải nhanh:

Góc tạo bởi lưỡi kéo và nếp gấp lúc đầu bằng 15 độ