Dễ hiểu giải Toán 9 Kết nối bài 18: Hàm số y = ax^2 (a ≠ 0)
Giải dễ hiểu bài 18: Hàm số y = ax^2 (a ≠ 0). Trình bày rất dễ hiểu, nên tiếp thu Toán 9 Kết nối tri thức dễ dàng. Học sinh nắm được kiến thức và biết suy rộng ra các bài tương tự. Thêm 1 dạng giải mới để mở rộng tư duy. Danh mục các bài giải trình bày phía dưới
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 18: HÀM SỐ Y=A
Mở đầu: Một cây cầu treo có trụ tháp đôi cao 75m so với mặt đất của cây cầu và cách nhau 400m. Các dây cáp có dạng đồ thị của hàm số y=a![]() (a
(a![]() như hình 6.1 và được treo trên các đỉnh tháp. Tìm chiều cao CH của dây cáp biết điểm H cách tâm O của cây cầu 100m (giả sử mặt của cây cầu là bằng phẳng).
như hình 6.1 và được treo trên các đỉnh tháp. Tìm chiều cao CH của dây cáp biết điểm H cách tâm O của cây cầu 100m (giả sử mặt của cây cầu là bằng phẳng).

Giải nhanh:


a)Sau 2 giây, vật rơi được quãng đường là: s= 4,9.![]() =19,6 m
=19,6 m
Vật cách mặt đất: 98-19,6=78,4 m
b) Vật chạm đất => 98=4,9![]() => t=4,5
=> t=4,5
Vậy sau 4,5 giây kể từ khi bắt đầu rơi, vật chạm đất.
2. ĐỒ THỊ CỦA HÀM SỐ Y=A
Giải nhanh hoạt động 3 trang 6 sgk toán 9 tập 2 kntt
Cho hàm số y=2![]() .
.
a)Hoàn thành bảng giá trị sau vào vở:

b)Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x;y) trong bảng giá trị ở câu a. Bằng cách tương tự, lấy nhiều điểm (x;2![]() ) với x
) với x![]() R và nối lại, ta được đồ thị của hàm số y=2
R và nối lại, ta được đồ thị của hàm số y=2![]() .
.
Giải nhanh:
a)
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
y | 18 | 8 | 2 | 0 | 2 | 8 | 18 |
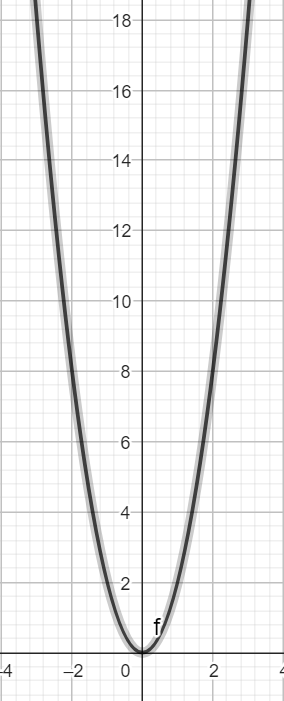
b)Gọi các điểm (x;y) ở câu a lần lượt là A(-3;18); B(-2.;8); C(-1;2); D(1;2); E(2;8) và F(3;18) ; O(0;0). Biểu diễn trên mặt phẳng tọa độ Oxy ta được:
Giải nhanh hoạt động 4 trang 6 sgk toán 9 tập 2 kntt
Xét đồ thị hàm số y=2![]() đã vẽ ở Giải nhanh hoạt động 3(H.6.3)
đã vẽ ở Giải nhanh hoạt động 3(H.6.3)
a)Đồ thị nằm phía trên hay phía dưới trục hoành? Điểm nào là điểm thấp nhất của đồ thị?
b)So sánh hoành độ và tung độ của các cặp điểm thuộc đồ thị A(1;2) và ![]() (-1;2); B(2;8) và
(-1;2); B(2;8) và ![]() (-2;8). Từ đồ thị hãy nhận xét mối liên hệ về vị trí giữa các cặp điểm nêu trên.
(-2;8). Từ đồ thị hãy nhận xét mối liên hệ về vị trí giữa các cặp điểm nêu trên.
c)Tìm điểm C có hoành độ x=![]() thuộc đồ thị. Xác định tọa độ của điểm
thuộc đồ thị. Xác định tọa độ của điểm ![]() đối xứng với điểm C qua trục tung Oy và cho biết điểm
đối xứng với điểm C qua trục tung Oy và cho biết điểm ![]() có thuộc đồ thị đã cho hay không.
có thuộc đồ thị đã cho hay không.

Giải nhanh:
a) Từ hình vẽ ta thấy đồ thị nằm phía trên trục hoành.
Điểm thấp nhất của đồ thị là O(0;0)
b) -Hoành độ của các điểm A(1;2) và ![]() (-1;2); B(2;8) và
(-1;2); B(2;8) và ![]() (-2;8) đối xứng nhau qua trục Oy.
(-2;8) đối xứng nhau qua trục Oy.
- Tung độ của các điểm A(1;2) và ![]() (-1;2) là bằng nhau;tương tự tung độ của B(2;8) và
(-1;2) là bằng nhau;tương tự tung độ của B(2;8) và ![]() (-2;8) cũng bằng nhau.
(-2;8) cũng bằng nhau.
=>Các cặp điểm A(1;2) và ![]() (-1;2) đối xứng nhau qua trục Oy;
(-1;2) đối xứng nhau qua trục Oy;
B(2;8) và ![]() (-2;8) cũng đối xứng nhau qua trục Oy.
(-2;8) cũng đối xứng nhau qua trục Oy.
c)- Điểm C có hoành độ x=![]() thuộc đồ thị=> y=2.(
thuộc đồ thị=> y=2.(![]() =
=![]()
=>C(![]() ;
;![]() )
)
-Điểm ![]() đối xứng với điểm C qua trục tung Oy=> tung độ của điểm
đối xứng với điểm C qua trục tung Oy=> tung độ của điểm ![]() cũng là
cũng là ![]() , và hoành độ của điểm
, và hoành độ của điểm ![]() là -
là - ![]()
=>![]() (
(![]() ;
;![]() )
)
Thay tọa độ điểm ![]() (-
(-![]() ;
;![]() ) vào đồ thị hàm số y=2
) vào đồ thị hàm số y=2![]() ta được:
ta được:
![]() =2.(
=2.(![]()
Vế trái bằng vế phải=> điểm ![]() có thuộc đồ thị y=2
có thuộc đồ thị y=2![]()
Giải nhanh luyện tập 2 trang 8 sgk toán 9 tập 2 kntt
Vẽ đồ thị của hàm số y=![]() . Tìm các điểm thuộc đồ thị có tung độ bằng 2 và nhận xét về tính đối xứng giữa các điểm đó.
. Tìm các điểm thuộc đồ thị có tung độ bằng 2 và nhận xét về tính đối xứng giữa các điểm đó.
Giải nhanh:
x | -2 | -1 | 0 | 1 | 2 |
y | 2 |
| 0 |
| 2 |

Các điểm thuộc đồ thị có tung độ bằng 2 là A(-2;2) và D(2;2). Chúng đối xững với nhau qua trục Oy.
Giải nhanh vận dụng 2 trang 8 sgk toán 9 tập 2 kntt
Giải quyết bài toán ở tình huống mở đầu.

Giải nhanh:
Các dây cáp có dạng của đồ thị hàm số y=a![]() (a
(a![]() .
.
Từ hình vẽ ta thấy B(200;75) thuộc đồ thị hàm số y=a![]() (a
(a![]() , thay vào đồ thị ta được:
, thay vào đồ thị ta được:
75=a.![]() => a=0,001875
=> a=0,001875
Vậy đồ thị hàm số của các dây cáp là y=0,001875![]()
Từ đồ thị ta thấy điểm C ![]() đồ thị , mà C có hoành độ là 100
đồ thị , mà C có hoành độ là 100
=> y=0,001875.![]() = 18,75
= 18,75
Vậy chiều cao CH là 18,75 m
3. GIẢI NHANH BÀI TẬP CUỐI SGK
Giải nhanh bài 6.1 trang 8 sgk toán 9 tập 2 kntt
Cho hàm số y=0,25![]() . Hoàn thành bảng giá trị sau vào vở:
. Hoàn thành bảng giá trị sau vào vở:

Giải nhanh:
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
y | 2,25 | 1 | 0,25 | 0 | 0,25 | 1 | 2,25 |
Giải nhanh bài 6.2 trang 8 sgk toán 9 tập 2 kntt
Cho hình lăng trụ đứng có đáy là hình vuông cạnh a(cm) và chiều cao 10cm.
a)Viết công thức tính thể tích V của lăng trụ theo a và tính giá trị của V khi a=2cm.
b)Nếu dộ dài cạnh đáy tăng lên hai lần thì thể tích của hình lăng trụ thay đổi thế nào?
Giải nhanh:
a) Khi a =2cm=> V=![]() .10 =40 cm
.10 =40 cm
b) V=![]() .10=4.
.10=4.![]() .10
.10
=>Thể tích của hình lăng trụ sẽ tăng 4 lần so với ban đầu.
Giải nhanh bài 6.3 trang 8 sgk toán 9 tập 2 kntt
Diện tích toàn phần S(![]() của hình lập phương,tức là tổng diện tích xung quanh và diện tích của hai mặt đáy là một hàm số của độ dài cạnh a(cm).
của hình lập phương,tức là tổng diện tích xung quanh và diện tích của hai mặt đáy là một hàm số của độ dài cạnh a(cm).
a)Viết công thức của hàm số này.
b)Sử dụng công thức nhận được ở câu a để tính độ dài cạnh của một hình lập phương có diện tích toàn phần là 54 ![]() .
.
Giải nhanh:
a) S=6![]()
b) Hình lập phương có diện tích toàn phần là 54 ![]() =>a=3 cm
=>a=3 cm
Giải nhanh bài 6.4 trang 8 sgk toán 9 tập 2 kntt
Vẽ đồ thị của các hàm số sau:
a)y=3![]()
b)y=![]()
Giải nhanh:
a)
x | -2 | -1 | 0 | 1 | 2 |
y | 12 | 3 | 0 | 3 | 12 |

b)
x | -2 | -1 | 0 | 1 | 2 |
y |
|
| 0 |
|
|

Giải nhanh bài 6.5 trang 8 sgk toán 9 tập 2 kntt
Biết rằng đường cong trong hình 6,6 là một parabol y=a![]()
a)Tìm hệ số a
b)Tìm tung độ của điểm thuộc parabol có hoành độ x=-2
c)Tìm các điểm thuộc parabol có tung độ y=8.

Giải nhanh:
a)Từ đồ thị ta thấy (2;2) thuộc đồ thị hàm số y=a![]()
=> 2=a.![]() =>a=
=>a=![]()
b) Điểm thuộc parabol có hoành độ x=-2
=>y=![]() =2
=2
Vậy tung độ của điểm thuộc parabol có hoành độ x=-2 là y=2.
c) Các điểm thuộc parabol có tung độ y=8=> 8=![]() =>x=
=>x=![]()
Vậy điểm (4;8) và (-4;8) thuộc đồ thị.
Giải nhanh bài 6.6 trang 9 sgk toán 9 tập 2 kntt
Trong hình 6.7 có hai đường cong là đồ thị của hai hàm số y=-3![]() và y=
và y=![]() . Hãy cho biết đường nào là đồ thị của hàm số y=-3
. Hãy cho biết đường nào là đồ thị của hàm số y=-3![]() .
.
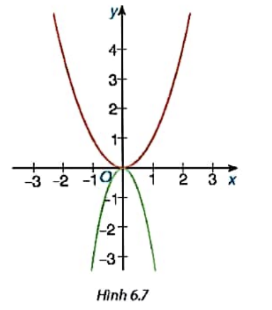
Giải nhanh:
Xét đồ thị của hàm số y=-3![]() , ta thấy hệ số a<0
, ta thấy hệ số a<0
=>Đồ thị sẽ ở dưới trục hoành hay đường màu đỏ sẽ là đồ thị của y=-3![]()
Giải nhanh bài 6.7 trang 9 sgk toán 9 tập 2 kntt
Một cổng vòm được thiết kế dạng parabol y=a![]() như hình 6.8. Biết chiều rộng của chân cổng là AB=6m và chiều cao của cổng là OI=4,5m.
như hình 6.8. Biết chiều rộng của chân cổng là AB=6m và chiều cao của cổng là OI=4,5m.

a)Tìm hệ số a dựa vào các dữ kiện trên. Từ đó, tính độ dài đoạn HK biết H cách điểm chính giữa cổng I là 2m.
b)Để vận chuyển hàng qua cổng, người ta dự định sử dụng một xe tải có chiều rộng 2m, chiều cao 3m. Hỏi xe tải này có thể đi qua được cổng vòm đó hay không?
Giải nhanh:
a)*Từ đồ thị ta thấy B(3;-4,5) thuộc đồ thị
=>-4,5=a.![]() =>a=-0,5
=>a=-0,5
Vậy đồ thị hàm số có dạng y=-0,5![]()
* H cách điểm chính giữa cổng I là 2m=>K(2;y)
K thuộc đồ thị hàm số y=-0,5![]() => y=-0,5.
=> y=-0,5. ![]() =-2
=-2
Vậy K(2;-2); H(2;-4,5)
Độ dài HK là |-4,5|-|-2|=2,5 m
b)Ta có OI=4,5m; AB=6m
=> Một xe tải có chiều rộng 2m, chiều cao 3m có thể đi qua được cổng vòm.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

Bình luận