LUYÊN TẬP CHUNG

Giải chi tiết bài 9.31 trang 91 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho tam giác ABC có các đường cao AD,BE,CF. Chứng minh rằng BCEF, CAFD, ABDE là những tứ giác nội tiếp.

Giải chi tiết:

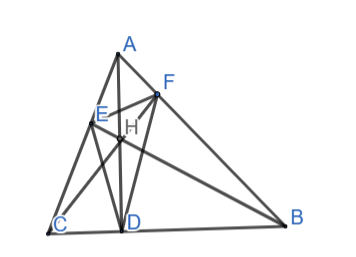
Xét tứ giác BCEF có

          ∠CEB = ∠CFB = 90ᵒ(CF, BE là 2 đường cao tương ứng) và cùng chắn cung BC.

 => BCEF nội tiếp đường tròn

Xét tứ giác CAFD có

∠AFC = ∠ADC(AD, CF là 2 đường cao tương ứng) và cùng chắn cung AC

 => CAFD nội tiếp đường tròn.

Xét tứ giác ABDE có

∠ADB = ∠AEB và cùng chắn cung AB

 => ABDE nội tiếp đường tròn.

Giải chi tiết bài 9.32 trang 91 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như hình 9.58. Biết và , tính số đo các góc của tứ giác ABCD.

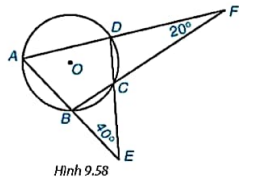
Giải chi tiết:

Ta có ∠A+∠E+∠ADE = 180ᵒ(tổng 3 góc trong 1 tam giác)

∠A+∠F+∠ABF = 180ᵒ(tổng ba góc trong 1 tam giác)

 => 2. ∠A+40+20+∠ADE+∠ABF = 360

< => 2∠A+∠ADE+∠ABF = 300

Mà ABCD nội tiếp đường tròn (O)

 => ∠ADE+∠ABF = 180ᵒ

 =>  2∠A+180 = 300

< => 2∠A = 120

< => ∠A = 60ᵒ

Tứ giác ABCD nội tiếp  => ∠DCB = 180-∠A = 180-60 = 120ᵒ

Có ∠DCB = 120 ᵒ =>  ∠DCF = 180-120 = 60ᵒ(hai góc ở vị trí kề bù)

Ta lại có ∠CDF = 180-∠DCF-∠F(tổng 3 góc trong một tam giác)

 => ∠CDF = 180-60-20 = 100ᵒ

Mà ∠CDF và ∠CDA là hai góc kề bù => ∠CDA = 180-100 = 80ᵒ

Tứ giác ABCD nội tiếp => ∠CDA+∠CBA = 180ᵒ

 => ∠CBA = 180-80 = 100ᵒ

Vậy ∠CBA = 100ᵒ; ∠CDA = 80ᵒ; ∠A = 60ᵒ; ∠DCB = 120ᵒ

Giải chi tiết bài 9.33 trang 91 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho hình vuông ABCD có cạnh bằng 4cm. Tính chu vi, diện tích của các đường tròn nội tiếp và ngoại tiếp hình vuông ABCD.

Giải chi tiết:

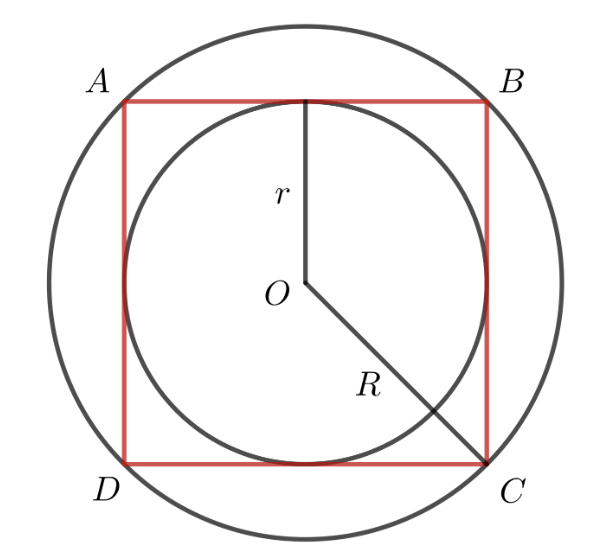
Gọi r là bán kính đường tròn nội tiếp hình vuông ABCD

R là bán kính đường tròn ngoại tiếp hình vuông ABCD

*Ta có r = = 2 cm

Chu vi đường tròn nội tiếp hình vuông ABCD là 2.2.3,14 = 12,56 cm

Diện tích đường tròn nội tiếp hình vuông ABCD là

* Ta có R = = 2 cm

Chu vi đường tròn ngoại tiếp hình vuông ABCD là 2.2.3,14 = 17,76 cm

Diện tích đường tròn ngoại tiếp hình vuông ABCD là

Giải chi tiết bài 9.34 trang 91 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Biết rằng 4 đỉnh A,B,C,D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều kim đồng hồ. Phép quay thuận chiều 45ᵒ biến các điểm A,B,C,D lần lượt thành các điểm E,F,G,H.

a) Vẽ đa giác EAFBGCHD.

b) Đa giác EAFBGCHD có phải là một bát giác đều không? Vì sao?

Giải chi tiết:

a)

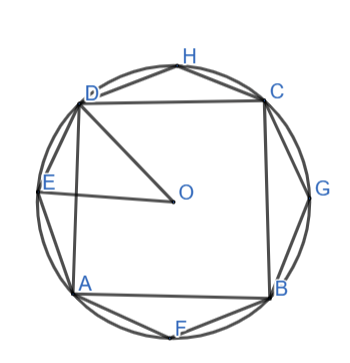
b) Ta có ABCD là hình vuông =>  Số đo các cung nhỏ AB, BC, CD, DA bằng 90ᵒ

Phép quay thuận chiều 45ᵒ biến các điểm A,B,C,D lần lượt thành các điểm E,F,G,H => Số đo các cung nhỏ AF, FB, BG, GC, CH, HD, DE, EA đều bằng 45ᵒ

 =>  AF = FB = BG = GC = CH = HD = DE = EA

 =>  AFBGCHDE là hình bát giác đều.

Giải chi tiết bài 9.35 trang 91 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

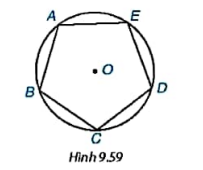
Cho ngũ giác đều ABCDE nội tiếp đường tròn (O) như hình 9.59.

a) Hãy tìm một phép quay thuận chiều tâm O biến điểm A thành điểm C.

b) Phép quay trên sẽ biến các điểm B,C,D,E lần lượt thành những điểm nào? Phép quay này có giữ nguyên ngũ giác đều ABCDE không?

Giải chi tiết:

a)Mỗi góc của ngũ giác đều là 108ᵒ

 Ta có ∠BAE = 108 = sd cung lớn BE

 => sd cung lớn BE =  216ᵒ

 =>  góc lớn BOE = sd cung lớn BE  = 216ᵒ

Mà ∠BOC+∠COD+∠DOE = 216ᵒ và ∠BOC = ∠COD = ∠DOE

 => ∠BOC = ∠COD = ∠DOE = 216:3 = 72ᵒ

Phép quay thuận chiều tâm O biến điểm A thành điểm C là phép quay tâm O với góc quay 72.3 = 216ᵒ

b)- Phép quay trên sẽ biến các điểm B,C,D,E lần lượt thành những điểm: D, E, A, B

- Phép quay này có giữ nguyên ngũ giác đều ABCDE.

Giải chi tiết bài 9.36 trang 91 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

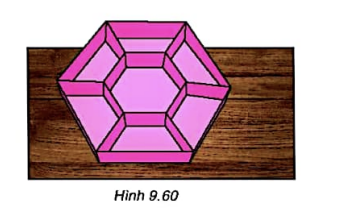
Người ta muốn làm một khay đựng bánh kẹo hình lục giác đều có cạnh 10 cm và chia thành 7 ngăn gồm một lục giác đều nhỏ và 6 hình thang cân như hình 9.60. Hỏi lục giác đều nhỏ phải có cạnh bằng bao nhiêu  để nó có diện tích bằng hai lần diện tích mỗi hình thang?

Giải chi tiết:

Gọi cạnh lục giác nhỏ là a cm

Diện tích lục giác đều nhỏ  = .tan() =

Chiều cao hình thang cân bằng cạnh lục giác đều lơn 10 cm

Gọi đường cao hạ từ đỉnh A của hình thang cân xuống đáy BC là h cm

Diện tích hình thang cân = (AB+CD). = (10+a).

Theo đề bài, diện tích lục giác đều nhỏ gấp hai lần diện tích mỗi hình thang cân

 =>

Khay đựng bánh kẹo được chia thành 7 phần bằng nhau, 1 phần là diện tích lục giác đều nhỏ và 6 phần là diện tích 6 hình thang cân.

Diện tích khay =  6. (10+a).+

Diện tích khay cũng bằng diện tích lục giác đều lớn 

Thay vào phương trình diện tích khay ta có 

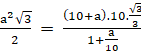
< => 3 = 100+10a+

Giải phương trình ta tìm được a = 5 cm

Vậy cạnh của lục giác đều nhỏ phải bằng 5cm để diện tich của nó bằng hai lần diện tích mỗi hình thang.