BÀI TẬP CUỐI CHƯƠNG II

A. TRẮC NGHIỆM

Giải nhanh bài 2.21 trang 42 sgk toán 9 tập 1 kntt

Nghiệm của bất phương trình -2x + 1 < 0 là

A.           B. x >              C.                   D.

Giải nhanh:

Đáp án B

Giải nhanh bài 2.22 trang 42 sgk toán 9 tập 1 kntt

Điều kiện xác định của phương trình  là

A. x          B.              C.           D.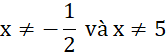 

Giải nhanh:

Đáp án D

Giải nhanh bài 2.23 trang 42 sgk toán 9 tập 1 kntt

Phương trình x – 1 = m + 4 có nghiệm lớn hơn 1 với 

A.                B.                   C.                D. m < -4.

Giải nhanh:

Đáp án C

Giải nhanh bài 2.24 trang 42 sgk toán 9 tập 1 kntt

Nghiệm của bất phương trình 1 – 2x 2 – x là

A.                    B. x <                       C.                 D.

Giải nhanh:

Đáp án C

Giải nhanh bài 2.25 trang 42 sgk toán 9 tập 1 kntt

Cho a > b. Khi đó ta có:

A. 2a > 3b                  b. 2a > 2b + 1           C. 5a + 1 > 5b + 1               D. -3a < -3b – 3.

Giải nhanh:

Đáp án C 

B. TỰ LUẬN

Giải nhanh bài 2.26 trang 42 sgk toán 9 tập 1 kntt

Giải các phương trình sau:

a)                        b) .

Giải nhanh:

a)

(3x – 1 + x + 2)(3x – 1 – x – 2) = 0

(4x + 1)(2x – 3) = 0

Vậy x = .

b) x(x + 1)=.

x(x + 1)=.

x(x + 1)-2(x - 1)(x + 1)=0

x(x + 1)-(2x - 2).(x + 1)

(x + 1)(x – 2x + 2)=0

(x + 1)(-x + 2) =0

Vậy x = -1 và x = 2.

Giải nhanh bài 2.27 trang 42 sgk toán 9 tập 1 kntt

Giải các phương trình sau:

                                  b)

Giải nhanh:

a) ĐKXĐ:

Quy đồng mẫu thức ta được

x(x + 5) – 2(x – 5) = x²

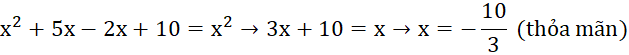
Vậy nghiệm của phương trình là x =

b) ĐKXĐ:

Quy đồng mẫu thức ta đươc

-2x = 2

x = -1

Vậy nghiệm của phương trình là x = -1 (không thỏa mãn)

Vậy phương trình vô nghiệm.

Giải nhanh bài 2.28 trang 42 sgk toán 9 tập 1 kntt

Cho a < b, hãy so sánh:

a) a + b + 5 với 2b + 5;              b) -2a -3 với –(a+b) – 3.

Giải nhanh:

a) a + b + 5 với 2b + 5

Ta có: a < b nên ta có a + b < b + b suy ra a + b + 5 < 2b +5

b) -2a – 3 với –(a + b) - 3

Ta có: a < b nên ta có a + a < b + a suy ra -2a > -(a + b)

Do đó ta có -2a – 3 > - (a + b) - 3.

Giải nhanh bài 2.29 trang 42 sgk toán 9 tập 1 kntt

Giải các bất phương trình:

a) 2x + 3(x + 1) > 5x – (2x – 4);                   b) (x+1)(2x-1) < 2x² - 4x + 1

Giải nhanh:

a) 2x + 3(x + 1) > 5x – (2x – 4)

2x + 3x + 3 > 5x – 2x  + 4

2x > 1

b) (x+1)(2x-1) < 2x² - 4x + 1

5x < 2 =>

Giải nhanh bài 2.30 trang 42 sgk toán 9 tập 1 kntt

Một hãng viễn thông nước ngoài có hai gói cước như sau:

a) Hãy viết một phương trình xác định thời gian gọi (phút) mà phí trả trong cùng một tháng của hai gói cước là hư nhau và giải phương trình đó.

b) Nếu khách hàng chỉ gọi tối đa là 180 phút trong 1 tháng thì nên dùng gói cước nào? Nếu khách hàng gọi 500 phút trong 1 tháng thì ênn dùng gói cước nào?

Giải nhanh:

a) Thời gian gọi trong một tháng là x (phút) (x>0)

Số tiền phải trả khi gọi x phút đối với gói cước B là 44 + 0,25.x(USD)

Số tiền phải trả khi x phút đối với gói cước A là

TH1:

TH2: x > 45 thì phí trả là 32 + 0,4(x - 45)

Vì số tiền phải trả của gói cước B lớn hơn 44 nên để phí trả hai gói cước trong cùng một tháng của hai gói cước là như nhau thì đối với gói cước A thì sẽ rơi vào trường hợp thứ hai nên ta có phương trình:

44 + 0,25.x = 32 + (x - 45).0,4

0,25. x – 0,4x = -44 + 32 – 45.0,4

-0,15 x = -30

x = 200 (thỏa mãn)

Vậy khi gọi 180 phút thì chi phí phải trả đối với hai gói cước là như nhau.

b) Đối với x = 180 số tền phải trả khi dùng gói cước A là: 

32 + (180 – 45).0,4 = 86 (USD)

Đối với x = 180 số tiền phải trả khi dùng gói cước B là:

44 + 0,25.180 = 89 (USD)

Vậy khi gọi tối đa 180 phút trong 1 tháng thì nên dùng gói cước A

Đối với x = 500 số tiền phải trả khi dùng gói cước A là:

32 + (500 – 45).0,4 = 214 (USD)

Đối với x = 500 số tiền phải trả khi dùng gói cước B là:

44 + 0,25.500 = 169 (USD)

Vậy khi gọi 500 phút trong 1 tháng thì nên dùng gói cước B.

Giải nhanh bài 2.31 trang 43 sgk toán 9 tập 1 kntt

Thanh tham dự một kì kiểm ta năng lực tiếng Anh gồm 4 bài kiểm tra nghe, nói, đọc và viết. Mỗi bài kiểm tra có điểm số là nguyên từ 0 đến 10. Điểm trung bình của ba bài kiểm tra nghe, nói, đọc của Thanh là 6,7. Hỏi bài kiểm tra viết của Thanh cần được bao nhiêu điểm để điểm trung bình cả 4 bài kiểm tra từ 7,0 trở lên? Biết điểm trung bình được tính gần đúng đến chữ số thập phân thứ nhất.

Giải nhanh:

Điểm trung bình 3 bài là 6,7 nên tổng điểm 3 bài là:

6,7.3 = 20,1

Điểm trung bình của 4 bài ít nhất là 7,0 nên tổng điểm 4 bài ít nhất là 4.7,0 = 29 

Gọi điểm bài kiểm tra viết của Thanh là x (

Vì tổng điểm 3 bài là 20,1 và bài kiểm tra viết là x điểm nên tổng số điểm là 20,1 + x

Để điểm trung bình của cả 4 bài được từ 7,0 trở lên thì tổng điểm của 4 bài ít nhất là 28 điểm nên ta có bất phương trình  từ đó ta có x

Mà  

Vậy bạn Thanh cần thối thiểu 8 điểm để trung bình cả 4 bài kiểm tra từ 7,0 trở lên.

Giải nhanh bài 2.32 trang 43 sgk toán 9 tập 1 kntt

Để lập đội tuyển năng khiếu về bóng rổ của trường, thầy thể dục đưa ra quy định tuyển chọn như sau: mỗi bạn dự tuyển sẽ ném được 15 quả bóng vào rổ, quả bóng vào rổ được 2 điểm; quả bóng ném ra ngoài bị trừ 1 điểm. Nếu bạn nào có số điểm từ 15 điểm trở lên thì sẽ được chọn vào đội tuyển. Hỏi một học sinh muốn được chọn vào đội tuyển thì ném ít nhất bao nhiêu quả vào rổ?

Giải nhanh:

Gọi số quả bóng ném trúng rổ là x

Số điểm thu được khi ném trúng x quả là 2.x

Tổng số bóng được ném là 15 quả, x quả trúng nên số quả trượt là 15 - x

Số điểm bị mất khi ném trượt 15 - x là (15 - x).1 = 15 - x

Nên số điểm đó thu được khi ném túng được x quả là 2x - (15 - x) = 3x - 15

Số điểm để học sinh được chọn vào đội tuyển thì cần ít nhất là 15 điểm nên ta có bất phương trình