BÀI TẬP CUỐI CHƯƠNG 3

BÀI TẬP TỰ LUẬN

Bài tập 8 trang 89 sgk Toán 8 tập 1 CTST

Cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC sao cho AE = EF = FC. Gọi M là giao điểm của BF và CD, N là giao điểm của DE và AB. Chứng minh rằng:

a) M, N theo thứ tự là trung điểm của CD, AB

b) EMFN là hình bình hành

Giải nhanh:

a) nên (1)

Gọi O là giao điểm hai đường chéo AC và BD của hình bình hành.

Khi đó O là trung điểm của AC và BD. Suy ra (2)

Từ (1) và (2) suy ra Hay

+ Xét BCD có: CO là trung tuyến của tam giác mà  

F là trọng tâm của BCD.

Do đó BM là đường trung tuyến của BCD. M là trung điểm của CD.

+ CMTT đối với ABD ta có E là trọng tâm của tam giác.

Do đó DN là đường trung tuyến của ABD N là trung điểm của AB.

b)  Do M là trung điểm của CD 

       N là trung điểm của AB (câu a) nên

Mà  =>  =>BMDN là hình bình hành. 

+ Ta có E là trọng tâm của ABD nên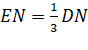

          F là trọng tâm của BCD nên  

Mà DN = BM (cmt)  EN = FM.

+ Xét tứ giác EMFN có: EMFN là hình bình hành.

Bài tập 9 trang 89 sgk Toán 8 tập 1 CTST

Cho tam giác ABC cân tại A. Gọi H, D lần lượt là trung điểm của các cạnh BC và AB.

a) Chứng minh rằng tứ giác ADHC là hình thang.

b) Gọi E là điểm đối xứng với H qua D. Chứng minh rằng tứ giác AHBE là hình chữ nhật.

c) Tia CD cắt AH ở M và cắt BE ở N. Chứng minh tứ giác AMBN là hình bình hành.

Giải nhanh:

a) + Do ABC cân tại A  

Vì AB = AC A nằm trên đường trung trực của BC.

Vì H là trung điểm của BC H nằm trên đường trung trực của BC.

Do đó AH là đường trung trực của BC .

+ Xét AHB vuông tại H:HD là đường trung tuyến =>

+ Tam giác DBH có DB = DH nên là tam giác cân tại D

Suy ra hay

Mà (cmt)

Mà hai góc này ở vị trí đồng vị nên .

+ Xét tứ giác ADHC có: DH // AC ADHC là hình thang.

b) Do E là điểm đối xứng với H qua D D là trung điểm của HE.

Xét tứ giác AHBE có:D là trung điểm của AB;D là trung điểm của HE

Mà AB cắt HE tại D AHBE là hình bình hành.

Mà   (do ) hình bình hành AHBE là hình chữ nhật.

c) + Do AHBE là hình chữ nhật MH // NE Suy ra  

+ Xét MHD và NED có: ; DH = DE;  

Do đó MHD = NED (g.c.g)  DM = DN

Hay D là trung điểm của NM.

+ Xét tứ giác AMBN có: D là trung điểm của AB; NM mà AB cắt NM tại D 

AMBN là hình bình hành.

Bài tập 10 trang 89 sgk Toán 8 tập 1 CTST

Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của AB, AC, BC.

a) Chứng minh tứ giác ANEB là hình thang vuông.

b) Chứng minh tứ giác ANEM là hình chữ nhật.

c) Đường thẳng song song với BN kẻ từ M cắt tia EN tại F. Chứng minh rằng tứ giác AFCE là hình thoi.

d) Gọi D là điểm đối xứng của E qua M. Chứng minh rằng A là trung điểm của DF.

Giải nhanh:

a) + Xét ABC vuông tại A ó: AE là đường trung tuyến

+ Vì EA = EC E nằm trên đường trung trực của AC.

Vì N là trung điểm của AC N nằm trên đường trung trực của AC.

EN là đường trung trực của đoạn thẳng AC

Ta có: BA // EN.

+ Xét tứ giác ANEB có: ANEB là hình thang Mà  

hình thang ANEB là hình thang vuông.

b) Vì EA = EB E nằm trên đường trung trực của AB.

Vì M là trung điểm của AB M nằm trên đường trung trực của AB.

EM là đường trung trực của AB ,  hay

Xét tứ giác ANEM có: ; Mà

ANEM là hình chữ nhật.

c) + Xét tứ giác BMFN có: BMFN là hình bình hành.

Do đó MB = NF.

Mà AM = MB ; AM = EN. Do đó EN = NF hay N là trung điểm của EF.

+ Xét tứ giác AFCE có: N là trung điểm của AC và EF  Mà AC cắt EF tại N AFCE là hình bình hành.

Lại có AFCE là hình thoi.

d) + Do AFCE là hình thoi (câu c) AF // CE và AF = CE.

CMTT câu c, ta cũng có ADBE là hình thoi  

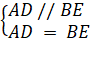
+ Ta có             + Ta có  

Mà CE = BE (do E là trung điểm của BC) AF = AD (2)

Từ (1) và (2) ta có A là trung điểm của DF.

Bài tập 11 trang 89 sgk Toán 8 tập 1 CTST

Cho hình bình hành ABCD có AB = 2AD. Gọi E, F lần lượt là trung điểm của AB và CD. Gọi I là giao điểm của AF và DE, K là giao điểm của BF và CE.

Chứng minh rằng:

a) Tứ giác AECF là hình bình hành.

b) Tứ giác AEFD là hình gì ? Vì sao ?

c) Chứng minh tứ giác EIFK là hình chữ nhật.

d) Tìm điều kiện của hình bình hành ABCD để tứ giác EIFK là hình vuông.

Giải nhanh:

a) + Do ABCD là hình bình hành  

Vì E là trung điểm của AB nên

     F là trung điểm của CD nên

Mà AB = CD (cmt). Do đó .

+ Xét tứ giác AECF có:   AECF là hình bình hành.

b) Xét tứ giác AEFD có: AEFD là hình bình hành.

Mặt khác AB = 2AD 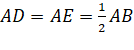=>hình bình hành AEFD là hình thoi.

c) Do AEFD là hình thoi (câu c) nên ta có:

+

+ ED là đường phân giác của góc AEF

CMTT câu c ta cũng có tứ giác BEFC là hình thoi =>

+ EC là đường phân giác của góc BEF

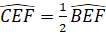
Ta có: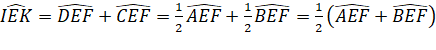 

Mà (hai góc kề bù)

Suy ra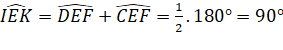

+ Xét tứ giác EIFK có: EIFK là hình chữ nhật.

d) Theo câu c, tứ giác EIFK là hình chữ nhật

Do đó để tứ giác EIFK là hình vuông thì IE = IF   (1)

Xét hình thoi AEFD có:I là trung điểm của AF và DE; AF cắt DE tại I

(2)

Từ (1) và (2) suy ra IA = ID

Xét IAD có: IA = ID IAD cân tại I (DHNB)

Mà (do ) IAD vuông cân tại I Suy ra

Mặt khác AEFD là hình thoi  AF là đường phân giác của góc EAD

Suy ra Hay

Vậy để tứ giác EIFK là hình vuông thì hình bình hành ABCD cần thêm điều kiện hay ABCD là hình chữ nhật.

Bài tập 12 trang 89 sgk Toán 8 tập 1 CTST

Cho hình bình hành ABCD với AD = 2AB. Từ C vẽ CE vuông góc với AB. Nối E với trung điểm M của AD. Từ M vẽ MF vuông góc với CE, MF cắt BC tại N.

a) Tứ giác MNCD là hình gì ?

b) Chứng minh tam giác EMC cân tại M

c) Chứng minh : BADˆ=2AEMˆ

Giải nhanh:

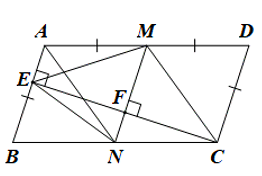
a) + Do ABCD là hình bình hành  

Ta có: ; Mà AB // CD MN // CD.

Xét tứ giác MNCD có: 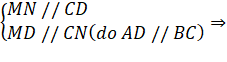MNCD là hình bình hành.

+ Ta có: M là trung điểm của AD hay

Mà AB = MD

Mà AB = CD (do ABCD là hình bình hành)   Do đó MD = CD.

+ Hình bình hành MNCD có MD = CD nên MNCD là hình thoi.

b) + Do MNCD là hình thoi   

Do N là trung điểm của BC.

+ Xét EBC vuông tại E có: EN là đường trung tuyến 

+ Do NE = NC N nằm trên đường trung trực của đoạn thẳng EC

Hay đường trung trực của EC đi qua N và vuông góc với EC.

Lai có NF là đường trung trực của đoạn thẳng BC.

F là trung điểm của EC hay FE = FC.

+ Xét EMF và CMF có: MF chung;  

Do đó EMF = CMF (hai cạnh góc vuông). Suy ra ME = MC

Xét EMC có: ME = MC  EMC cân tại M.

c) + Vì AB // MN (cma) (so le trong)

Ta có EMF = CMF (cmb) 

Do đó

+ Do MNCD là hình thoi MC là đường phân giác của góc DMN

(1)

+ Do DMNC là hình thoi  (hai góc đối bằng nhau)

Do ABCD là hình bình hành (hai góc đối bằng nhau)

Do đó (2)

Từ (1) và (2) ta có  hay