BÀI 1. HAI TAM GIÁC ĐỒNG DẠNG

1. TAM GIÁC ĐỒNG DẠNG

Bài 1:  Nêu nhận xét về hình dạng và kích thước của từng cặp hình: Hình 1a và Hình 1b, Hình 1c và Hình 1d, Hình 1e và Hình 1g

Giải nhanh:

Giống nhau nhưng khác về kích thước.

Bài 2: Cho tam giác ABC và tam giác A'B'C' như Hình 2

a) Hãy viết các cặp góc bằng nhau

b) Tính và so sánh các tỉ số :

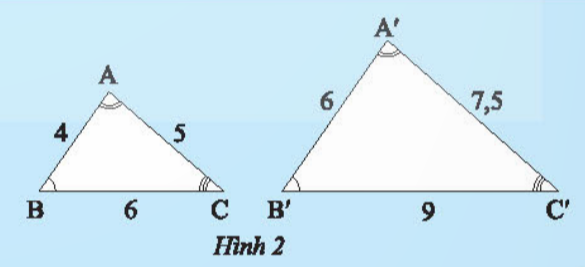
Giải nhanh:

a)

b) ;   ;     =>

Bài 3: Quan sát Hình 3, cho biết ΔAMNᔕΔABC

a) Hãy viết tỉ số của các cạnh tương ứng và tính tỉ số đồng dạng

b) Tính

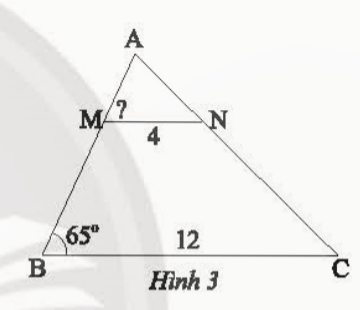
Giải nhanh:

a) ΔAMNᔕΔABC:     b) AMNᔕΔABC: =65⁰

2. TÍNH CHẤT

Bài 1: a) Nếu ΔA′B′C′=ΔABC thì tam giác A'B'C' có đồng dạng với tam giác ABC không? Tỉ số đồng dạng là bao nhiêu?

b) Cho ΔA′B′C′ᔕΔABC theo tỉ số k thì ΔABCᔕΔA′B′C′ theo tỉ số nào?

Giải nhanh:

a) ΔA′B′C′=ΔABC suy ra : ;

Do đó ΔA′B′C′ᔕΔABC theo tỉ số đồng dạng k = 1

b) ΔA′B′C′ᔕΔABC theo tỉ số k nên = k =>

Bài 2: Quan sát Hình 4, cho biết ΔADEᔕΔAMN,ΔAMNᔕΔABC, DE là đường trung bình của tam giác AMN, MN là đường trung bình của tam giác ABC. Tam giác ADE đồng dạng tam giác ABC theo tỉ số đồng dạng là bao nhiêu?

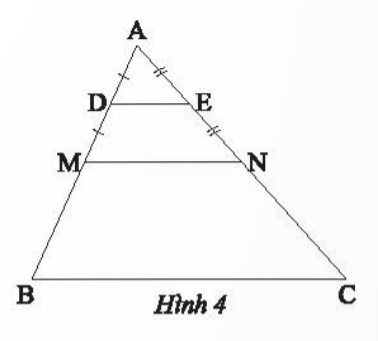
Giải nhanh:

Ta có: ΔADEᔕΔAMN,ΔAMNᔕΔABC suy ra ΔADEᔕΔABC

ΔADEᔕΔAMN theo tỉ số ; ΔAMNᔕΔABC theo tỉ số   

ΔADEᔕΔABC theo tỉ số  

3. ĐỊNH LÍ

Bài 1: Quan sát Hình 5, biết MN // BC. Hãy điền vào ? cho thích hợp

ΔAMN và ΔABC: =?; =?; =?

Nêu nhận xét về mối quan hệ giữa tam giác AMN và tam giác ABC.

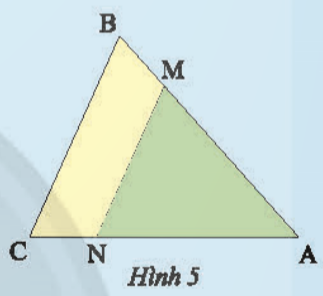
Giải nhanh:

ΔAMN và ΔABC: = ; = ; = => ΔAMNᔕΔABC

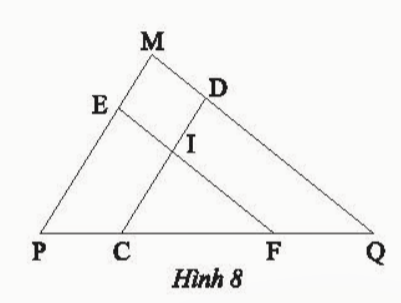
Bài 2: Quan sát Hình 8, cho biết DC // MP, EF // MQ

a) Chứng minh rằng ΔEPFᔕΔDCQ

b) ΔICF có đồng dạng ΔMPQ không? Tại sao?

Giải nhanh:

a) Ta có DC // MP nên ΔDCQᔕΔMPQ; EF // MQ nên ΔEPFᔕΔMPQ

Do đó ΔEPFᔕΔDCQ

b) Ta có IF // DQ nên ΔICFᔕΔDCQ => ΔICFᔕΔMPQ

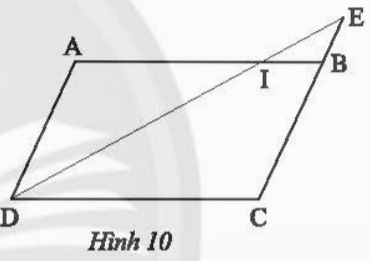
Bài 3: Trong Hình 10, cho biết ABCD là hình bình hành

a) Chứng minh rằng ΔIEBᔕΔIDA

b) Cho biết CB = 3BE và AI = 9 cm. Tính độ dài DC

Giải nhanh:

a) ABCD là hình bình hành suy ra BE // AD =>ΔIEBᔕΔIDA

b) ΔIEBᔕΔIDA suy ra   

Ta có IB // CD nên ΔIEBᔕΔDEC  Do đó nên

Suy ra ⇒IB=3⇒AB=IA+IB=12. Ta có DC = AB = 12 cm

BÀI TẬP CUỐI SGK

Bài 1: Trong khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Tại sao?

a) Hai tam giác bằng nhau thì đồng dạng với nhau

b) Hai tam giác đồng dạng với nhau thì bằng nhau

Giải nhanh:

a) Đúng. Hai tam giác nên chúng đồng dạng theo tỉ số 1

b) Sai. Hai tam giác đó bằng nhau khi và chỉ khi k = 1

Bài 2: Cho tam giác ABC, hãy vẽ một tam giác đồng dạng với tam giác ABC theo tỉ số đồng dạng k=

Giải nhanh:

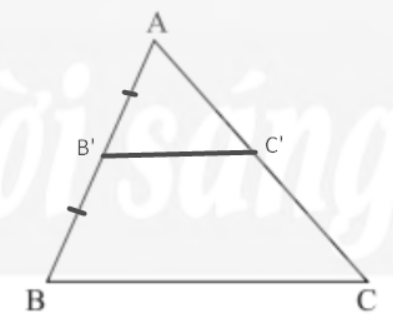
lấy B' là trung điểm của AB; Qua B' kẻ đường song song với BC cắt AC tại C'

Ta có: B'C' // BC nên ΔAB′C′ᔕΔABC theo tỉ số đồng dạng k=

Bài 3:

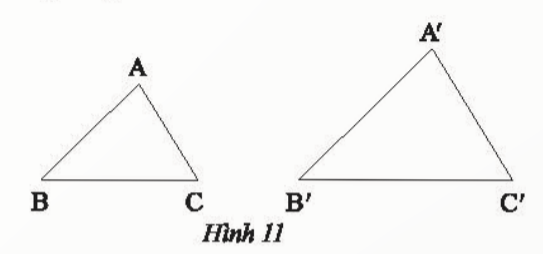
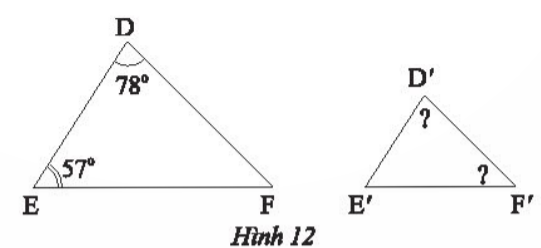
a) Trong Hình 11, cho biết ΔABCᔕΔA′B′C′. Viết tỉ số đồng dạng của các cạnh tương ứng và chỉ ra các cặp góc tương ứng.

b) Trong Hình 12, cho biết ΔDEFᔕΔD′E′F′. Tính số đo  và

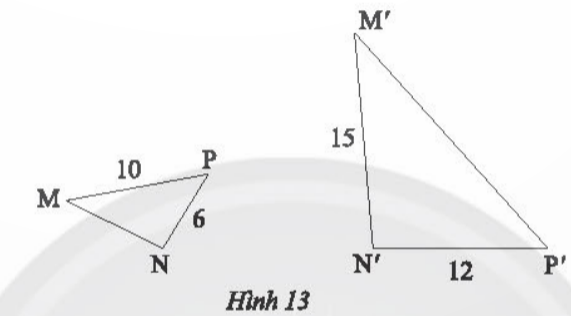
c) Trong Hình 13, cho biết ΔMNPᔕΔM′N′P′. Tính độ dài các đoạn thẳng MN và M'P'

Giải nhanh:

a) ΔABCᔕΔA′B′C′ nên ta có: = ; = ; = ; =

b) ΔDEFᔕΔD′E′F′ nên ta có: = = 78⁰= = 180⁰ –( 78⁰+ 57⁰) = 45⁰

c) ΔMNPᔕΔM′N′P′ nên ta có : = = Suy ra MN= , M′P′=20

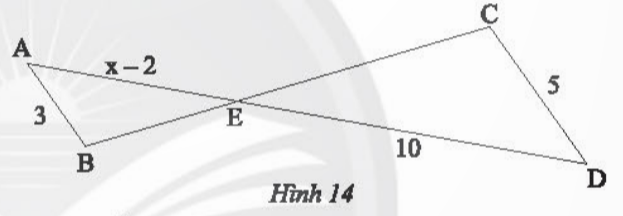
Bài 4: Trong Hình 14, cho biết AB // CD.

a) Chứng minh rằng ΔAEBᔕΔDEC   b) Tìm x

Giải nhanh:

a) Ta có AB // CD nên = = ; lại có = Suy ra ΔAEBᔕΔDEC

b) ΔAEBᔕΔDEC nên => => x = 8

Bài 5: Cho ΔABCᔕΔDEF theo tỉ số đồng dạng k=

a) Tính tỉ số chu vi của hai tam giác đã cho

b) Cho biết hiệu chu vi của hai tam giác trên là 36 cm, tính chu vi của mỗi tam giác

Giải nhanh:

a) ΔABCᔕΔDEF nên = =

Chu vi tam giác ABC: P_ABC=AB+BC+AC= (DE+EF+DF)       

Chu vi tam giác DEF: P_DEF=DE+EF+DF =>Tỉ số chu vi của hai tam giác

b) Ta có: P_DEF − P_ABC = 36 => P_DEF - P_DEF  = 36 => P_DEF = 60 =>  P_ABC = 24 (cm)

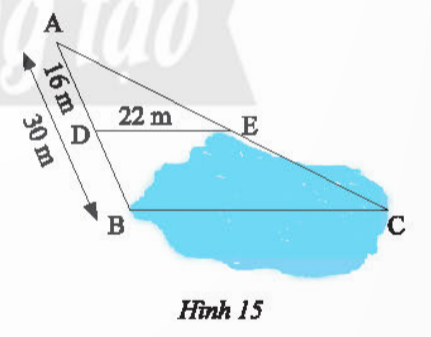
Bài 6: Người ta ứng dụng hai tam giác đồng dạng để đo khoảng cách BC ở hai địa điểm không thể đến được (Hình 15). Biết DE // BC

a) Chứng minh rằng ΔADEᔕΔABC            b) Tính khoảng cách BC

Giải nhanh:

a) Tam giác ABC: DE // BC nên ΔADEᔕΔABC

b) ΔADEᔕΔABC nên => => BC = (m)