Bài 1 trang 59 SBT Toán 8 tập 2 CTST: Cho tam giác ABC, hãy vẽ tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số đồng dạng $k=\frac{3}{5}$

Giải

Trên cạnh AB lấy điểm D sao cho AD = $\frac{3}{5}$AB.

Từ D kẻ đường thẳng song song với BC và cắt AC tại E.

Ta có $\Delta ADE$ có $\Delta {ABC}$ theo tỉ số đồng dạng k =$\frac{AD}{AB} =\frac{3}{5}$

Dựng $\Delta A'B'C' = \Delta ADE$.

Dựng A'B' =AD.

Dựng cung tròn tâm A bán kính AE và cung tròn tâm B bán kính DE, hai cung cắt nhau tại C’.

Nối B'C', A'C' ta được tam giác A'B'C' phải dựng.

Ta có $\Delta ADE \sim  \Delta ABC$ theo tỉ số k =$\frac{3}{5}$ nên  $\Delta A'B'C'$ ở $ \Delta ABC$ theo tỉ số k =$\frac{3}{5}$

Bài 2 trang 59 SBT Toán 8 tập 2 CTST: Trong Hình 5, cho biết MN là đường trung bình của tam giác ABC. Tam giác ADE đồng dạng với tam giác ABC theo tỉ số $k=\frac{2}{3}$

a) Chứng minh rằng $\Delta ADE  \sim  \Delta AMN$

b) Tính tỉ số đồng dạng của $\Delta  ADE$ và $\Delta AMN$

Giải

a)$\Delta ADE \sim  \Delta ABC$ (giả thiết).

Ta có MN // BC (MN là đường trung bình của ) $\Delta ABC$). 

Suy ra $\Delta ABC \sim \Delta AMN.$

Do đó $\Delta ADE \sim \Delta AMN$.

b)Ta có  $\Delta ADE \sim  \Delta ABC$ theo tỉ số $\frac{AD}{AB} =\frac{2}{3}$ 

$\Delta ABC \sim  \Delta AMN$ theo tỉ số $ \frac{AB}{AM} =2$ 

$\Rightarrow \frac{AD}{AB} . \frac{AB}{AM} = \frac{2}{3} . 2 $ hay $\frac{AD}{AM} =\frac{4}{3}$

Vậy  $\Delta ADE \sim  \Delta AMN$ theo tỉ số $ \frac{AD}{AM} =\frac{4}{3}$ 

Bài 3 trang 59 SBT Toán 8 tập 2 CTST: Trong Hình 6, cho biết $\Delta ABC \sim \Delta DEF$.

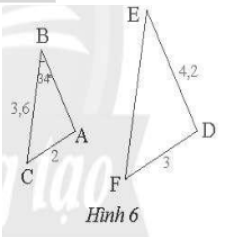
a) Tính số đo $\widehat{E}$.

b) Tính độ dài các đoạn thẳng AB và EF.

Giải

a) Ta có $\Delta ABC \sim \Delta DEF$ (giả thiết)

nên $\widehat{E} =\widehat{B} = 34^{\circ}$.

b) $\Delta ABC \sim \Delta DEF$ suy ra 

$\frac{AB}{DE} = \frac{BC}{EF}= \frac{AC}{DF}$ hay $\frac{AB}{4,2}=\frac{3,6}{EF}= \frac{2}{3}$

Vậy AB = 2,8;  EF= 5,4.

Bài 4 trang 59 SBT Toán 8 tập 2 CTST: Trong Hình 7, cho biết RV là tia phân giác của $\widehat{SRT}$ và UV // RT. Chứng minh rằng:

a)$\Delta SUV \sim \Delta SRT$

b) $\frac{SU}{UR} = \frac{SR}{RT}$

Giải

a) Ta có UV // RT (giả thiết), suy ra )$\Delta SUV \sim \Delta SRT$

b) Ta có $\widehat{RVU} = \widehat{VRT}$ (hai góc so le trong),

$\widehat{URV} = \widehat{VRT}$ (RV là tia phân giác của $\widehat{SRT}$).

Suy ra $\widehat{RVU}= \widehat{URV}$ nên $\Delta{RUV}$ cần lại U. Do đó UR = UV

Мà $\frac{SU}{ SR} = \frac{UV}{ RT} (\Delta SUV \sim \Delta SRT$). 

Vậy $\frac{UR}{ RT}$

Bài 5 trang 59 SBT Toán 8 tập 2 CTST: Trong Hình 8, cho biết tứ giác ABCD là hình bình hành. Tìm x.

Giải

Ta có AE // DC (ABCD là hình bình hành).

Suy ra $\Delta IAE \sim  \Delta IDC$

Suy ra $\frac{IE}{IC} = \frac{AE}{DC} $ hay $\frac{2,8}{x-3}= \frac{3,2}{6,4}$ 

Do đó x − 3 – 5,6. Vậy x=8,6.

Bài 6 trang 60 SBT Toán 8 tập 2 CTST: Trong Hình 9, cho biết $\Delta {ABC} \sim \Delta DEF, \Delta DEF \sim \Delta IHK$. Tính độ dài các đoạn thẳng AB, EF, IH và HK

Giải

Ta có $\Delta ABC \sim \Delta DEF$ 

Suy ra $\frac{AB}{DE} =\frac{BC}{EF} = \frac{AC}{DF} hay $\frac{AB}{4,2} = \frac{3,6}{EF}=\frac{2}{3}$ 

Suy ra AB = 2,8; EF = 5,4

Ta có $\Delta DEF \sim \Delta IHK$ 

Suy ra $\frac{DE}{IH} = \frac{EF}{HK}= \frac{DF}{IK} $ hay $\frac{4,2}{IH} =\frac{5,4}{HK}=\frac{3}{4,5}

Suy ra IH = 6,3; HK = 8,1

Bài 7 trang 60 SBT Toán 8 tập 2 CTST: Người ta ứng dụng hai tam giác đồng dạng để đo khoảng cách BC ở hai điểm không đến được (Hình 10). Biết AD // BC.

a) Chứng minh rằng $\Delta IDA \sim \Delta ABC$.

b) Tính khoảng cách BC.

Giải

a) Ta có AD // BC (giả thiết), suy ra $\Delta{IDA} \sim  \Delta {ABC}$.

b) Ta có  $\Delta{IDA} \sim \Delta{IBC}$ (chứng minh trên).

Suy ra $\frac{IA}{ IC} = \frac{AD}{BC}$ hay $\frac{  12}{36} =\frac{ 17}{BC}$

Vậy BC = 51 (m).