Bài 1 trang 41 SBT Toán 8 tập 2 CTST: Trên một đường thẳng, đặt ba đoạn thẳng liên tiếp AB =BC=CD. Tìm tỉ số $\frac{AB}{BD};\frac{AB}{AD};\frac{AC}{AD}$.

Giải

Ta có 

$\frac{AB}{BD} = \frac {AB}{BC+CD} = \frac {AB}{AB+ AB} =\frac{1}{2}$

$\frac{AB}{AD}=\frac{AB}{AB+ BC+ CD }= \frac{AB}{AB+ AB+AB} = \frac{1}{3}$

$\frac{AC}{AD}= \frac{AB+ BC}{AB+ BC+ CD }= \frac{AB+ AB}{AB+ AB+ AB } = \frac{2}{3}$

Bài 2 trang 42 SBT Toán 8 tập 2 CTST: Cho đoạn thẳng AB có độ dài bằng 10 cm. Lấy điểm C thuộc đoạn thẳng AB sao cho $\frac{CA}{CB}= \frac{3}{2}$. Lấy D thuộc tia đối của tia BA sao cho $\frac{DA}{DB}= \frac{3}{2}$. Tính độ dài:

a) CB;

b) DB;

c) CD.

Giải

a) Ta có $\frac{CA}{CB}= \frac{3}{2}$

$\left\{\begin{matrix} CA =&  3t \\ CB =& 2t  \\ \end{matrix}\right.$ với t > 0 

Nên AB = 10 cm = CA + CB = 5t ⇔ t = 2

Vậy CB = 4 cm

b) Ta có $\frac{DA}{DB}= \frac{3}{2}$ 

$\left\{\begin{matrix} DA =&  3t \\ DB =& 2t  \\ \end{matrix}\right.$ với t > 0 

Mặt khác D thuộc tia đối của tia BA nên DA > DB

Do đó AB = 10 cm = DA - DB = 3t - 2t ⇔ t = 10 cm

Vậy DB = 20 cm

c) Ta có CD= CB + DB = 24 cm 

Bài 3 trang 42 SBT Toán 8 tập 2 CTST: Trong Hình 10, cho biết QR // NP và MQ = 10 em, QN= 5 cm, RP= 6 cm. Tính độ dài MR.

Giải

Theo thales : $\frac{MQ}{NQ} =\frac{MR}{RP}$

$ \Rightarrow \frac{10}{5} = \frac{MR}{6} \Rightarrow MR = 12 cm$

Bài 4 trang 42 SBT Toán 8 tập 2 CTST: Tính các độ dài x, y trong Hình 11.

Giải

a)Theo thales: $\frac{AM}{BM} = \frac{AN}{CN}$

Ta lại biết CN = AC - AN = 4 cm

$\Rightarrow x = \frac{12}{5} $ cm 

b) Ta có  $\left\{\begin{matrix} MN \perp  AB\\ AC \perp  AB  \\ \end{matrix}\right. $

$\Rightarrow $MN // AC}

Theo thales: $\frac{BM}{BA} = \frac{BN}{BC}$

$\Rightarrow y = \frac{21}{5} $ cm 

Bài 5 trang 42 SBT Toán 8 tập 2 CTST: Cho tam giác ABC có AM là đường trung tuyến ($M \in BC$). Lấy điểm E thuộc AM sao cho AE = 3EM. Tia BE cắt AC tại N. Tính tỉ số $\frac{AN}{NC}$

Giải

Vẽ EN // MP ( P thuộc AC)

$\Delta AMP$ có $EN // MP \Rightarrow \frac{AN}{NP} = \frac{AE}{EM} = 3$ (1)

 $\Delta CNB$ có $EN // MP \Rightarrow \frac{NP}{NC} = \frac{MB}{BC} = \frac{1}{2}$ (2)

Từ (1) và (2) $\Rightarrow \frac{AN}{NP} . \frac{NP}{NC} = 3. \frac{1}{2} \Rightarrow \frac{AN}{NC} = \frac{3}{2}$

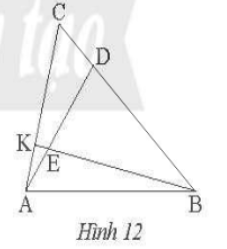
Bài 6 trang 42 SBT Toán 8 tập 2 CTST: Cho tam giác ABC và điểm D trên cạnh BC sao cho

$\frac{BD}{BC} =\frac{ 3}{4}$, điểm E trên đoạn AD sao cho $\frac{AE}{AD} =\frac{1}{3}$. Gọi K là giao điểm của BE và AC. Tính tỉ số $\frac{AK}{KC}$

Giải

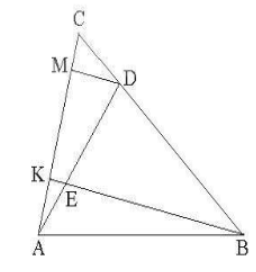
Vẽ DM // BK ($M \in AC$). Ta có:

$\frac{AK}{KM} = \frac{AE}{ED} =\frac{1}{2}$, suy ra $AK = \frac{1}{2} KM$;

$\frac{KM}{KC} = \frac{BD}{BC} =\frac{3}{4}$ , suy ra $KM = \frac{3}{4} KC$;

Suy ra $AK= \frac{3}{8} KC$, suy ra $\frac{AK}{KC} = \frac{3}{8} $;

Bài 7 trang 42 SBT Toán 8 tập 2 CTST: Cho tam giác ABC và điểm M trên cạnh AB sao cho $\frac{AM}{MB} = \frac{3}{2}$ Kẻ MN // BC ($N \in AC$). Cho biết BC=6 cm, tính độ dài MN.

Giải

Ta có MN // AC 

Theo thales 

$\frac{MN}{BC} = \frac{AM}{AB} =\frac{3}{5}$, suy ra $MN=\frac{3}{5}BC =

frac{18}18{5}$ cm 

Bài 8 trang 42 SBT Toán 8 tập 2 CTST: Cho tam giác ABC vuông tại A và MN // BC ($M \in AB; N \in AC$). Biết AB = 9 cm, AM=3 cm, AN =4 cm. Tính độ dài NC, MN, BC. 

Giải

Vì MN// BC 

Theo thales ta có 

$\frac{AM}{AB} = \frac{AN}{AC} = \frac{MN}{BC}$

$\Rightarrow AC = \frac{AN.AB}{AM} = 12$ cm

NC = AC - AN = 12 -4 =8cm 

Xét $\Delta ABC$ vuông tại A