Giải SBT Toán 8 tập 2 Chân trời bài 1 Mô tả xác suất bằng tỉ số
Giải chi tiết sách bài tập Toán 8 tập 2 Chân trời sáng tạo bài 1 Mô tả xác suất bằng tỉ số. Tech12h sẽ hướng dẫn giải tất cả câu hỏi và bài tập với cách giải nhanh và dễ hiểu nhất. Hi vọng, thông qua đó học sinh được củng cố kiến thức và nắm bài học tốt hơn.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Bài 1 trang 87 SBT Toán 8 tập 2 CTST: Một hộp đựng 20 tấm thẻ cùng loại được đánh số thứ tự 1; 2; …; 20. Lấy ngẫu nhiên một thẻ từ hộp. Hãy nêu các kết quả thuận lợi cho mỗi biến cố sau:
A: “Số ghi trên thẻ lấy ra là bội của 5”;
B: “Số ghi trên thẻ lấy ra là ước của 24”.
Giải
Các kết quả thuận lợi của biến cố A là: 5; 10; 15; 20.
Các kết quả thuận lợi của biến cố B là: 1; 2; 3; 4; 6; 8; 12.
Bài 2 trang 87 SBT Toán 8 tập 2 CTST: Cho tấm bìa hình tròn như Hình 2. Xoay tấm bìa quanh tâm của nó và xem khi tấm bìa dừng lại, mũi tên chỉ vào ô ghi số nào.
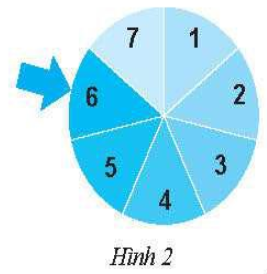
Hãy nêu các kết quả thuận lợi cho mỗi biến cố sau:
A: “Mũi tên chỉ vào ô ghi số lớn hơn 3”;
B: “Mũi tên chỉ vào ô ghi số lẻ”.
Giải
Các kết quả thuận lợi của biến cố A là: ô ghi số 4; ô ghi số 5; ô ghi số 6; ô ghi số 7.
Các kết quả thuận lợi của biến cố B là: ô ghi số 1; ô ghi số 3; ô ghi số 5; ô ghi số 7.
Bài 3 trang 88 SBT Toán 8 tập 2 CTST: Một hộp kín chứa 4 viên bi màu xanh, 6 viên bi màu đỏ có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp. Tính xác suất của các biến cố sau:
A: “Viên bi lấy ra có màu xanh”;
B: “Viên bi lấy ra có màu đỏ”;
C: “Viên bi lấy ra có màu vàng”.
Giải
Vì hộp kín chứa 4 viên bi màu xanh, 6 viên bi màu đỏ có cùng kích thước và khối lượng nên có 10 kết quả có cùng khả năng xảy ra đối với phép thử lấy ra ngẫu nhiên 1 viên bi từ hộp.
Số các kết quả thuận lợi của biến cố A là 4. Xác suất của biến cố A là: $P(A) = \frac{4}{10} = \frac{2}{5}$
Số các kết quả thuận lợi của biến cố B là 6. Xác suất của biến cố B là: $P(B) = \frac{6}{10} = \frac{3}{5}$
Số các kết quả thuận lợi của biến cố C là 0. Xác suất của biến cố C là: $P(C) = $
Bài 4 trang 88 SBT Toán 8 tập 2 CTST: Mật khẩu mở điện thoại của bác Minh là một dãy số gồm 6 chữ số. Vì bác Minh quên mất chữ số cuối cùng của mật khẩu nên bác chọn ngẫu nhiên một 1 chữ số để thử vào vị trí đó. Tính xác suất để bác Minh mở được điện thoại.
Giải
Vì bác Minh quên mất chữ số cuối cùng của mật khẩu nên có 10 kết quả đồng khả năng bác Minh cho phép thử chọn ngẫu nhiên một 1 chữ số để vào vị trí bị quên.
Xác suất để bác Minh mở được điện thoại là: $P = \frac{1}{10}$
Bài 5 trang 88 SBT Toán 8 tập 2 CTST: Một nhóm học sinh gồm 2 bạn quê ở Hà Giang, 4 bạn quê ở Đà Nẵng, 4 bạn quê ở Cần Thơ và 6 bạn quê ở Hà Nội. Chọn ngẫu nhiên 1 bạn trong nhóm. Tính xác suất của các biến cố sau:
A: “Bạn được chọn quê ở Cần Thơ”;
B: “Bạn được chọn quê ở miền Bắc”.
Giải
Vì một nhóm học sinh gồm 2 bạn quê ở Hà Giang, 4 bạn quê ở Đà Nẵng, 4 bạn quê ở Cần Thơ và 6 bạn quê ở Hà Nội nên có 16 kết quả có cùng khả năng xảy ra đối với phép thử chọn ngẫu nhiên 1 bạn trong nhóm.
Số kết quả thuận lợi của biến cố A là 4 nên xác suất của biến cố A là: $P(A) = \frac{4}{16} = \frac{1}{4}$
Số kết quả thuận lợi của biến cố B là 8 nên xác suất của biến cố B là: $P(B) = \frac{8}{16} = \frac{1}{2}$
Bài 6 trang 88 SBT Toán 8 tập 2 CTST: Một hộp chứa 20 quả bóng màu xanh và một số quả bóng màu đỏ. Các quả bóng có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 quả bóng từ hộp. Biết rằng xác suất của biến cố “Quả bóng lấy ra có màu xanh” là 0,4. Hỏi trong hộp có bao nhiêu quả bóng màu đỏ?
Giải
Gọi số quả bóng màu đỏ là x (quả).
Vì hộp chứa 20 quả bóng màu xanh và một số quả bóng màu đỏ và các quả bóng có cùng kích thước và khối lượng nên số có 20 + x kết quả có cùng khả năng xảy ra đối với phép thử lấy ra ngẫu nhiên 1 quả bóng từ hộp.
Số kết quả thuận lợi của biến cố “Quả bóng lấy ra có màu xanh” là: 20.
Vì xác suất của biến cố “Quả bóng lấy ra có màu xanh” là 0,4 nên ta có:
$\frac{20}{20+x} = 0,4$
20 + x = 50
x = 30
Vậy trong hộp có 30 quả bóng màu đỏ.
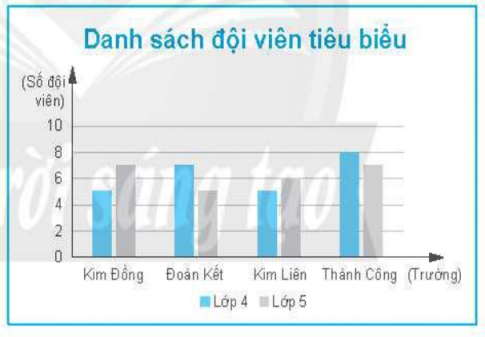
Biểu đồ bên thống kê số đội viên tiêu biểu của các trường tiểu học trên một thị trấn tham dự một buổi giao lưu. Chọn ngẫu nhiên 1 đội viên trong buổi giao lưu đó. Tính xác suất của các biến cố sau:
A: “Đội viên được chọn học lớp 5 trường Tiểu học Kim Đồng";
B: “Đội viên được chọn học trường Tiểu học Đoàn Kết”;
C: “Đội viên được chọn học lớp 4”.
Giải
Tổng số đội viên tham gia buổi giao lưu là: 5+7+7+5+5+6+8+7=50
Do đó, có 50 kết quả có cùng khả năng xảy ra đối với phép thử chọn ngẫu nhiên 1 đội viên trong buổi giao lưu đó.
Số các kết quả thuận lợi của biến cố A là 7. Xác suất của biến cố A là: $P(A) = \frac{7}{50}$
Số các kết quả thuận lợi của biến cố B là 12. Xác suất của biến cố B là:$P(B) = \frac{12}{50}= \frac{6}{25}$
Số các kết quả thuận lợi của biến cố C là 25. Xác suất của biến cố C là:$P(C) = \frac{25}{50}= \frac{1}{2}$
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây

Bình luận