Bài 1 trang 48 SBT Toán 8 tập 2 CTST: Cho tam giác ABC vuông tại A. Tia phân giác của $\widehat{BAC}$ cắt BC tại D. Cho biết DB=15 cm, DC = 20 cm. Tính độ dài AB, AC.

Giải

Sử dụng tính chất đường phân giác

$\frac{AB}{AC} = \frac{BD}{DC} = \frac{15}{20} = \frac{3}{4} $ (1)

Áp dụng định lý Pitago cho tam giác vuông ABC: 

$AB^{2} + AC^{2} = BC^{2} = (BD+ DC)^{2} = 35^{2} = 1225$ (2) 

Từ (1) và (2) 

$\Rightarrow \frac{AB}{3} = \frac{AC}{4} \Rightarrow \frac{AB^{2}}{9} = \frac{AC^{2}}{16} = \frac{AB^{2} + AC^{2}}{9+16} =\frac{1225}{25} = 49$

$\Rightarrow AB^{2} = 441 , AC^{2} = 784$ 

Vậy AB  21 cm; AC = 28cm

Bài 2 trang 48 SBT Toán 8 tập 2 CTST: Cho $\Delta {ABC}$ có AB=6cm,AC=9 cm,BC=10 cm. Tia phân giác của$\widehat{BAC}$ cắt BC tại D, tia phân giác của góc ngoài tại đỉnh A cắt BC tại E. Tính độ dài DB, DC, EB.

Giải

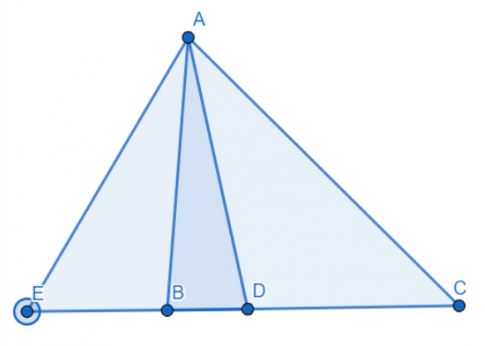
Xét $\Delta ABC$ có AD là đường phân giác áp dụng tính chất đường phân giác

$\Rightarrow \frac{AB}{AC} = \frac{DB}{DC} = \frac{6}{9}=\frac{2}{3}$

$ \Rightarrow \frac{DB}{2} = \frac{DC}{3} =\frac{DB + DC}{5} = \frac{BC}{5} =\frac{10}{5} =2 $

$\Rightarrow DB = 4cm ; DC = 6cm$

Xét $\Delta ABC$ có AE là đường phân giác ngoài tại đỉnh A áp dụng tính chất đường phân giác

$\Rightarrow \frac{EB}{EC} = \frac{AB}{AC}=\frac{6}{9} =\frac{2}{3}$

$ \Rightarrow \frac{EB}{2} = \frac{EC}{3} =\frac{EC - EB}{1} = \frac{BC}{1} =\frac{10}{1} =10 $

$\Rightarrow EB = 20cm$

Bài 3 trang 48 SBT Toán 8 tập 2 CTST: Cho tam giác ABC có các đường phân giác AD, BE, CF ($D \in BC, E \in AC, F \in AB$) cắt nhau tại I.

Chứng minh:

a)$\frac{DI}{DA} = \frac{BC}{AB+BC+CA}$;

b)$\frac{DI}{DA} + \frac{EI}{EB} + \frac{FI}{FC} = 1$

Giải

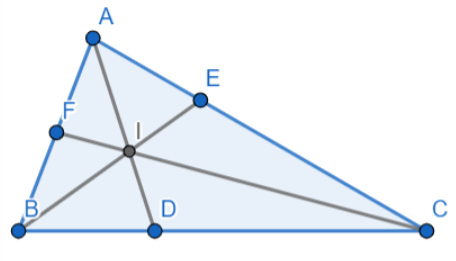
a)Áp dụng tính chất đường phân giác trong tam giác ta có

$\frac{IA}{ID} = \frac{AB}{BD} \Rightarrow \frac{IA}{AB} =\frac{ID}{BD} = \frac{IA+ ID}{AB+ BD} = \frac{AD}{AB+BD}$

$\Rightarrow \frac{AD}{ID} = \frac{AB+BD}{BD} $ (1)

Tương tự $\frac{IA}{ID} = \frac{CA}{CD} \Rightarrow \frac{IA}{CA} =\frac{ID}{CD} = \frac{IA+ ID}{CA+ CD} = \frac{AD}{CA+CD}$

$\Rightarrow \frac{AD}{ID} = \frac{CA+CD}{CD} $ (2)

Từ (1) và (2) suy ra:

$\frac{AD}{ID} = \frac{AB+ BD}{BD}=\frac{CA+CD}{CD} = \frac{AB+BD+CA+CD}{BD+CD}=\frac{AB+ BC+CA}{BC} $

Suy ra $\frac{DI}{DA} = \frac{BC}{AB+ BC+CA}$

b) Sử dụng kết quả phần a) $\frac{DI}{DA} = \frac{BC}{AB+ BC+CA}$

Bằng cách chứng minh hoàn toàn tương tự ta cũng có:

$\frac{EI}{EB} = \frac{CA}{AB+BC+CA} ; \frac{FI}{FC} = \frac{AB}{AB+BC+CA}$

Suy ra  $\frac{DI}{DA} + \frac{EI}{EB} + \frac{FI}{FC} = 1$ (dpcm)

Bài 4 trang 48 SBT Toán 8 tập 2 CTST: Cho hình bình hành ABCD có tia phân giác của góc A cắt đường chéo BD tại M và tia phân giác của góc D cắt đường chéo AC tại N. Chứng minh MN // AD.

Giải

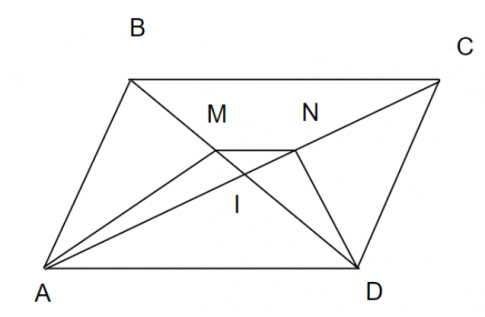
Gọi I là giao điểm của BD và AC

Xét $\Delta ABD$ có tia phân giác AM 

$\frac {AB}{AD} = \frac{BM}{DM}$

Tương tự ta có: $\frac{CD}{AD} = \frac{CN}{AN}$

Mà AB = CD $\Rightarrow \frac{BM}{DM} = \frac{CN}{AN}$

$\Rightarrow \frac{BM}{DM} + 1 = \frac{CN}{AN} +1  \Leftrightarrow \frac{BD}{DM} = \frac{AC}{AN}  \Leftrightarrow \frac{AI}{DM} = \frac{AI}{AN}$

$\Rightarrow MN // AD$ (dpcm)

Bài 5 trang 48 SBT Toán 8 tập 2 CTST: Cho tam giác ABC cân ở A. Tia phân giác của ABC cắt AC tại D. Cho biết BC=10 cm, AB=15 cm. Tính DA, DC.

Giải

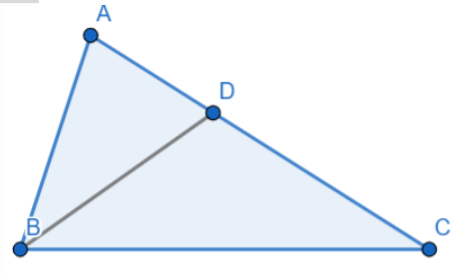
Vì BD là đường phân giác của $\Delta ABC$

$\frac{DA}{DC} = \frac{BA}{BC} = \frac{15}{10} =\frac{3}{2}$

Vì $\Delta ABC$ cân tại A nên AC = AB = 15 cm 

$\frac{DA}{3} = \frac{DC}{2} = \frac{DA+ DC}{5} = \frac{15}{5} = 3$

Suy ra DA = 9 cm; DC = 6 cm

Bài 6 trang 48 SBT Toán 8 tập 2 CTST: Cho tam giác ABC có đường trung tuyến AM (M = BC). Tia phân giác của $\widehat{AMB}$ cắt AB tại D, tia phân giác của $\widehat{AMC}$ cắt AC tại E.

a) Chứng minh DE // BC.

b) Gọi I là giao điểm của DE với AM. Chứng minh I là trung điểm của DE.

Giải

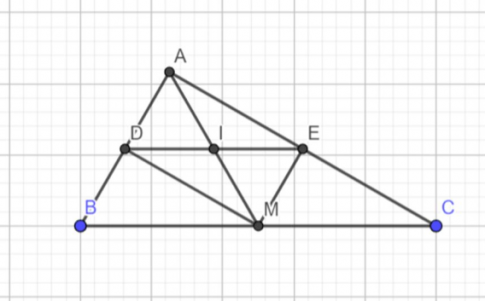
a)Ta có M là trung điểm $BC  \Rightarrow MB = MC$

Mà MD,ME là phân giác $\widehat{AMB}, \widehat{AMC}$

$\Rightarrow \frac{DA}{DB} = \frac{MA}{MB} = \frac{MA}{MC} = \frac{EA}{EC} $

$\Rightarrow DE // BC$

b) Ta có điều cm ở câu a) DE // BC 

$\Rightarrow \frac{ID}{MB} = \frac{AI}{AM} = \frac{IE}{MC} $ 

ta lại có MB = MC suy ra ID = IE như vậy I là trung điểm của DE