A.CÂU HỎI TRẮC NGHIỆM

Câu 1 trang 18 SBT Toán 8 tập 2 CTST: Trong các hàm số sau, hàm số nào là hàm số bậc nhất?

A.$y= 1 - \frac{1}{x}$

B.$y= 2\frac{2x}{3}$

C.$y= x^{2} + 1$

D.$y= 2\sqrt{x}  + 1$

Giải

Đáp án đúng B.$y= 2\frac{2x}{3}$

Câu 2 trang 18 SBT Toán 8 tập 2 CTST: Trong các điểm sau, điểm nào thuộc đồ thị hàm số y=2–4x?

A. (1:1).

B. (2:0).

C. (1;-1).

D. (1;-2).

Giải

Đáp án đúng D. (1;-2).

Thay tọa độ (1; -2) vào phương trình y=2–4x phương trình đúng

Câu 3 trang 18 SBT Toán 8 tập 2 CTST: Nếu hai đường thẳng d y=-3x+4 và d:y=(m+2)x+m song song với nhau thì m bằng

A. 2.

B.3.

C.-5.

D.-3.

Giải 

Đáp án đúng C.-5

Hai đường thẳng song song với nhau có a bằng nhau, Thay a = -3 vào ta được -3 = m + 2 suy ra  m = -5

Câu 4 trang 18 SBT Toán 8 tập 2 CTST: Đường thẳng song song với đường thẳng y = 5x và cắt trục tung lại điểm có tung độ bằng 1 là:

A. y=5x-1. 

B. y=-5x-1. 

C. y=5x+1.

D. y=4-5(1-x).

Giải

Đáp án đúng C. y=5x+1.

Vì 2 đường thẳng song song ta có hệ số a = 5 và điểm cắt trục tung là (0, 1).

Câu 5 trang 18 SBT Toán 8 tập 2 CTST: Cho hai đường thẳng $y=\frac{1}{4} x+4$ và $y=\frac{1}{4}x−4$. Hai đường thẳng đã cho

A. Cắt nhau tại điểm có hoành độ là 4.

B. Song song với nhau

C. Cắt nhau tại điểm có tung độ là 4.

D. Trùng nhau

Giải

Đáp án đúng B. Song song với nhau

Câu 6 trang 18 SBT Toán 8 tập 2 CTST: Cho hàm số $y =\frac{-x + 9}{9}$. Phát biểu nào sau đây đúng về đồ thị của hàm số đã cho?

A. Là một đường thẳng có hệ số b là 9

B. Không phải là một đường thẳng

C. Cắt Trục hoành tại điểm có hoành độ là 9.

D. Đi qua điểm (19;1)

Giải

Đáp án đúng C. Cắt Trục hoành tại điểm có hoành độ là 9.

Đặt y = 0 ta có 

$0 = \frac{-x+9}{9}  \Rightarrow x =9 $

Câu 7 trang 18 SBT Toán 8 tập 2 CTST: Đồ thị của hàm số $y=-\frac{x}{4} + 4$ có dạng giống với đồ thị nào dưới đây

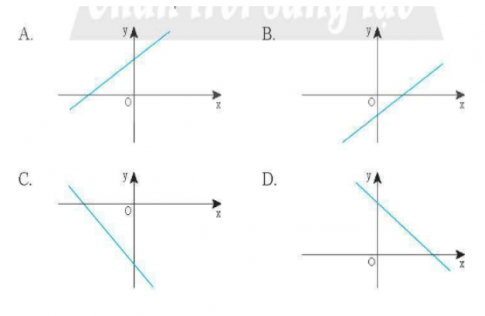
Giải

Đáp án đúng D

Câu 8 trang 19 SBT Toán 8 tập 2 CTST: Đoạn thẳng trong hình vẽ bên là tập hợp những điểm (x; y) thoả mãn điều kiện nào dưới đây?

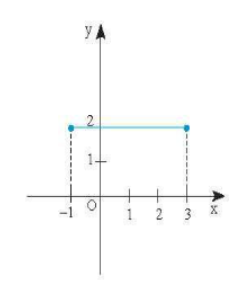
A-1<y<3 và x=2.

B.1≤x≤3 và y≤2.

C.−1≤x≤3 và y=2.

D. x>−1 và y=2.

Giải

Đáp án đúng C.−1 ≤ x ≤3 và y=2.

Câu 9 trang 19 SBT Toán 8 tập 2 CTST: Cho hàm số y=5x+ 10. Giá trị của hàm số tại x=a−1 là

A. 5a+5.

B. 5a + 15.

C. 5a+3.

D. 5a - 5. 

Giải

Đáp án đúng A. 5a+5.

Thay x =a -1 ta được 

 y=5(a-1)+ 10 = 5a + 5

B.BÀI TẬP TỰ LUẬN

Bài 10 trang 19 SBT Toán 8 tập 2 CTST: Cho hàm số y = f(x)= 3x - 2. Tính f(-5); f(—4), f(0); f(1); f(2); f(a); f(a+1).

Giải

y=f(-5)= 3.(-5) - 2=-17

y=f(-4)= 3.(-4) - 2=-14

y=f(0)= 3.(0) - 2=-2

y=f(1)= 3.(1) - 2=1

y=f(2)= 3.(2) - 2=4

y=f(-a)= 3.(a) - 2=3a - 2

y=f(a+1)= 3.(a+1) - 2=3a + 1

Bài 11 trang 19 SBT Toán 8 tập 2 CTST: Cho hàm số $y=f(x)=\frac{2}{3}x+5$. Tìm toạ độ giao điểm của đồ thị hàm số đã cho với trục Ox và trục Oy.

Giải

Cho $y = 0  \Rightarrow x = -\frac{15}{2}$ 

Cho$ x = 0 \Rightarrow y = 5$

Đồ thị của hàm số đã cho cắt trục tung tại điểm (0; 5) và cắt trục hoành tại điểm ($-\frac{15}{2};0$)

Bài 12 trang 19 SBT Toán 8 tập 2 CTST: Cho hàm số y=f(x)=(m+1)x+5.

a) Tìm điều kiện của m để hàm số đã cho là hàm số bậc nhất.

b) Với giá trị nào của m thì đồ thị của hàm số đã cho đi qua điểm A(5; 0)?

Giải

a) Hàm số là hàm bậc nhất khi $m + 1\neq 0 \Rightarrow m \neq -1$

b) Thay A(5; 0) vào hàm số y=f(x)=(m+1)x+5.

Ta có 0 = (m+1) 5+ 5 $\Rightarrow$ m = -2  

Bài 13 trang 19 SBT Toán 8 tập 2 CTST: Cho hàm số y= (m - 3)x.

a) Với giá trị nào của m thì đồ thị của hàm số đã cho đi qua điểm A(1; 2)?

b) Với giá trị nào của m thì đồ thị của hàm số đã cho đi qua điểm B(1; -2)?

Giải

a) Thay A(1; 2) vào hàm số y= (m - 3)x 

2 = m -3 $\Rightarrow$ m = 5

b)Thay A(1; -2) vào hàm số y= (m - 3)x 

-2 = m -3 $\Rightarrow$ m = 1

Bài 14 trang 19 SBT Toán 8 tập 2 CTST: Cho hai đường thẳng d: y = x – 2 và d’:y=-2

a) Tìm hệ số góc của hai đường thẳng d và d'.

b) Tìm tọa độ giao điểm của hai đường thẳng d và d' với trục Ox và trục Oy.

c) Với giá trị nào của m thì đồ thị của hàm số y = (m - 2)x − m song song với d và cắt d'.

Giải

a) Hệ số góc của đường thẳng d là a = 1. Hệ số góc của đường thẳng d là a' =2

b) Đường thẳng d cắt trục Ox tại M(2;0), cắt trục Oy tại điểm B(0; 2).

Đường thẳng d’ ở cắt trục Ox tại điểm C$(\frac{1}{2};0)$ Cho . cắt trục Oy tại điểm D(0;1)

c) Để đồ thị của hàm số y = (m - 2)x - m song song với d, hệ số góc của hàm số này phải bằng hệ số góc của d, tức là 1. Nên ta có:

m - 2 = 1

Giải phương trình này để tìm giá trị của m:

m = 1 + 2

m = 3

Vậy, giá trị của m để đồ thị của hàm số y = (m - 2)x - m song song với d là m = 3.

Bài 15 trang 19 SBT Toán 8 tập 2 CTST: Cho đường thẳng d: y=(m– 2)x+1. Với giá trị nào của m để:

a) Đường thẳng d song song với đường thẳng $d_{1}$: y=2x+3.

b) Đường thẳng d cắt đường thẳng $d_{2}$: y=−5x+1.

Giải

a) Đường thẳng $d_{1}$ song song với đường thẳng d: y=2x+3. Hệ số $d_{1}$ bằng hệ số d bằng 2

$ m-2=2 \Rightarrow$ m = 4

b) Để đường thẳng d cắt đường thẳng $d_{2}$ 

$m -2 \neq -5 \Rightarrow m \neq -3$

Bài 16 trang 19 SBT Toán 8 tập 2 CTST: Xác định hàm số y = ax + b biết đồ thị của hàm số đã cho song song với đường thẳng y=−2x + 3 và đi qua A(1; –3).

Giải

Đồ thị  song song với đường thẳng y=−2x + 3 nên a = -2. Thay A(1; –3)  vào hàm số y = ax + b

-3= -2+b $\Rightarrow$ b =-1

Vậy hàm số có dạng y = -2x -1 

Bài 17 trang 19 SBT Toán 8 tập 2 CTST: Tìm điểm cố định mà mỗi đường thẳng d’: y= (m – 2)x + 3 luôn đi qua với mọi giá trị của m.

Giải

Đặt m = 2 khi đó  d’: y= 0x + 3 $\Rightarrow$ y = 3 

Vâyj với mọi giá trị của m , đường thẳng d’ luôn đi qua điểm (0;3)

Bài 18 trang 20 SBT Toán 8 tập 2 CTST: Cho các đường thẳng $d_{1}:y=x+1;d_{2}:y=-x-3;d_{3}y=mx+2m−1.$

a) Vẽ hai đường thẳng $d_{1}$ và $d_{2}$ trên cùng một mặt phẳng toạ độ Oxy.

b) Với giá trị nào của m thì đường thẳng $d_{3}$ trùng với đường thẳng $d_{2}$?

Giải

a)Xét đường thẳng $d_{1}$:y=x+1, cho y = 0 $\Rightarrow$ x = -1, cho x = 0  $\Rightarrow$ y = 1 

Vậy tọa độ đường thẳng $d_{1}$ (-1;1)

Tương tự ta có tọa độ đường thẳng $d_{2} (-3;-3)$

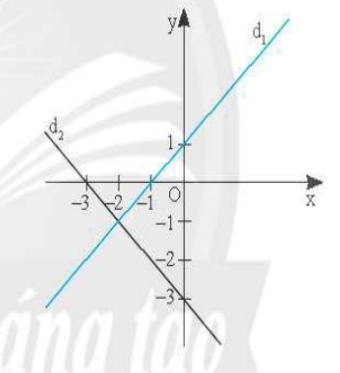
b) Để $d_{2}:y=-x-3$ trùng với $d_{3}y=mx+2m−1$.

Thì -x-3=mx+2m−1.=0

$\Rightarrow m + 1 = 0 \Rightarrow m =-1$