Bài 1 trang 68 SBT Toán 8 tập 2 CTST: Quan sát Hình 5.

a) Chứng minh rằng $\Delta HDE \sim \Delta HFD$
b) Tính độ dài HD

Giải

Tam giác HDE và tam giác HFD có:
$\widehat {DHE} =\widehat {DHF} = 90^{\circ},\widehat{E} = \widehat{HDF}$ ( cùng phụ với góc F)

$\Rightarrow \Delta HDE \sim \Delta HFD$

Vì $\Delta HDE \sim \Delta HFD$ ( cm câu a ) 

nên $\frac{EH}{HD} = \frac{HD}{HF}$,

$\Rightarrow HD^{2} = EH.HF = 9.16 = 144$

$HD = \sqrt{144} = 12$

Bài 2 trang 68 SBT Toán 8 tập 2 CTST: Quan sát hình 6, chứng minh rằng:

a) $\Delta MNP \sim  \Delta DPC$

b) $NP \perp PC$

Giải

a) Tam giác MNP vuông tại M và tam giác DPC vuông tại  có:

$\widehat{M} = \widehat {D} = 90^{\circ}. \frac{MN}{DP} = \frac{12}{8} = \frac{3}{2}, \frac{PN}{CP} = \frac{15}{10} =\frac{3}{2}$

$\Rightarrow \frac{MN}{DP} = \frac{PN}{CP}$

Do đó $\Delta MNP \sim  \Delta DPC$

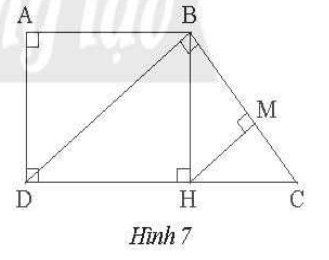
Bài 3 trang 68 SBT Toán 8 tập 2 CTST: Quan sát Hình 7, biết tứ giác ABHD là hình chữ nhật. Chứng minh rằng:

a) $BD^{2}=AB. DC$.

b) $AD^{2} = BM. BC$.

Giải

a) Vì ABHD là hình chữ nhật nên AB//DH, do đó

$\widehat{ABD} = \widehat { BDH}$  (hai góc so le trong )

Tam giác ABD và tam giác BDC có

$\widehat{A} = \widehat{ DBC} = 90^{\circ}, \widehat{ABD} = \widehat{ BDH} $( cmt)

$\Rightarrow \Delta ABD \sim \Delta BDC$ nên $\frac{AB}{BD} = \frac{BD}{DC}$

$\Rightarrow BD^{2}=AB. DC$

b) Ta có $\Delta BMH$ và $\Delta BDC$ 

$\widehat{HMB} = \widehat{BHC} = 90^{\circ}$, chung $\widehat{HBM} $

Do đó, $\Delta ABD \sim BDC$ do đó $\frac{BM}{BH} = \frac{BH}{BC}$ hay $BH^{2} = BM .BC$

Vì ABHD là hình chữ nhật nên AD = BH. Do đó $AD^{2} = BM. BC$.

Bài 4 trang 68 SBT Toán 8 tập 2 CTST: Trong Hình 8, cho tam giác BEC (BE < EC). Cho biết AC $\perp$ BD, chứng minh rằng:

a) $\Delta AIB \sim \Delta DIC$.

b) EA. EB = EC. ED.

Giải

a) Tam giác AIB và tam giác DIC có:

$\widehat{AIB} = \widehat{I} = 90^{\circ} , \frac{AI}{ID} = \frac{IB}{IC} = \frac{3}{4} \Rightarrow \frac{IA}{ID} =  \frac{IB}{IC}$

$\Rightarrow \Delta AIB \sim \Delta DIC$ 

b) Xét $ \Delta EDB$ và $ \Delta EAC$ có $\widehat{E}$ là góc chung và $\widehat{ABI} = \widehat{DCI} (  \Delta AIB  \sim \Delta DIC)$

Suy ra $ \Delta EDB \sim \Delta EAC$

Suy ra $\frac{ED}{EA} = \frac{EB}{EC}$ hay EA.EB = EC. ED

Bài 5 trang 69 SBT Toán 8 tập 2 CTST: Cho $ \Delta ABC \sim \Delta MNP$ theo tỉ số đồng dạng $k = \frac{AB}{MN} =\frac{2}{3}$. Kẻ đường ca o AH của tam giác ABC và đường cao MK của tam giác MNP.

a) Chứng minh rằng $\Delta ABH \sim \Delta MNK$. Tính tỉ số $\frac{AH}{MK}$

b) Biết diện tích tam giác ABC bằng 56 $cm^{2}$. Tính diện tích tam giác MNP.

Giải

a) Vì $\Delta ABC \sim \Delta MNP$ nên $\widehat{B} = \widehat{N}$

Tam giác ABH và tam giác MNK có:

$\widehat{AHB} = \widehat{MKN} = 90^{\circ}$

Do đó $\Delta ABH \sim \Delta MNK$ do đó $\frac{AH}{MK} = \frac{AB}{MN} =\frac{2}{3}$

b) Ta có $\Delta ABC \sim \Delta MNP$ nên $\frac{S_{\Delta ABC}}{S_{\Delta MNP}} =k^{2}$

hay $\frac{56}{S_{\Delta MNP}} =\frac{3}{2})^{2}$

Vậy $S_{\Delta MNP}= 126 (cm^{2})$

Bài 6 trang 69 SBT Toán 8 tập 2 CTST: Người ta dùng một gương phẳng để đo chiều cao của một căn nhà (Hình 9). Đặt tấm gương nằm trên mặt phẳng nằm ngang (điểm C), mắt của người quan sát nhìn thẳng vào tấm gương, người quan sát lùi dần cho đến khi nhìn thấy ảnh của đỉnh căn nhà trong gương. Cho biết $\widehat{ACB} = \widehat{MCN}$, AB = 1,65 m,BC = 4m, NC = 20 m. Tính chiều ao MN của căn nhà.

Giải

Tam giác ABC và tam giác MNC có:

$\widehat{B} =\widehat{N}=90^{\circ}, \widehat{ACB}=\widehat{MCN}$ nên $\Delta ABC \sim \Delta MNC$ 

$\Rightarrow \frac{AB}{MN} =\frac{BC}{NC}$ hay $\frac{1,65}{MN}= \frac{4}{20}$ 

Vậy MN = 8,25 m 

Bài 7 trang 69 SBT Toán 8 tập 2 CTST: Cho tam giác ABC vuông tại A. Tia phân giác của A cắt cạnh huyền BC tại M. Qua M kẻ đường thẳng vuông góc với BC và cắt AC tại N. Chứng minh rằng:
a) $\Delta MNC \sim \Delta ABC$.
b) MN = MB.

Giải

a) Tam giác MNC và tam giác ABC có:

$\widehat{NMC} = \widehat{BAC} = 90^{\circ}, \widehat{C} $ chung

Do đó $\Delta MNC \sim \Delta ABC$

b) Vì $\Delta MNC \sim \Delta ABC$ nên $\frac{MN}{AB} =\frac{MC}{AC}$ (1)

Vì AM là tia phân giác của góc BAC trong tam giác ABC nên theo tính chất đường phân giác của tam giác ta có:
$\frac{MB}{MC} = \frac{AB}{AC}$ hay $\frac{MB}{AB} =\frac{MC}{AC}$ (2) 

Từ (1) và (2) ta có 

$\frac{MN}{AB} = \frac{MB}{AB}$. Vậy MN = MB

Bài 8 trang 69 SBT Toán 8 tập 2 CTST: Cho tam giác ABC vuông tại A (AB<AC) và kẻ đường cao AH. Tia phân giác của $\widehat{B}$ cắt AC tại E và cắt AH tại F. Chứng minh rằng:

a) AB. HF AE. HB

b) AE=AF

c) $ AE^{2} = EC. FH$.

Giải

a) Tam giác ABE và tam giác HBF có:

$\widehat{BAE} = \widehat{FHB} = 90^{\circ}, \widehat{ABE} = \widehat{HBF}$  (vì BF là tia phân giác của góc ABC) nên $\Delta ABE \sim \Delta HBF$ 

$\Rightarrow \frac{AB}{HB} = \frac{AE}{HF}$ do đó AB. HF AE. HB

b) Vì $\Delta ABE \sim \Delta HBF$  nên $\widehat{AEB} = \widehat{HFB}$

Mà $\widehat{HFB} = \widehat{AFE}$ ( hai góc đối đỉnh ) nên $\widehat{AEB} = \widehat{AFE}$

Do đó, tam giác AEF cân tại A. Suy ra AE = AF

c) c) Vì BF là tia phân giác của góc ABH trong tam giác ABH nên theo tính chất đường phân giác của tam giác ta có:

$\frac{FH}{AF} = \frac{BH}{AB}$

Vì BE là tia phân giác của góc ABC trong tam giác ABC nên theo tính chất đường phân giác của tam giác ta có:

$\frac{AE}{EC} =\frac{AB}{BC}$

Mặt khác $\Delta ABH \sim \Delta CBA$ nên $\frac{AB}{BC} =\frac{BH}{AB}$

Do đó $\frac{AE}{EC} =\frac{FH}{AF}$

Suy ra AE . AF = EC . FH. Mà AE = AF nê $ AE^{2} = EC.FH$