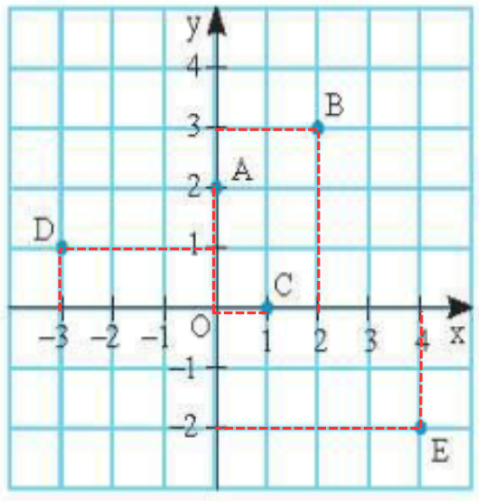
Bài 1 trang 10 SBT Toán 8 tập 2 CTST: Tìm toạ độ của các điểm A, B, C, D, E trong Hình 8.

Giải

A (0;2)

B (2;3)

C (1;0)

D (-3;1)

E (4;-2)

Bài 2 trang 10 SBT Toán 8 tập 2 CTST: Cho hình vuông ABCD có tọa độ của các điểm A(1; 2), B(4; 2), C(4; 5). Trên mặt phẳng tọa độ Oxy, hãy vẽ hình vuông ABCD và cho biết toạ độ đỉnh D.

Giải

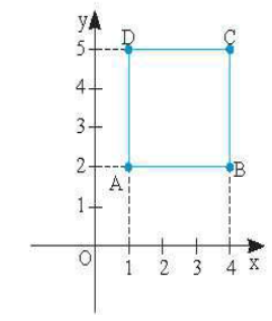
Hình vuông ABCD được biểu diễn trên mặt phẳng toạ độ Oxy như hình bên.

Toạ độ điểm D là (1; 5).

Bài 3 trang 10 SBT Toán 8 tập 2 CTST: Xác định toạ độ của các điểm sau:

a) Điểm M nằm trên trục tung và có tung độ là 3.

b) Điểm N nằm trên trục hoành và có hoành độ là –6.

c) Điểm O là gốc toạ độ.

Giải

a) M(0:3) 

b) N(-6;0)

c) O ( 0;0)

Bài 4 trang 10 SBT Toán 8 tập 2 CTST: Vẽ hệ trục toạ độ Oxy và đánh dấu các điểm A(2; 3), B(2; −1), C(−3; 3). Tam giác ABC là tam giác gì? Tỉnh diện tích của tam giác ABC.

Giải

Tam giác ABC là tam giác vuông tại A như hình bên.

Diện tích tam giác ABC 

$S_{ABC} = \frac{1}{2}AB . AC = \frac{1}{2}.4.5 =10 $

Bài 5 trang 10 SBT Toán 8 tập 2 CTST: 

a) Tìm toạ độ của các điểm M, N, P, Q trong Hình 9.

b) Em có nhận xét gì về vai trò của tia phân giác của góc $\widehat{xOy}$ so với hai đường thẳng MN, PQ?

Giải

a) M(3; 2), N(2; 3), P(-2; 0), Q(0; -2).

b) Các đoạn thẳng MN và PQ đều nhận tia phân giác của xOy làm trục đối xứng.

Bài 6 trang 10 SBT Toán 8 tập 2 CTST: Tìm toạ độ của các điểm A, B, C, D, E và F trong Hình 10.

Giải 

A(-4; 3), B(0; 3), C(-1; 0), D(-3; -3),E(1;-2), F(3; 1).

Bài 7 trang 10 SBT Toán 8 tập 2 CTST: Trên mặt phẳng toạ độ Oxy, cho toạ độ

của các điểm A(3; −1), B(2; 5), C(4; 1) và D(–4; −4). Tìm toạ độ của các điểm A’, B', C' và D’ sao cho trục hoành là đường trung trực của AA', BB', CC' và DD'.

Giải

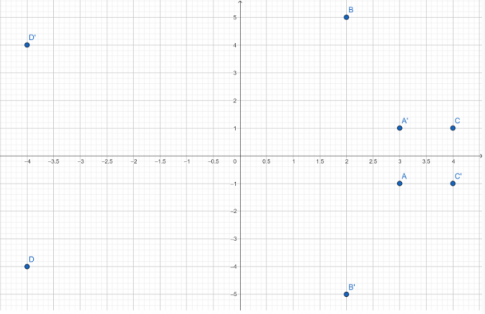
A'(3; 1), B'(2;-5), C'(4; -1), D'(-4; 4).

Bài 8 trang 10 SBT Toán 8 tập 2 CTST: Vẽ đường thẳng qua hai điểm A(0; 5) và B(–3; 5). Em có nhận xét gì về tung độ của các điểm trên đường thẳng AB?

Giải

Các điểm trên đường thẳng AB đều có tung độ bằng 5 như hình vẽ.

Bài 9 trang 10 SBT Toán 8 tập 2 CTST: Các điểm A(–3; 8), B(–2; −5), C(1; 0) và D $(\frac{1}{2};\frac{3}{4}$) có thuộc đồ thị hàm số $y=x^{2} − 1$ hay không? Vì sao?

Giải

Thay x = -3 vào $y = x^{2} -1 $ ta được $y=(−3)^{2} −1=8$. Do đó điểm A(3; 8) thuộc đồ thị của hàm số $y=x^{2}-1$.

Thay x = −2 vào $y = x^{2} − 1$ ta được $y = (-2)^{2} −1=3  \neq  -5$. Do đó điểm B(–2; −5) không thuộc đồ thị của hàm số $y=x^{2}-1$.

Thay x = 1 vào $y = x^{2} − 1$ ta được $y = 1^{2} − 1 = 0$. Do đó điểm C(1; 0) thuộc đồ thị của hàm số $y=x^{2}-1$

Thay $x = \frac{1}{2} $ vào $y = x^{2} - 1$ ta được $y = (\frac{1}{2})^{2} -1 = \frac{1}{4} -1$

$=-\frac{3}{4} \neq \frac{3}{4}$. Do dó điểm D$(\frac{1}{2} ; \frac{3}{4})$ không thuộc đồ thị của hàm số $y = x^{2} -1 $