BÀI 3. TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC

1. TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC

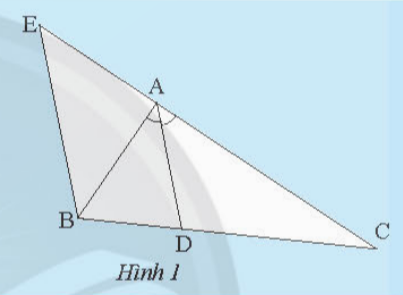
Bài 1: Cho tam giác ABC có đường phân giác AD. Vẽ đường thẳng qua B song song với AD và cắt đường thẳng AC tại E (Hình 1). Hãy giải thích tại sao:

a) tam giác BAE cân tại A

b)

Giải nhanh: 

a) Ta có: BE // AD suy ra ,

AD là tia phân giác góc nên  Do đó: => tam giác BAE cân tại A

b) Xét tam giác BCE có , theo định lí Thales ta có:  

Mà AE = AB Do đó:   

2. ÁP DỤNG TÍNH CHIA TỈ LỆ CỦA ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC

Bài 1: Tính độ dài cạnh MQ của tam giác MPQ trong Hình 6

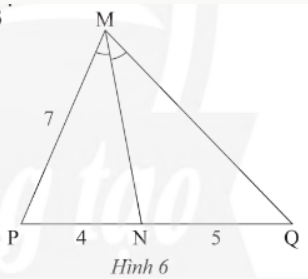
Giải nhanh: 

MN là đường phân giác góc M, suy ra nên =>

BÀI TẬP CUỐI SGK

Bài 1: Tính độ dài x trong Hình 7

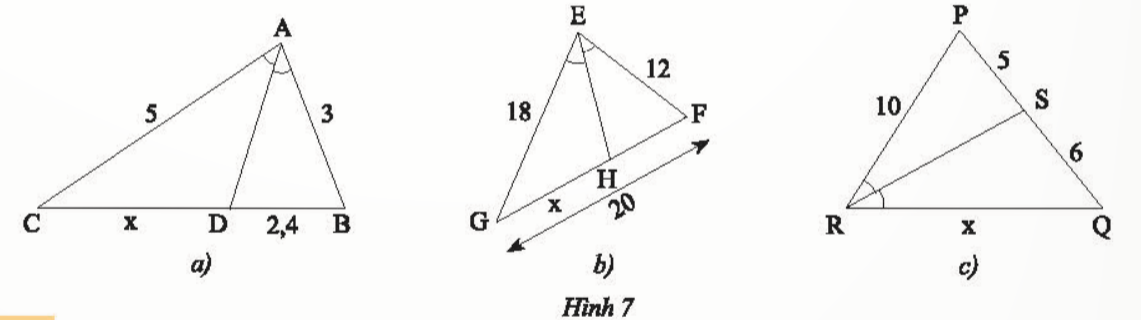
Giải nhanh: 

a) AD là đường phân giác góc A suy ra ⬄ ⬄

b) EH là đường phân giác góc E, suy ra ⬄ ⬄

c) RS là đường phân giác góc R, suy ra ⬄ ⬄ x = 12

Bài 2: Tam giác ABC có AB = 6cm, AC = 8 cm, BC = 10 cm. Đường phân giác của góc BAC cắt cạnh BC tại D

a) Tính độ dài các đoạn thẳng DB và DC

b) Tính tỉ số diện tích giữa ΔADB và ΔADC

Giải nhanh: 

a) Tam giác ABC có AD là đường phân giác

Mà ;  

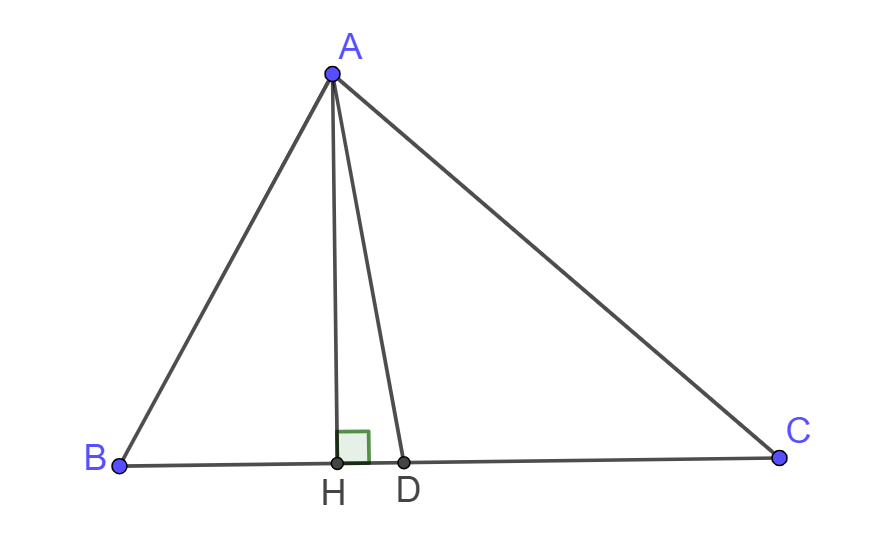
b) Vẽ tại H   .

Bài 3: Tam giác ABC có AB = 15cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt BC tại D. Qua D vẽ DE // AB (E∈AC)

a) Tính độ dài các đoạn thẳng DB, DC và DE

b) Chứng minh ABC là tam giác vuông. Tính diện tích tam giác ABC

c) Tính diện tích các tam giác ADB, ADE và DCE

Giải nhanh: 

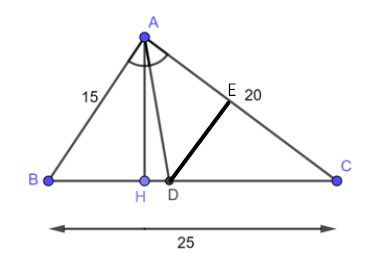
a) AD là đường phân giác góc BAC Suy ra:  

Mà Nên

Suy ra: => Nên:

Do đó, (cm)

Xét tam giác ABC có DE // AB: => => .

b) Xét tam giác ABC: AB = 15 cm, AC = 20 cm, BC = 25cm, nên 

suy ra tam giác ABC vuông tại A

c) Kẻ ta có:  

Suy ra =>

 .

Bài 4: Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Đường phân giác của góc A cắt BC tại D.

a) Tính BC, DB, DC

b) Vẽ đường cao AH. Tính AH, HD và AD

Giải nhanh: 

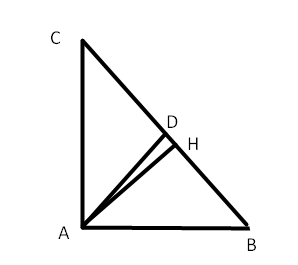
a) Tam giác ABC vuông tại A: =>

AD là tia phân giác góc A nên

(cm)

b) Ta có: (cm)

Tam giác ABH vuông tại H nên (cm)

Ta có: (cm)

Tam giác ADH vuông tại H nên: 

Bài 5: Cho tam giác ABC có trung tuyến AM. Đường phân giác của góc AMB cắt AB tại D và đường phân giác của góc AMC cắt AC tại E (Hình 8). Chứng minh DE // BC 

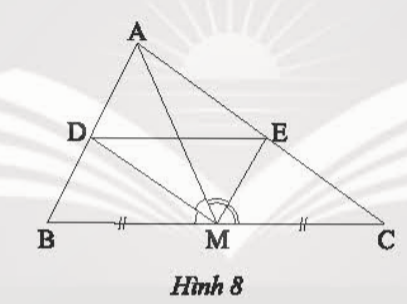
Giải nhanh: 

MD là đường phân giác góc AMB suy ra

ME là đường phân giác góc AMC suy ra  

Mà MB = MC, do đó: = => DE // BC.