CÂU HỎI TRẮC NGHIỆM

Đáp án:

BÀI TẬP TỰ LUẬN

Bài tập 8 trang 89 sgk Toán 8 tập 1 CTST

Cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC...

Đáp án:

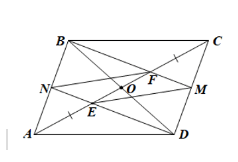
a) 

Gọi O là giao điểm của AC và BD => $AO=CO= \frac{1}{2}AC$ (1) 

$CF=FE=EA= \frac{1}{3}AC$ (1)

Từ (1) và (2) suy ra

$\frac{CF}{CO}=\frac{\frac{1}{3}AC}{\frac{1}{2}AC}= \frac{2}{3} ⬄ CF= \frac{2}{3}CO$

Xét ∆BDC có: CO là trung tuyến của tam giác ; $CF = \frac{2}{3}CO$

F là trọng tâm => BM là đường trung tuyến => M là trung điểm của CD.

Chứng minh tương tự ta có E là trọng tâm của ∆ABD

=> DN là đường trung tuyến N là trung điểm của AB.

b) $NB= \frac{1}{2}AB ; MD=\frac{1}{2}CD$; AB = CD => NB = MD 

Xét tứ giác BMDN có: NB // MD , NB = MD => BMDN là hình bình hành.

$\Rightarrow$ MB = ND ; MB // ND

$\Rightarrow FM= \frac{1}{3}BM, EN= \frac{1}{3}DN$

=> EN = FM. 

Xét tứ giác NFME có: NE // MF ; EN = MF => EMFN là hình bình hành.

Bài tập 9 trang 89 sgk Toán 8 tập 1 CTST

Cho tam giác ABC cân tại A. Gọi H, D lần lượt là trung điểm của các cạnh BC và AB...

Đáp án:

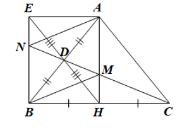
a) ∆ABC cân tại A => AH vừa là đường trung tuyến vừa là đường trung trực

⇒ AH⊥BC.

Xét ∆AHB vuông tại H có: $HD=BD=AD=\frac{1}{2}AB$ => ∆DHB cân tại D.

=> $\widehat{DHB} = \widehat{DBH}$

Mà $\widehat{ACB} = \widehat{ABC}$

⇒ $\widehat{DHB} = \widehat{ACB}$  => DH // AC => ADHC là hình thang.

b) Xét tứ giác EAHB có: EH và AB cắt nhau tại H là trung điểm mỗi đường

EAHB là hình bình hành.

Mà $\widehat{BHA} =90°$  EAHB là hình chữ nhật.

c) EAHB là hình chữ nhật HM // EN => $\widehat{NED} = \widehat{MHD}$

Xét ∆NDE và ∆MDH có:

$\widehat{EDN} = \widehat{HDM}$

DE = DH

$\widehat{NED} = \widehat{MHD}$

∆NDE = ∆MDH (g.c.g) => ND = MD

Xét tứ giác NAMB có: MN cắt AB tại M là trung điểm mỗi đường 

$\Rightarrow$ NAMB là hình bình hành.

Bài tập 10 trang 89 sgk Toán 8 tập 1 CTST

Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của...

Đáp án:

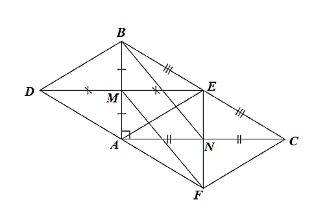
a) Xét ∆ABC vuông tại A có: AE = EC => E thuộc đường trung trực của AC.

N là trung điểm của AC => N nằm trên đường trung trực của AC.

EN là đường trung trực AC => EN⊥AC

=> AB // EN ( cùng AC ) => ABEN là hình thang

Mà $\widehat{BAN}=90°$  => ABEN là hình thang vuông.

b) M là trung điểm của AB M nằm trên đường trung trực của AB.

EA = EB => E nằm trên đường trung trực của AB.

ME là đường trung trực của AB ⇒ EM ⊥ AB, 

Xét tứ giác MENA có: $\widehat{ANE} = \widehat{MAN} = \widehat{AME} =90°$

⇒ MENA là hình chữ nhật.

c) Xét tứ giác BNFM có: BM // FN , MF // BN => BNFM là hình bình hành

=>MB = NF.

Mà AM = EN , AM = BM => NF = EN

Xét tứ giác AECF có: FE cắt AC tại N là trung điểm mỗi đường

⇒ AECF là hình bình hành.

Mà AC ⊥ EF ⇒ AECF là hình thoi.

d) Hình thoi AECF => FA = EC ; FA // EC

Chứng minh tương tự ta có BEAD là hình thoi => BE // AD 

Ta có  AD // BC , AF // BC => AD ≡ AF => 3 điểm D, A, F thẳng hàng (1)

Ta có :  CE = AF , BE = AD , CE = BE  AF = AD (2)

Từ (1) và (2) => A là trung điểm của DF (đpcm).

Bài tập 11 trang 89 sgk Toán 8 tập 1 CTST

Cho hình bình hành ABCD có AB = 2AD. Gọi E, F lần lượt là trung điểm của AB và CD...

Đáp án:

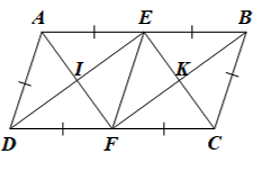
a) Xét tứ giác AECF có: AE // FC , AE = FC => AECF là hình bình hành.

b) Xét tứ giác ADFE có: AE // DF , AE = DF => ADFE là hình bình hành

Mà AB = 2.AD => $AD=AE=\frac{1}{2}AB$ => ADFE là hình thoi.

c) ADFE là hình thoi => AF ⊥ DE ⇒ $\widehat{EIF}=90°$

ED là đường phân giác của $\widehat{FEA}$ ⇒ $\widehat{FED} = \frac{1}{2}\widehat{FEA}$

Chứng minh tương tự ta có tứ giác EBCF là hình thoi

EC ⊥ BF suy ra $\widehat{FKE}=90°$

EC là đường phân giác của $\widehat{BEF}$

$\Rightarrow \widehat{CEF} = \frac{1}{2}\widehat{BEF}$.

$\widehat{IEK} = \widehat{DEF} + \widehat{CEF}$

$= \frac{1}{2}(\widehat{AEF} + {BEF}) = \frac{1}{2} .180^{\circ}= 90^{\circ}$

Xét tứ giác IEKF có: $\widehat{EIF} = \widehat{FKE} = \widehat{IEK}=90°$

⇒ IEKF là hình chữ nhật.

d) Để tứ giác IEKF là hình vuông thì EI = IF   (1)

Xét hình thoi AEFD có: AI = IF , ID = EI    (2)

Từ (1) và (2) => AI = ID

Xét ∆ADI có: AI = ID => ∆ADI cân tại I

Mà $\widehat{AID} =90°$

=> ∆ADI vuông cân tại I => $\widehat{IAD}=45°$

AEFD là hình thoi => $\widehat{EAD} = \widehat{IAD}.2 =45°.2=90°$ Vậy cần thêm điều kiện $\widehat{BAD}=90°$ 

hay ABCD là hình chữ nhật.

Bài tập 12 trang 89 sgk Toán 8 tập 1 CTST

Cho hình bình hành ABCD...

Đáp án:

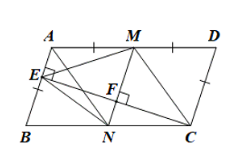
a) AB // MN ( cùng  CE )

MN // CD ( cùng // AB)

Tứ giác MDCN có: MD // CN , MN // CD => MDCN là hình bình hành.

$MA=MD=\frac{1}{2}AD;  AD = 2.AB => AB = MD$

Mà AB = CD => MD = DC => MDCN là hình thoi.

b) MDCN là hình thoi $MD=DC=CN=NM=AD= \frac{1}{2}BC$

Xét ∆ECB vuông tại E có:  $EN=BN=CN=\frac{1}{2}BC$

NE = NC => N nằm trên đường trung trực của EC

FN⊥EC => NF là đường trung trực của đoạn thẳng EC.

F là trung điểm của EC 

∆MFC = ∆MFE (hai cạnh góc vuông) 

=> MC = ME => ∆CME cân tại M.

c) MN // AB => $\widehat{EMF} = \widehat{AEM}$

∆MFC = ∆MFE (cmt) =>  $\widehat{CMF} = \widehat{EMF}$

$\Rightarrow \widehat{AEM} = \widehat{CMF}$

MDCN là hình thoi MC là đường phân giác của $\widehat{DMN}$

=> $\widehat{CMF}= \frac{1}{2}\widehat{DMN}$

$\widehat{AEM}= \widehat{CMF} = \frac{1}{2}\widehat{DMN}. (1)$

MDCN là hình thoi => $\widehat{DCN}=\widehat{DMN}$

ABCD là hình bình hành $\widehat{DCB} = \widehat{DAB}$

$\Rightarrow \widehat{DMN}= \widehat{DAB} (2)$

Từ (1) và (2) => $\widehat{AEN} = {1}{2}\widehat{DAB} \Rightarrow \widehat{DAB} = 2\widehat{AEM} (dpcm)$