1. PHƯƠNG PHÁP ĐẶT NHÂN TỬ CHUNG

Hoạt động 1 trang 23 sgk Toán 8 tập 1 CTST

Tính diện tích của nền nhà có bản vẽ ...

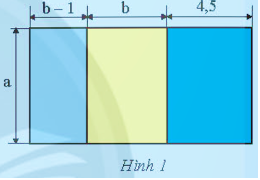
Đáp án:

Cách 1: $S = a . (b - 1) + a . b + a . 4,5(m^2)$ 

Với $a = 5; b = 3,5 => S = 5 . (3,5 – 1) + 5 . 3,5 + 4,5 . 5 = 52,5 (m^2)$ 

Cách 2 : $S = a. (b – 1 + b + 4,5) = a. (2b + 3,5) ( m^2)$

Với $a = 5; b = 3,5 => S = 5 . (2 . 3,5 + 3,5) = 52,5 (m^2)$.

Cách 2 tính nhanh hơn.

Thực hành 1 trang 24 sgk Toán 8 tập 1 CTST

Phân tích các đa thức sau thành nhân tử...

Đáp án:

a) $P = 6x − 2x^3 = 2x×3 − 2x×x^2 = 2x(3−x^2)$

b) $Q = 5x^3 − 15x^2y = 5x^2 × x − 5x^2 × 3y = 5x^2(x − 3y)$

c) $R=3x^3y^3 − 6xy^3z + xy = xy × 3x^2y2 − xy × 6y^2z + xy$

= $xy(3x^2y^2 − 6y^2z + 1)$

2. PHƯƠNG PHÁP SỬ DỤNG HẰNG ĐẲNG THỨC

Hoạt động 2 trang 24 sgk Toán 8 tập 1 CTST

Tìm biểu thức thích hợp thay vào mỗi chỗ...

Đáp án: 

a) $4x^2 − 9 = (2x)^2 − (3)^2 = (2x + 3)(2x - 3)$

b) $x^2y^2 − y^2 = (xy)^2 - (\frac{1}{2}y)^2$ 

= $(xy - \frac{1}{2}y)(xy + \frac{1}{2}y)$

Thực hành 2 trang 24 sgk Toán 8 tập 1 CTST 

Phân tích các đa thức sau thành nhân tử...

Đáp án:

a) $x^3 + 4x = x(x^2 + 4)$

b) $6ab − 9ab^2 = 3ab(2 − 3b)$

c) $2a(x − 1) + 3b(1 − x) = 2a(x − 1) − 3b(x − 1) = (2a − 3b)(x − 1)$

d) $(x − y)^2 − x(y − x) = (x−y)^2 + x(x − y)$

= (x − y + x)(x − y) = (2x - y)(x - y)

Vận dụng 1 trang 24 sgk Toán 8 tập 1 CTST 

Tìm một hình hộp chữ nhật có thể tích $2x^3 − 18x$ (với $x > 3$) mà độ dài các cạnh đều là biểu thức chứa x

Đáp án:

Ta có: $2x^3 − 18x = 2x(x^2 − 9) = 2x(x − 3)(x + 3)$

Vậy hình hộp chữ nhật có độ dài ba kích thước là $2x, x + 3$ và $x - 3$.

Vận dụng 2 trang 24 sgk Toán 8 tập 1 CTST

Giải đáp câu hỏi trang 23

Đáp án:

Ta có: $99^3 – 99 = 99.(99^2 – 1) = 99.(99 + 1).(99 - 1) = 99.100.98$

suy ra $(99^3 – 99) ⁝ 98, 99$ và $100$.

$n^3 – n = n(n^2 – 1) = n.(n +1).(n - 1)$

Vì vậy $n^3 − n$ chia hết cho $n, n - 1$ và $n + 1$ (n là số tự nhiên, n > 1)

Vậy phát biểu của hai bạn đều đúng.

3. PHƯƠNG PHÁP NHÓM HẠNG TỬ

Hoạt động 3 trang 24 sgk Toán 8 tập 1 CTST

Hãy hoàn thành biến đổi sau vào vở...
Đáp án:

$a^2 + ab + 2a + 2b = (a^2 + ab) + (2a + 2b)$

= $a(a + b) + 2(a + b) = (a + b)(a + 2)$.

Ta có thể biến đổi theo cách khác như sau:

$a^2 + ab + 2a + 2b = (a^2 + 2a) + (ab + 2b)$

= $a(a + 2) + b(a + 2) = (a + 2)(a + b)$.

Thực hành 3 trang 25 sgk Toán 8 tập 1 CTST 

Phân tích các đa thức sau thành nhân tử...

Đáp án:

a) $a^3 − a^2b + a − b = (a^3 + a) − (a^2b + b)$

= $a(a^2 + 1) − b(a^2 + 1) = (a−b)(a^2 + 1)$

b) $x^2 – y^2 + 2y – 1= x^2 – (y^2 – 2y + 1)$

= $x^2 – (y–1)^2 = (x + y – 1) . [x – (y – 1)]$

= $(x + y – 1)(x – y + 1)$.

Vận dụng 3 trang 25 sgk Toán 8 tập 1 CTST

Có thể ghép bốn tấm pin mặt trời với kích thước như...

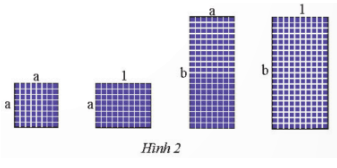
Đáp án:

Tổng diện tích bốn tấm pin mặt trời là:

$S = a^2 + a + ab + b  = (a + b)(a + 1) (m^2)$.

Có thể ghép bốn tấm pin mặt trời thành hình chữ nhật có chiều dài là $a + b (m)$, chiều rộng là $a + 1(m)$ 

Với $a = 0,8 (m)$ và $b = 2 (m)$ ta có:

Chiều dài hình chữ nhật đó là: $0,8 + 2 = 2,8(m)$.

Chiều rộng hình chữ nhật đó là: $0,8 + 1 = 1,8(m)$.

Diện tích hình chữ nhật đó là: $2,8.1,8 = 5,04 (m^2)$.

BÀI TẬP CUỐI SGK 

Bài tập 1 trang 25 sgk Toán 8 tập 1 CTST

Phân tích các đa thức sau thành nhân tử...

Đáp án:

a) $x^3 + 4x = x(x^2 + 4)$.

b) $6ab − 9ab^2 = 3ab(2 − 3b).$

c) $2a(x − 1) + 3b(1 − x) = 2a(x − 1) − 3b(x − 1) = (2a − 3b)(x − 1)$

d) $(x − y)^2 − x(y − x) = (x − y)^2 + x(x − y)$

= $(x − y + x)(x − y)$ = $(2x − y)(x − y)$

Bài tập 2 trang 25 sgk Toán 8 tập 1 CTST 

Phân tích các đa thức sau thành nhân tử...

Đáp án:

a) $4x^2 − 1 = (2x)^2 − 1 = (2x − 1)(2x + 1)$

b) $(x+2)^2 − 9 = (x+2)^2 − 3^2 = (x + 2 − 3)( x + 2 + 3) = (x−1)(x+5)$

c) $(a+b)^2 − (a−2b)^2 = (a+b−a+2b)(a+b+a−2b) = 3b(2a−b)$

Bài tập 3 trang 25 sgk Toán 8 tập 1 CTST

Phân tích các đa thức sau thành nhân tử...

Đáp án:

a) $4a2+4a+1 = (2a)^2+2×2a+1 = (2a+1)^2$

b) $−3x^2+6xy−3y^2$

= $−[(\sqrt{3}x)^2 −2 × \sqrt{3}x . \sqrt{3}y +(\sqrt{3}y)^2]$

= $−(\sqrt{3}x - \sqrt{3}y)^2 = −3(x−y)^2$

c) $(x+y)^2 − 2(x+y)z + z^2 = (x+y−z)^2$

Bài tập 4 trang 25 sgk Toán 8 tập 1 CTST

Phân tích các đa thức sau thành nhân tử...

Đáp án:

a) $8x^3 − 1 = (2x)^3 − 1 = (2x−1)[(2x)^2 + 2x + 1]$

 = $(2x−1)(4x^2 + 2x + 1)$

b) $x^3 + 27y^3 = x^3 + (3y)^3 = (x+3y)(x^2 − 3xy + 9y^2)$

c) $x^3 − y^6 = x^3 − (y^2)^3 = (x−y^2)(x^2 + xy^2 + y^4)$

Bài tập 5 trang 25 sgk Toán 8 tập 1 CTST

Phân tích các đa thức sau thành nhân tử...

Đáp án:

a) $4x^3 − 16x = 4x(x^2 − 4) = 4x(x−2)(x+2)$

b) $x^4 − y^4 = (x^2 − y^2)(x^2 + y^2) = (x−y)(x+y)(x^2 + y^2)$

c) $xy^2 + x^2y + \frac{1}{4}y^3 = y(xy + x^2 + \frac{1}{4}y^2)$

= $y(x + \frac{1}{2}y)^2$

d) $x^2 + 2x − y^2 + 1 = (x^2 + 2x + 1) − y^2$

= $(x+1)^2 − y^2 = (x+1−y)(x+1+y)$

Bài tập 6 trang 25 sgk Toán 8 tập 1 CTST

Phân tích các đa thức sau thành nhân tử...

Đáp án:

a) $x^2 − xy + x − y = (x^2 − xy) + (x − y)$

= $x(x−y) + (x−y) = (x+1)(x−y).$

b) $x^2 + 2xy − 4x − 8y = (x^2 − 4x) + (2xy − 8y)$

= $x(x − 4) + 2y( x−4) = (x + 2y)(x − 4)$

c) $x^3 − x^2 − x + 1= (x^3 + 1) − (x^2 + x)$

= $(x+1)(x^2 − x + 1) − x(x + 1) = (x+1)(x^2 − 2x + 1)$

= $(x−1)^2(x+1)$

Bài tập 7 trang 25 sgk Toán 8 tập 1 CTST

Cho y > 0. Tìm độ dài cạnh của hình vuông có diện tích bằng...

Đáp án:

 Ta có : $49y^2 + 28y + 4 = (7y)^2 + 2×7y×2 + 22 = (7y+2)^2$

Vậy cạnh của hình vuông bằng $7y + 2$