1. TỨ GIÁC

Hoạt động 1 trang 63 sgk Toán 8 tập 1 CTST

Trong các hình tạo bởi bốn đoạn thẳng...

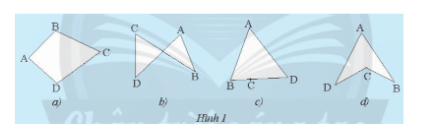
Đáp án:

Hình a), b), d) 

Hoạt động 2 trang 64 sgk Toán 8 tập 1 CTST

Vẽ các đường thẳng lần lượt chứa...

Đáp án:

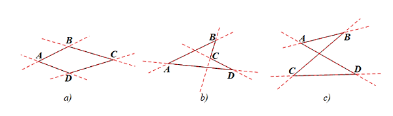
Nhận xét :

Hình a : tứ giác luôn nằm trong cùng một phần mặt phẳng được phân chia bởi đường thẳng chứa bất kì cạnh nào của tứ giác.

Hình b, c : tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC.

Thực hành 1 trang 65 sgk Toán 8 tập 1 CTST

Vẽ tứ giác MNPQ và tìm...

Đáp án:

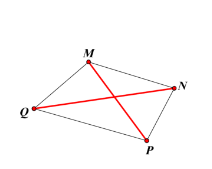
Hai đỉnh đối nhau: Q và N ; P và M 

Hai đường chéo: QN và PM 

Hai cạnh đối nhau: QP và MN ; QM và PN

Vận dụng 1 trang 65 sgk Toán 8 tập 1 CTST

Tìm các đỉnh, cạnh và đường chéo của tứ giác Long Xuyên...

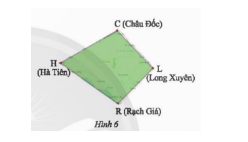
Đáp án:

Các đỉnh: C, H, R, L 

Các cạnh: HR, HC, LC, RL

Các đường chéo: LH và CR.

2. TỔNG CÁC GÓC CỦA MỘT TỨ GIÁC

Hoạt động 3 trang 65 sgk Toán 8 tập 1 CTST

Đường chéo AC chia tứ giác...

Đáp án:

Xét $\Delta ABC$ có: 

$\widehat{ABC} + \widehat{BCA} + \widehat{CAB} = 180^ {\circ}$

Xét $\Delta ADC$ có : 

$widehat{ACD} + \widehat{ADC}+ \widehat{DAC} = 180^{\circ}$

$\Rightarrow \widehat{ABC} + \widehat{BCA} + \widehat{CAB} + \widehat{ACD} + \widehat{ADC}+ \widehat{DAC} = 180^ {\circ} + 180^ {\circ}$

$\Rightarrow \widehat{ABC} + \widehat{BCD} + \widehat{ADC} + \widehat{DAB} = 360^{\circ}$

Thực hành 2 trang 66 sgk Toán 8 tập 1 CTST

Tìm x trong mỗi tứ giác sau...

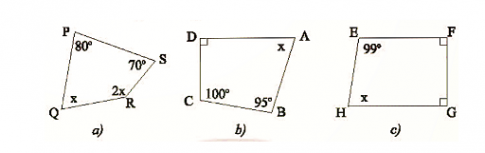
Đáp án:

a) $80^{\circ}+ x+2x+70^{\circ} = 360^{\circ}$

$\Leftrightarrow 3x =210^{\circ} \Leftrightarrow x = 70^{\circ}$

b) $90^{\circ} +x+95^{\circ}+100^{\circ}-360^{\circ}$

 $\Leftrightarrow x = 75^{\circ}$ 

c) $99^{\circ} +x+90^{\circ} .2 = 360^{\circ}$

$\Leftrightarrow x = 81^{\circ}$

Vận dụng 2 trang 66 sgk Toán 8 tập 1 CTST

Phần thân của cái diều ở Hình 10a được vẽ lại như...

Đáp án:

Xét $\Delta ACD$ và $\Delta ACB$  có: AD = AB ; chung cạnh AC ; CD = BC 

$\Rightarrow \Delta ACD = \Delta ACB (c.c.c)$

$\Rightarrow \widehat{ADC} = \widehat{ABC}$

Xét tứ giác $ABCD$ có:

$\widehat{ADC} = \widehat{ABC} = [(360^{\circ} - (130^{\circ} + 60^{\circ})] : 2 = 85^{\circ}$

BÀI TẬP CUỐI SGK

Bài tập 1 trang 66 sgk Toán 8 tập 1 CTST 

Tìm số đo các góc chưa biết của tứ giác trong...

Đáp án:

a) $\widehat{B} = 360^{\circ}-(110^{\circ}+75^{\circ}.2) = 100^{\circ}$

b) $\widehat{M} = 360^{\circ} - (90^{\circ}.2 + 70^{\circ}) = 110^{\circ}$

c) $\widehat{TSV} = 180^{\circ} - 60^{\circ} = 120^{\circ}$

$\widehat{V} = 360^{\circ} - (115^{\circ} +120^{\circ} +65^{\circ})$ 

= $60^{\circ}$

d) $\widehat{F} = 360^{\circ} - (80^{\circ} + 100^{\circ} +70^{\circ}) $

= $110^{\circ}$

Bài tập 2 trang 66 sgk Toán 8 tập 1 CTST

Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó...

Đáp án:

Xét tứ giác ABCD có:

$\widehat{A_2}+\widehat{B_2}+\widehat{C_2}+\widehat{D_2}$

$= 360^{\circ}$

$\widehat{A_1} + \widehat{A_2} = 180^{\circ}$

$\widehat{B_1} + \widehat{B_2} = 180^{\circ}$

$\widehat{C_1} + \widehat{C_2} = 180^{\circ}$

$\widehat{D_1} + \widehat{D_2} = 180^{\circ}$

$\Rightarrow (\widehat{A_1} +\widehat{A_2}) +(\widehat{B_1} +\widehat{B_2})+(\widehat{C_1} + \widehat{C_2}) + (\widehat{D_1}+\widehat{D_2}) = 180^{\circ} . 4 = 720^{\circ}$

$\Rightarrow \widehat{A_2} + \widehat{B_2}+ \widehat{C_2} + \widehat{D_2}) = 720^{\circ} - 360^{\circ} = 360^{\circ}$

Vậy tổng số đo bốn góc ngoài của tứ giác ABCD bằng  360^{\circ}

Bài tập 3 trang 67 sgk Toán 8 tập 1 CTST

Tứ giác ABCD có...

Đáp án:

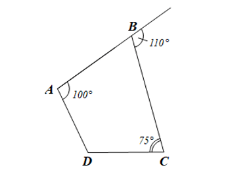
$\widehat{ABC} = 180^{\circ} - 110^{\circ} = 70^{\circ}$

$\widehat {D} = 360^{\circ} - (70^{\circ} +75^{\circ} +100^{\circ})$

$= 115^{\circ}$

Bài tập 4 trang 67 sgk Toán 8 tập 1 CTST

Tứ giác ABCD có góc ngoài tại đỉnh...

Đáp án:

Góc ngoài tại đỉnh D:

$D = 360^{\circ} - (65^{\circ} +100^{\circ} +60^{\circ}) = 135^{\circ}$

Bài tập 5 trang 67 sgk Toán 8 tập 1 CTST

Tứ giác ABCD có số đo...

Đáp án:

$\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D} = 360^{\circ}$

$\Leftrightarrow x+2x+3x+4x = 360^{\circ}$

$\Leftrightarrow 10x= 360^{\circ} \Leftrightarrow  x = 36^{\circ}$

$\Rightarrow \widehat{A}= 36^{\circ}; \widehat{B}= 72^{\circ}$;

$\widehat{C} = 108^{\circ}; \widehat{D}= 144^{\circ}$

Bài tập 6 trang 67 sgk Toán 8 tập 1 CTST 

Ta có tứ giác ABCD với...

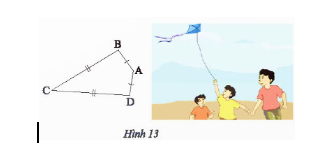
Đáp án:

a) CB = CD nên C thuộc đường trung trực của BD.

AB = AD nên A thuộc đường trung trực của BD. 

$\Rightarrow$ AC là đường trung trực của đoạn thẳng BD.

b) Xét $\Delta CDA$ và $\Delta CDA$ có: CB = CD ; chung cạnh AC ; AB = AD

$\Rightarrow \Delta CBA = \Delta CDA (c.c.c)$ 

$\Rightarrow \widehat{B} = \widehat{D} = 95^{\circ}$ 

$\widehat{A} = 360^{\circ} - ( \widehat{B}+ \widehat{C} + \widehat{D})$

$= 360^{\circ} - (95^{\circ} +35^{\circ} +95^{\circ}) = 135^{\circ}$

Bài tập 7 trang 67 sgk Toán 8 tập 1 CTST

Trên bản đồ, tứ giác BDNQ với các đỉnh là các thành phố Buôn Ma Thuột...

Đáp án:

a) Cạnh kề với cạnh BD là : BQ và DN

Cạnh đối với cạnh BD là : QN 

b) Các đường chéo là : QD; BN.