CHƯƠNG 3. ĐỊNH LÝ PYTHAGORE. CÁC LOẠI TỨ GIÁC THƯỜNG GẶP

BÀI 2. TỨ GIÁC

1. TỨ GIÁC

HĐKP1:

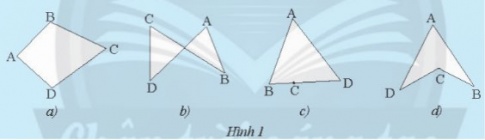
Trong các hình tạo bởi bốn đoạn thẳng AB, BC, CD và DA ở Hình 1a), b), d) không có hai đoạn thẳng cùng nằm trên một đường thẳng.

=> Kết luận:

Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD và DA, trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.

Ví dụ 1: (SGK – tr63)

Đỉnh và cạnh của tứ giác

Tứ giác ABCD còn được gọi là tứ giác DCBA, CBAD, BADC,..

Các điểm A, B, C, D gọi là các đỉnh.

Các đoạn thẳng AB, BC, CD, DA gọi là các cạnh.

Tứ giác lồi

HĐKP2:

Ta vẽ các đường thẳng lần lượt chứa mỗi cạnh của các tứ giác như hình vẽ dưới đây:

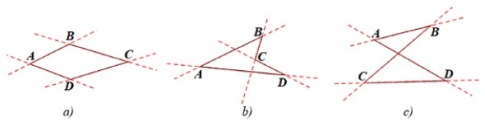
Nhận xét:

+ Hình a): các cạnh còn lại của tứ giác luôn nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa bất kì cạnh nào của tứ giác.

+ Hình b): các cạnh còn lại của tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC (hoặc CD) của tứ giác.

+ Hình c): các cạnh còn lại của tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC (hoặc AD) của tứ giác.

=> Kết luận:

Tứ giác lồi là tứ giác luôn nằm trong cùng một phần mặt phẳng được phân chia bởi đường thẳng chứa bất kì cạnh nào của tứ giác.

Ví dụ 2: (SGK – tr64)

* Chú ý: 

Từ nay, khi nói đến tứ giác mà không chú thích gì thêm, ta hiểu đó là tứ giác lồi.

Cạnh, góc, đường chéo của tứ giác

Trong một tứ giác:

a) Hai cạnh kề nhau là hai cạnh có chung một đỉnh.

VD: 

Trong hình 5, BA và BC là hai cạnh kề nhau.

b) Hai cạnh kề nhau tạo thành một góc của tứ giác.

VD: Tứ giác ABCD có các góc là DAB,ABC,BCD,CDA . Các cặp góc DABvà BCD; ABCvà CDAđược cặp góc đối.

c) Hai cạnh đối nhau là hai cạnh không có chung đỉnh nào.

VD: Trong hình 5, A và C là hai đỉnh đối nhau.

e) Đường chéo là đoạn thẳng nối hai đỉnh đối nhau.

Ví dụ: Trong hình 5, tứ giác ABCD có hai đường chéo là AC và BD.

Thực hành 1: 

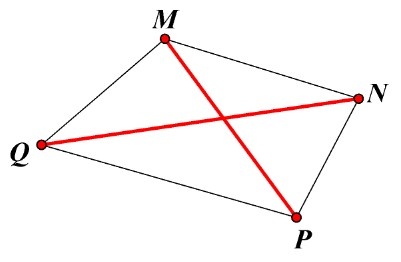
Trong tứ giác MNPQ có:

‒ Hai đỉnh đối nhau: M và P; N và Q;

‒ Hai đường chéo: MP và NQ;

‒ Hai cạnh đối nhau: MN và PQ; MQ và NP.

Vận dụng 1:

Trong tứ giác Long Xuyên CHRL có:

+ Các đỉnh: C, H, R, L;

+ Các cạnh: CH, HR, RL, LC;

+ Các đường chéo: CR và HL.

2. TỔNG CÁC GÓC CỦA MỘT TỨ GIÁC

HĐKP3.

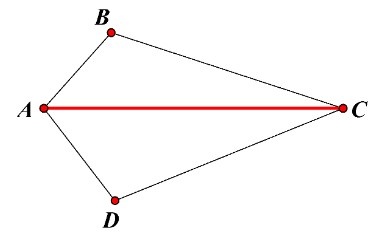
Xét tam giác ACB có:

BAC+ABC+ACB = $180^{o}$ (định lí tổng ba góc trong một tam giác).

Xét tam giác ACD có:

CAD+ACD+ADC = $180^{o}$ (định lí tổng ba góc trong một tam giác).

Do BAC+ABC+ACB+CAD++ACD+ADC = $180^{o}+180^{o}$

Suy ra BAC+CAD+ABC+ACB+ACD+ADC = $360^{o}$

Hay A+B+C+D = $360^{o}$

Vậy tổng các góc của tứ giác ABCD bằng $360^{o}$

=> Kết luận: 

Tổng số đo các góc của một tứ giác bằng $360^{o}$.

Ví dụ 3: SGK – tr65, 66

Thực hành 2. 

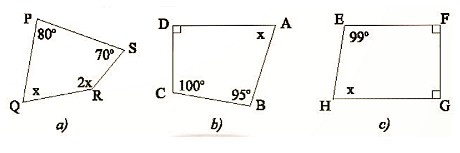
a) 

Xét tứ giác PQRS có: 

80°+70°+2x+x=360° (định lí tổng các góc của một tứ giác)

Suy ra 3x=360°–80°+70°=210°

Do đó x = 70°.

b) 

Xét tứ giác ABCD có: 

x+95°+100°+90°=360°

(định lí tổng các góc của một tứ giác)

Suy ra x = 360°–95°+100°+90°x=75°.

c)

Xét tứ giác EFGH có: 

99°+90°+90°+x=360° (định lí tổng các góc của một tứ giác)

Suy ra

 x =360°–99°+90°+90°x=81°.

Vận dụng 2. 

Xét ΔABC và ΔADC có:

AC là cạnh chung; 

AB = AD; 

BC = DC (gt).

Do đó ΔABC = ΔADC (c.c.c).

Suy ra B=D (hai góc tương ứng).

Xét tứ giác ABCD có: 

A+B+C+D = $360^{o}$ (định lí tổng các góc của một tứ giác)

Suy ra $130^{o}+B+60^{o}+B=360^{o}$

Hay 2B = $360^{o}-130^{o}+60^{o}=170^{o}$

Do đó B = $85^{o}$

Vậy B=D= $85^{o}$