1. ĐƠN THỨC VÀ ĐA THỨC

Hoạt động 1 trang 6 sgk Toán 8 tập 1 CTST

Một số biểu thức được phân chia thành các nhóm như dưới đây

a) Các biểu thức ở nhóm A có đặc điểm gì phân biệt với các biểu thức ở nhóm B và nhóm C?

b) Các biểu thức ở nhóm A và nhóm B có đặc điểm gì chung, phân biệt với các biểu thức ở nhóm C?

Đáp án:

a) - Nhóm A có các biểu thức chỉ gồm một số hoặc một tích.

    - Nhóm B và nhóm C có các biểu thức là tổng, hiệu hoặc thương.

b) - Nhóm A và B có các biểu thức là tích giữa các số và biến hoặc tổng, hiệu.

    -  Nhóm C biểu thức có phép chia và căn bậc hai. 

Thực hành 1 trang 7 sgk Toán 8 tập 1 CTST 

Cho các biểu thức sau: $ab-\pi r^{2}; \frac{4\pi r^{3}}{3}; \frac{p}{2\pi}; x-\frac{1}{y}; 0; \frac{1}{\sqrt{2}}; x^3-x+1$

Đáp án:

a) Đơn thức: $\frac{4\pi r^{3}}{3}; \frac{p}{2\pi}; 0; \frac{1}{\sqrt{2}}$

b) 

Vận dụng 1 trang 7 sgk Toán 8 tập 1 CTST 

Một bức tường hình thang có cửa sổ hình tròn với các kích thước như hình 1 (tính bằng m)

a) Viết biểu thức biểu thị diện tích bức tường (không tính phần cửa sổ)

b) Tính giá trị diện tích trên khi a = 2m; h = 3m; r = 0,5m (lấy

$\pi=3,14$ làm tròn kết quả đến hàng phần trăm).

Đáp án:

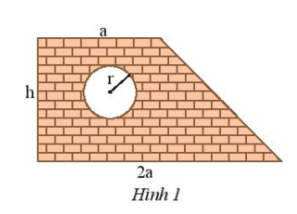
a) Diện tích bức tường là:

$\frac{1}{2}.h.(a+2a)- \pi .r^2=\frac{3}{2}.h.a- \pi.r^2$

b) Với a =  2 m ; h = 3m và r = 0,5 m 

$S = \frac{3}{2}.3.2-3,14.0,5^2 = 8,215(m^2)$

2. ĐƠN THỨC THU GỌN

Hoạt động 2 trang 8 sgk Toán 8 tập 1 CTST

Để tính thể tích của hình hộp chữ nhật ở Hình 2, bạn An viết $V = 3xy . 2x$, còn bạn Tâm viết $V = 6x^2y$. Nêu nhận xét về kết quả của hai bạn.

Đáp án:

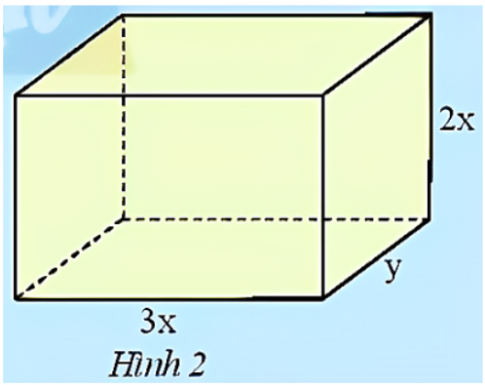
Kết quả của 2 bạn đều đúng nhưng Tâm viết gọn hơn.

Thực hành 2 trang 9 sgk Toán 8 tập 1 CTST: Thu gọn các đơn thức sau đây. Chỉ ra hệ số và bậc của chúng

$12xy^2x$

$-y(2x)y$

$x^3yx$

$5x^2y^3z^4y$

Đáp án:

3. CỘNG TRỪ ĐƠN THỨC ĐỒNG DẠNG

Hoạt động 3 trang 8 sgk Toán 8 tập 1 CTST

Cho hai hình chữ nhật A và B có các kích thước như hình.

a) Tính tổng thể tích của hình hộp chữ nhật A và B.

b) Viết biểu thức biểu diễn sự chênh lệch thể tích của A và B.

Đáp án:

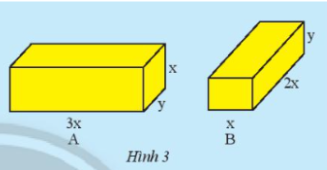
a)  $VA + VB = y.3x.x + 2x.x.y = 3x^2y + 2x^2y = 5x^2y$

b) $VA - VB = y.3x.x - 2x.x.y = 3x^2y - 2x^y = x^2y$

Thực hành 3 trang 10 sgk Toán 8 tập 1 CTST: Mỗi cặp đơn thức sau có đồng dạng không? Nếu có, hãy tìm tổng và hiệu của chúng.

$xy$ và $-6xy$

$2xy$ và $xy^2$

$-4yzx^2$ và $4x^2yz$

Đáp án:

a) Hai đơn thức đồng dạng;

$xy – (–6xy) = 7xy$; 

$xy + (–6xy) = −5xy$; 

b) Hai đơn thức không đồng dạng.

c) Hai đơn thức đồng dạng.

$(-4yzx^2)– 4x^2yz = -8x^2yz$ ; 

($-4yzx^2) + 4x^2yz = 0$

4. ĐA THỨC THU GỌN

Hoạt động 4 trang 10 sgk Toán 8 tập 1 CTST

Cho hai đa thức

A = $5x^2 - 4xy + 2x - 4x^2 + xy$;

B = $x^2 - 3xy + 2x$

Đáp án:

Với $x = -2; y = -\frac{1}{3}$

A = $5.(-2)^2 – 4 .(-2).\frac{1}{3}  + 2.(-2) – 4.(-2)^2 + (-2). \frac{1}{3} = 2$

B =  $(-2)^2 -  3 .(-2).\frac{1}{3} +2.(-2) = 2$

A = B

Thực hành 4 trang 10 sgk Toán 8 tập 1 CTST 

Thu gọn và tìm bậc của mỗi đa thức sau:

A = $x - 2y + xy - 3x + y^2$

B = $xyz - x^2y + xz - \frac{1}{2}xyz + \frac{1}{2}xz$

Đáp án:

a) $A  = y^2 – 2x – 2y + xy$;       A có bậc 2

b) $B = – x^2y - \frac{1}{2}xyz + \frac{3}{2}xz$;   B có bậc 3

Thực hành 5 trang 10 sgk Toán 8 tập 1 CTST 

Tính giá trị của đa thức.

$A = 3x^2y - 5xy - 2x^2y - 3xy$ tại $x = 3$; $y = -\frac{1}{2}$

Đáp án:

$A = x^2y – 8xy$

Với  $x = 3$ và $y = -\frac{1}{2} ta có : $A = 3^2. -\frac{1}{2} - 8.3. -\frac{1}{2} = \frac{15}{2}$

Vận dụng 2 trang 11 sgk Toán 8 tập 1 CTST: Cho hình hộp chữ nhật có các kích thước như Hình 4 (tính theo cm)

a) Viết các biểu thức tính thể tích và diện tích xung quanh của hình hộp chữ nhật đó.

b) Tính giá trị của các đại lượng trên khi a = 2 cm; h = 5 cm.

Đáp án:

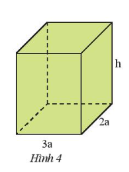
Thể tích của hình hộp chữ nhật: $3a. 2a.h = 6a^2h (cm^3)$

Diện tích xung quanh của hình hộp chữ nhật là: $2h(3a+2a) = 10ah (cm^2)$

Thay a = 2, h = 5 vào hai biểu thức ở câu a) ta có:

Thể tích của hình hộp chữ nhật: $6. 2^2 . 5 = 120 (cm^3)$

Diện tích xung quanh của hình hộp chữ nhật là: 

$10 . 2 . 5 =100 (cm^2)$

BÀI TẬP CUỐI SGK

Bài 1. Trang 11 trang 11 sgk Toán 8 tập 1 CTST

Chỉ ra các đơn thức, đa thức trong các biểu thức sau:

$-3; 2z; \frac{1}{3}xy + 1; -10x^2yz; \frac{4}{xy}; 5x - \frac{z}{2}; 1 + \frac{1}{4}$

Đáp án:

 Đơn thức: $ -3; 2z ; -10x^2yz$

 Đa thức: $\frac{1}{3}xy + 1; 5x - \frac{z}{2}$.

Bài 2. Trang 11 trang 11 sgk Toán 8 tập 1 CTST

Thu gọn các đơn thức sau. Chỉ ra hệ số, phần biến và bậc của mỗi đơn thức.

$5xyz; -xyz\frac{2}{3}y; -2x^2(-\frac{1}{6})x$

Đáp án:

Bài 3. Trang 11 trang 11 sgk Toán 8 tập 1 CTST

Thu gọn và tìm bậc của mỗi đa thức sau:

$M = x - 3 - 4y + 2x - y$

$N = -x^2t + 13t^3 + xt^2 + 5t^3 - 4$

Đáp án:

a) $M =  3x – 5y – 3$  ;  M có bậc 1

b) $N = 18t^3 + xt^2 – x^2t + xt^2 – 4$ ;  N có bậc 3

Bài 4. Trang 11 trang 11 sgk Toán 8 tập 1 CTST

Tính giá trị của đa thức $P = 3xy^2 - 6xy + 8xz + xy^2 -10xz$ tại $x = -3$; $y = -\frac{1}{2}; z = 3$.

Đáp án:

$P = 3xy^2 - 6xy + 8xz + xy^2 -10xz = 4xy^2 – 2xz - 6xy$

Với $x = -3; y = -\frac{1}{2}; z = 3$, ta có:

$P = 4.(-3).(-\frac{1}{2})^2 - 6.(-3).(-\frac{1}{2}) - 2.(-3).3 = 6$

Bài 5. Trang 11 sgk Toán 8 tập 1 CTST

Viết biểu thức biểu thị thể tích V và diện tích xung quanh S của hình hộp chữ nhật trong Hình 5. Tính giá trị của V, S khi x = 4 cm, y = 2 cm và z = 1 cm

Đáp án:

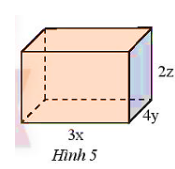
$S_{xq} = (3x + 4y).2.2z = 12xz +16yz (cm^2)$ 

$V = 4y.3x.2z = 24xyz (cm^3)$

Với  x = 4 cm; y = 2cm; z = 1 cm, ta có:

$S_{xq}= 80 (cm^2)   ; V = 192 (cm^3)$