CHƯƠNG 1. BIỂU THỨC ĐẠI SỐ 

BÀI 1. ĐƠN THỨC VÀ ĐA THỨC NHIỀU BIẾN

1. ĐƠN THỨC VÀ ĐA THỨC

HĐKP1:

a) - Các biểu thức ở nhóm A chỉ chứa các phép tính nhân và luỹ thừa đối với biến.

- Các biểu thức ở nhóm B và nhóm C chứa các phép tính khác (cộng, trừ, chia, khai căn). 

b) Các biểu thức ở nhóm A và nhóm B không chứa các phép tính nào khác ngoài các phép tính cộng, trừ, nhân và luỹ thừa (đối với biến).

=> Kết luận:

Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.

Đa thức là một tổng của những đơn thức. Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.

Chú ý:

a) Mỗi đơn thức cũng được coi là một đa thức (chỉ chứa một hạng tử)

b) Số 0 được gọi là đơn thức không, cũng gọi là đa thức không.

Ví dụ 1: (SGK – tr7)

Chú ý: Các biểu thức $\sqrt{x}, \frac{x}{y}$ không phải là đơn thức cũng không phải là đa thức, y vì biểu thức đầu chứa phép toán lấy căn bậc hai số học của biến x, biểu thức sau chứa phép toán chia giữa hai biến x và y.

Ví dụ 2: (SGK – tr7)

Thực hành 1:

a) Các đơn thức là: $\frac{4\pi r^{3}}{3}; \frac{p}{2\pi}; 0; \frac{1}{\sqrt{2}}$

b) Các đơn thức ở trên là những đa thức có một hạng tử.

Đa thức $ab - r^{2}$ có hai hạng tử.

Đa thức $x^{3}-x + 1$ có ba hạng tử.

Biểu thức $x - \frac{1}{y}$ không phải là đa thức.

Vận dụng 1:

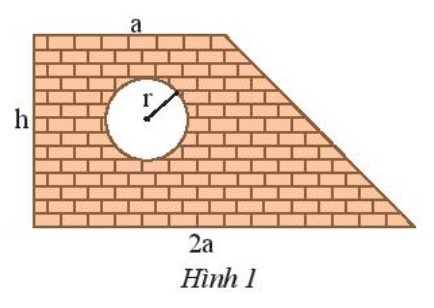
a) Biểu thức biểu thị diện tích bức tường là:

$S = \frac{1}{2}(a+2a).h -\pi.r^{2}$

$= \frac{3}{2}ah -\pi.r^{2} (m^{2})$

b) Thay a = 2 ; h = 3 và r = 0,5 vào S ta được:

$S = \frac{3}{2}. 2 . 3 -\pi.0,5^{2} = 8,215 (m^{2})$

2. ĐƠN THỨC THU GỌN

HĐKP2.

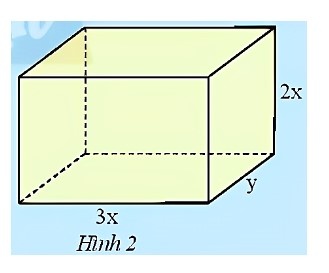
Hai kết quả đều đúng. Tuy nhiên kết quả của Tâm được viết gọn hơn (ít thừa số hơn, 3 thừa số thay vì 5 thừa số)

Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến hiện một lần dưới dạng nâng lên luỹ thừa với mũi nguyên dương.

Chú ý:

a) Tổng số mũ của tất cả các biến có trong đơn thức (có hệ số khác 0) gọi là bậc của đơn thức đó. 

b) Ta coi một số khác 0 là đơn thức thu gọn, có hệ số bằng chính số đó và có bậc bằng 0.

c) Đơn thức không (số 0) không có bậc. d) Khi viết đơn thức thu gọn ta thường viết hệ số trước, phần biến sau và các biến được viết theo thứ tự bảng chữ cái.

Ví dụ 3: SGK – tr8

Chú ý:

a) Để thu gọn một đơn thức, ta nhóm các thừa số là các số rồi tính tích của chúng nhóm các thừa số cùng một biến rồi viết tích của chúng thành luỹ thừa của biến đỏ b) Tử nay, khi nói đến đơn thức, nếu không nói gì thêm, ta hiểu đó là đơn thức thu gọn.

Thực hành 2. 

a) $12xyx = 12x^{2}y$

+ Có hệ số là 12

 + Bậc là 4.

b) $-y(2z)y = -2y^{2}z$

+ Có hệ số là -2

+ Bậc là 3

c) $x^{3}yx = x^{4}y$

+ x4y hệ số là 1; 

+ Bậc là 5

d) $5x^{2}y^{3}z^{4}.y = 5x^{2}y^{4}z^{4}$

+ Hệ số: 5

+ Bậc là 10

3. CỘNG, TRỪ ĐƠN THỨC ĐỒNG DẠNG

HĐKP3.

a) 3x.y.x + x.2x.y = 3x2y + 2x2y = (3+2)x2y = 5x2y

b) 3x.y.x – x.2x.y = 3x2y – 2x2y = (3-2).x2.y = x2y

=> Kết luận:

Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.

Để cộng, trừ (hay tìm tổng, hiệu) hai đơn thức đồng dạng, ta cộng, từ hệ số của chúng và giữ nguyên phần biến.

Ví dụ 4: SGK – tr9

Thực hành 3: 

a) xy và -6xy là hai đơn thức đồng dạng;

• xy + (–6xy) = −5xy; 

• xy – (–6xy) = 7xy; 

b) 2xy và $xy^{2}$ là hai đơn thức không đồng dạng.

c) $-4yzx^{2}$ và $4x^{2}yz$ là hai đơn thức đồng dạng.

• $-4yzx^{2} + 4x^{2}yz= 0$

• $-4yzx^{2}-4x^{2}yz=-8x^{2}yz$

4. ĐA THỨC THU GỌN

HĐKP4.

Giá trị của A tại x = -2; y = 13 là:

$5.(-2)^{2}-4 .(-2).\frac{1}{3}+2.(-2) -4.(-2)^{2} + (-2).\frac{1}{3} = 20 + \frac{8}{3}-4 -16-\frac{2}{3}=2$

Giá trị của B tại x = -2; $y = \frac{1}{3}$ là $(-2)^{2}-3 .(-2).\frac{1}{3}+2.(-2) =  4 + 2 -4 = 2$

Vậy giá trị của hai đa thức tại x =  -2 ; $y = \frac{1}{3}$ bằng nhau

=> Kết luận:

Đa thức thu gọn là đa thức không chứa hhai hạng tử nào đồng dạng.

Chú ý:

a) Biến đổi một đa thức thành đa thức thu gọn gọi là thu gọn đa thức đỏ. 

b) Để thu gọn một đa thức, ta nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng đó với nhau.

c) Bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức gọi là bậc của đa thức đó.

Ví dụ 5: SGK – tr 10

Thực hành 4: 

a) $A  =  x -2y + xy -  3x + y^{2}$

= $y^{2} + xy-2x-2y$

⇒ bậc của A là 2.

b) $B = xyz- x^{2}y + xz - \frac{1}{2}xyz + \frac{1}{2}xz$

$B = -\frac{1}{2}xyz-x^{2}y + \frac{3}{2}xz$

bậc của B là 3.

Thực hành 5.

$A = 3x^{2}y-5xy - 2x^{2}y-3xy$

$= (3x^{2}y - 2x^{2}y) +(-5xy-3xy)$

$= x^{2}y-8xy$

Thay x = 3 và $y = -\frac{1}{2}$ vào A ta được:

$A = 3^{2}.(-\frac{1}{2}-8.3.(-\frac{1}{2}) = \frac{15}{2}$

Vận dụng 2.

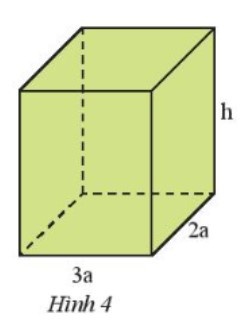
a) Biểu thức tính thể tích của hình hộp chữ nhật:

$V = 6a^{2}h$

Biểu thức tính diện tích xung quanh:

S = 10ah

b) Khi a = 2 cm; h = 5 cm thì:

$V = 6.2^{2}.5 = 120 cm^{3}$; 

$S = 10.2.5 =100 cm^{2}$