Đáp án toán 8 chân trời bài Bài tập cuối chương 3
Đáp án bài Bài tập cuối chương 3. Bài giải được trình bày ngắn gọn, chính xác giúp các em học Toán 8 Chân trời sáng tạo dễ dàng. Từ đó, hiểu bài và vận dụng vào các bài tập khác. Đáp án chuẩn chỉnh, rõ ý, dễ tiếp thu. Kéo xuống dưới để xem chi tiết
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI TẬP CUỐI CHƯƠNG 3
BÀI TẬP TỰ LUẬN
Bài tập 8: Cho hình bình hành ABCD. Các điểm E, F thuộc đường chéo AC sao cho AE=EF=FC. Gọi M là giao điểm của BF và CD, N là giao điểm của DE và AB. Chứng minh rằng:
a) M, N theo thứ tự là trung điểm của CD, AB;
b) EMFN là hình bình hành.
Đáp án chuẩn:
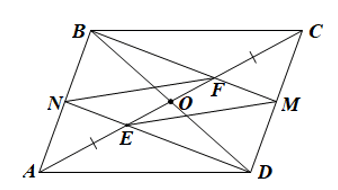
a) BF hay BM là đường trung tuyến của ![]() BCD.
BCD.
![]() M là trung điểm của CD.
M là trung điểm của CD.
CMTT:
DE hay DN cũng là đường trung tuyến của ![]() ABD.
ABD.
![]() N là trung điểm của AB.
N là trung điểm của AB.
b) 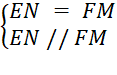
![]() EMFN là hình bình hành.
EMFN là hình bình hành.
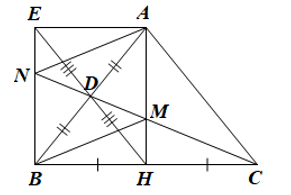
Bài tập 9: Cho tam giác ABC cân tại A. Gọi H, D lần lượt là trung điểm của các cạnh BC và AB.
a) Chứng minh rằng tứ giác ADHC là hình thang.
b) Gọi E là điểm đối xứng với H qua D. Chứng minh rằng tứ giác AHBE là hình chữ nhật.
c) Tia CD cắt AH tại M và cắt BE tại N. Chứng minh rằng tứ giác AMBN là hình bình hành.
Đáp án chuẩn:
a) DH // AC
![]() ADHC là hình thang.
ADHC là hình thang.
b) AHBE là hình bình hành.
Mà ![]()
![]() AHBE là hình chữ nhật.
AHBE là hình chữ nhật.
c) D là trung điểm của AB
D là trung điểm của NM
AB cắt NM tại D
![]() AMBN là hình bình hành.
AMBN là hình bình hành.
Bài tập 10: Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của AB, AC, BC.
a) Chứng minh rằng tứ giác ANEB là hình thang vuông.
b) Chứng minh rằng tứ giác ANEM là hình chữ nhật.
c) Qua M kẻ đường thẳng song song với BN cắt tia EN tại F. Chứng minh rằng tứ giác AFCE là hình thoi.
d) Gọi D là điểm đối xứng của E qua M. Chứng minh rằng A là trung điểm của DF.
Đáp án chuẩn:
a) ANEB có: 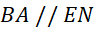
![]() ANEB là hình thang
ANEB là hình thang
Mà 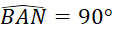
![]() ANEB là hình thang vuông.
ANEB là hình thang vuông.
b) 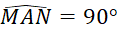 ;
; 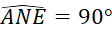 ;
; 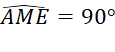
![]() ANEM là hình chữ nhật.
ANEM là hình chữ nhật.
c) AFCE là hình bình hành.
mà 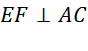
![]() AFCE là hình thoi.
AFCE là hình thoi.
d) ![]() AF // CE và AF = CE (tính chất hình thoi)
AF // CE và AF = CE (tính chất hình thoi)
CMTT câu c, ta cũng có ADBE là hình thoi
![]()
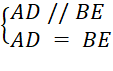
+ Ta có 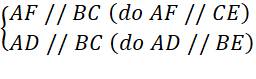
theo tiên đề Euclid ta có: AD và AF trùng nhau hay ba điểm F, A, D thẳng hàng (1)
+ Ta có 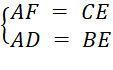
Mà CE = BE (do E là trung điểm của BC)
![]() AF = AD (2)
AF = AD (2)
Từ (1) và (2) ta có A là trung điểm của DF.
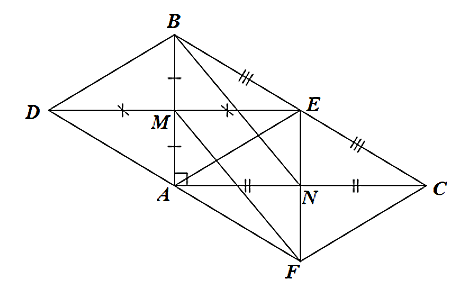
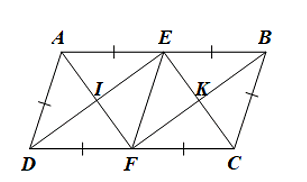
Bài tập 11: Cho hình bình hành ABCD có AB = 2AD. Gọi E và F lần lượt là trung điểm của AB và CD, I là giao điểm của AF và DE, K là giao điểm của BF và CE.
a) Chứng minh rằng tú giác AECF là hình bình hành. tạo
b) Tứ giác AEFD là hình gì? Vì sao?
c) Chứng minh rằng tứ giác EIFK là hình chữ nhật.
d) Tìm điều kiện của hình bình hành ABCD để tứ giác EIFK là hình vuông.
Đáp án chuẩn:
a) 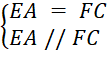
![]() AECF là hình bình hành.
AECF là hình bình hành.
b) AEFD là hình thoi.
c) 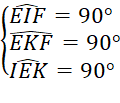
![]() EIFK là hình chữ nhật.
EIFK là hình chữ nhật.
d) Tứ giác EIFK là hình vuông thì hình bình hành ABCD phải là hình chữ nhật.
Bài tập 12: Cho hình bình hành ABCD có AD = 2AB. Từ C vẽ CE vuông góc với AB tại E. Nối E với trung điểm M của AD. Từ M vẽ MF vuông góc với CE tại F, MF cắt BC tại N.
a) Tứ giác MNCD là hình gì?
b) Chứng minh tam giác EMC cân tại M.
c) Chứng minh rằng ![]()
Đáp án chuẩn:
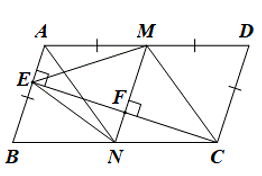
a) Hình bình hành MNCD có MD = CD nên MNCD là hình thoi.
b) ME = MC
![]()
![]() EMC cân tại M.
EMC cân tại M.
c) 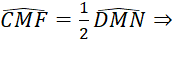
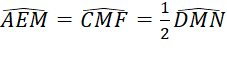
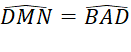
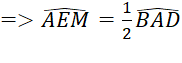
hay 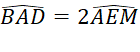
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây

Bình luận