Đáp án toán 8 chân trời bài 2 Các trường hơp đồng dạng của hai tam giác
Đáp án bài 2 Các trường hơp đồng dạng của hai tam giác. Bài giải được trình bày ngắn gọn, chính xác giúp các em học Toán 8 Chân trời sáng tạo dễ dàng. Từ đó, hiểu bài và vận dụng vào các bài tập khác. Đáp án chuẩn chỉnh, rõ ý, dễ tiếp thu. Kéo xuống dưới để xem chi tiết
BÀI 2. CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA HAI TAM GIÁC
1. TRƯỜNG HỢP ĐỒNG DẠNG THỨ NHẤT (C.C.C)
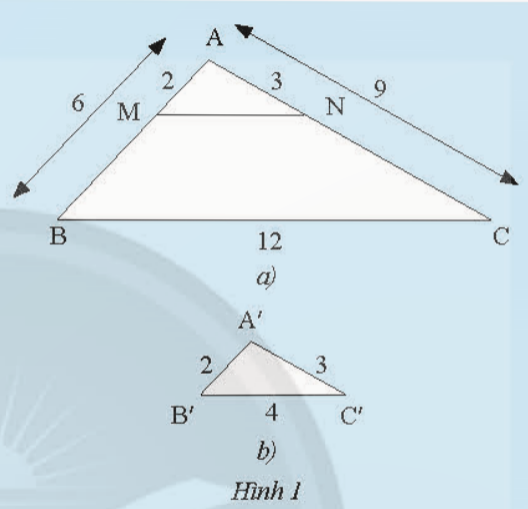
Bài 1: Cho tam giác ABC và tam giác A'B'C' có các kích thước như Hình 1. Trên cạnh AB và AC của tam giác ABC lần lượt lấy hai điểm M, N sao cho AM = 2 cm, AN = 3 cm
a) So sánh các tỉ số ![]()
b) Tính độ dài đoạn thẳng MN
c) Em có nhận xét gì về mối quan hệ giữa các tam giác ABC, AMN và A'B'C'
Đáp án chuẩn:
a) ![]()
b) MN = 4
c) ΔAMN=ΔA′B′C′, ΔA′B′C′ ᔕ ΔABC và ΔAMN ᔕ ΔABC
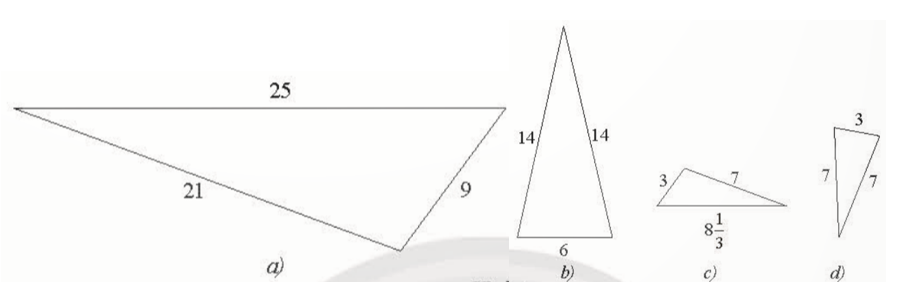
Bài 2: Tìm trong Hình 4 các cặp tam giác đồng dạng
Đáp án chuẩn:
Hình b) và d)
Hình a) và c)
2. TRƯỜNG HỢP ĐỒNG DẠNG THỨ HAI (C.G.C)
Bài 1: Cho tam giác DEF và ABC có DE= ![]() AB,DF=
AB,DF= ![]() AC,
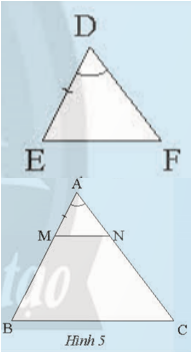
AC, ![]() (Hình 5). Trên tia AB, lấy điểm M sao cho AM = DE. Qua M kẻ MN // BC (N∈AC)
(Hình 5). Trên tia AB, lấy điểm M sao cho AM = DE. Qua M kẻ MN // BC (N∈AC)
a) So sánh các tỉ số ![]()
b) So sánh AN và DF
c) Tam giác AMN có đồng dạng với tam giác ABC không?
d) Dự đoán sự đồng dạng của hai tam giác DEF và ABC
Đáp án chuẩn:
a) ![]()
b) AN = DF
c) ΔAMN ᔕ ΔABC
d) ΔDEF ᔕ ΔABC
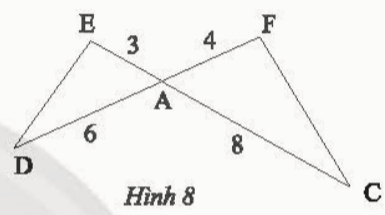
Bài 2: Cho tam giác ADE và tam giác ACF có các kích thước như trong Hình 8. Chứng minh rằng ΔADE ᔕ ΔACF
Đáp án chuẩn:
![]()
![]() (hai góc đối đỉnh)
(hai góc đối đỉnh)
=> ΔADE ᔕ ΔACF (c.g.c)
3. TRƯỜNG HỢP ĐỒNG DẠNG THỨ BA (G.G)
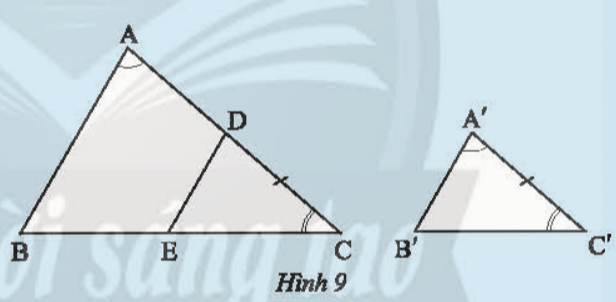
Bài 1: Cho hai tam giác ABC và A’B’C’ có ![]() ;
; ![]() (Hình 9).Trên cạnh AC, Lấy điểm D sao cho DC = A'C'. Qua D kẻ đường thẳng song song với AB cắt cạnh BC tại E.
(Hình 9).Trên cạnh AC, Lấy điểm D sao cho DC = A'C'. Qua D kẻ đường thẳng song song với AB cắt cạnh BC tại E.
a) Tam giác DEC có đồng dạng với tam giác ABC không?
b) Nhận xét về mối quan hệ giữa tam giác A'B'C' và tam giác DEC
c) Dự đoán về sự đồng dạng của hai tam giác A'B'C' và ABC
Đáp án chuẩn:
a) DE // AB => ΔDEC ᔕ ΔABC
b) ![]() (cùng =
(cùng = ![]()
A'C' = DC (gt)
![]() (gt)
(gt)
=> ΔA′B′C′=ΔDEC (g.c.g)
c) ΔA′B′C′ᔕΔABC
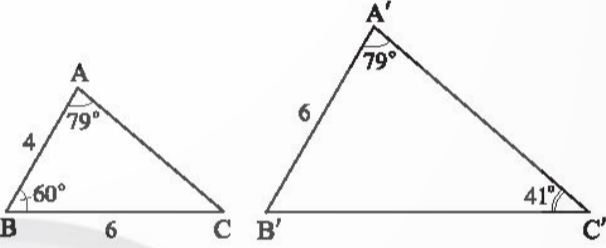
Bài 2: Quan sát Hình 12.
a) Chứng minh rằng ΔABC ᔕ ΔA′B′C′
b) Tính độ dài B'C'
Đáp án chuẩn:
a) ![]()
![]()
=> ΔABCᔕΔA′B′C′ (g.g)
b) B'C' = 9
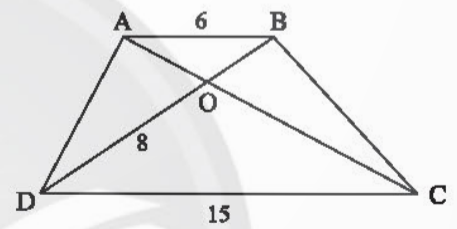
Bài 3: Cho hình thang ABCD (AB // CD) có AB = 6m, CD = 15m, OD = 8m (Hình 13). Tính độ dài đoạn thẳng OB
Đáp án chuẩn:
OB = ![]()
Bài 4: Qua các trường hợp đồng dạng của hai tam giác, hãy trả lời câu hỏi ở Hoạt động khởi động (trang 67)
Đáp án chuẩn:
Trường hợp | Hai tam giác bằng nhau | Hai tam giác đồng dạng |
1 | 3 cạnh tương ứng bằng nhau | 3 cạnh tương ứng tỉ lệ |
2 | 2 cạnh tương ứng và một góc kề với hai cạnh bằng nhau | 2 cạnh tương ứng tỉ lệ |
3 | 1 cạnh và 2 góc kề tương ứng bằng nhau | Chỉ 2 góc bằng nhau, không cần có điều kiện cạnh |
BÀI TẬP CUỐI SGK
Bài 1:
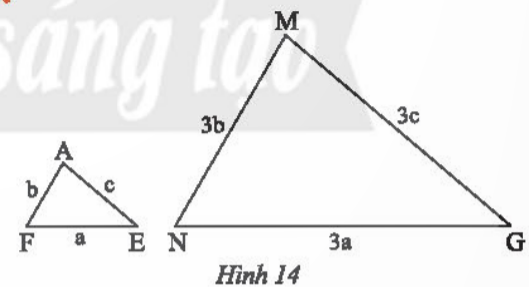
a) Tam giác AFE và MNG ở Hình 14 có đồng dạng với nhau không? Vì sao?
b) Biết tam giác AFE có chu vi bằng 15 cm. Tính chu vi tam giác MNG
Đáp án chuẩn:
a) ![]() =
= ![]()
![]()
=> ΔAFE ᔕ ΔMNG
b) Chu vi MNG = 15 . 3 = 45 (cm)
Bài 2: Tam giác ABC có độ dài AB = 4 cm, AC = 6 cm, BC = 9 cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có chu vi bằng 66,5 cm. Hãy tính độ dài các cạnh của tam giác A'B'C'
Đáp án chuẩn:
A′B′ = 14, A′C′ = 21, B′C′ = ![]()
Bài 3: Một công viên có hai đường chạy bộ hình tam giác đồng dạng như Hình 15. Kích thước của con đường bên trong lần lượt là 300 m, 350 m và 550 m. Cạnh ngắn nhất của con đường bên ngoài là 660 m. Nam chạy bốn vòng trên con đường bên trong, Hùng chạy hai vòng trên con đường bên ngoài. So sánh quãng đường chạy được của hai bạn.
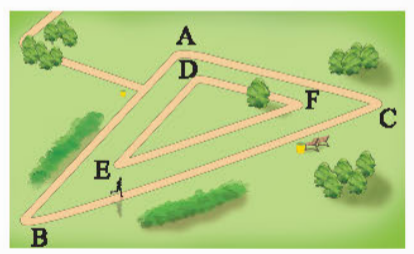
Đáp án chuẩn:
Bằng nhau
Bài 4: Xét xem cặp tam giác nào trong các Hình 16a, 16b đồng dạng?
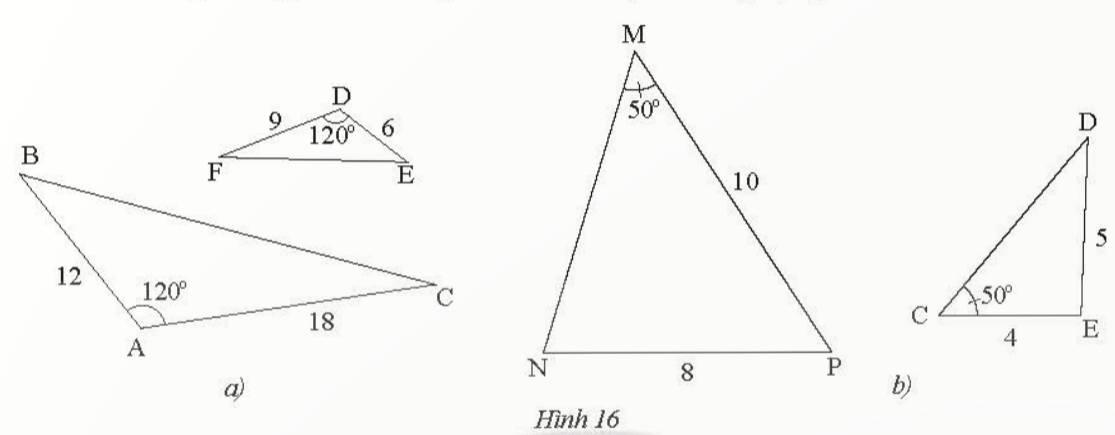
Đáp án chuẩn:
a) ΔDEF ᔕ ΔABC (c.g.c)
b) Hai tam giác này không đồng dạng
Bài 5: Trong Hình 17, cho biết DE = 6 cm, EF= 7,8 cm, NP = 13 cm, NM = 10 cm, ![]() và
và ![]() = 420. Tính
= 420. Tính ![]()
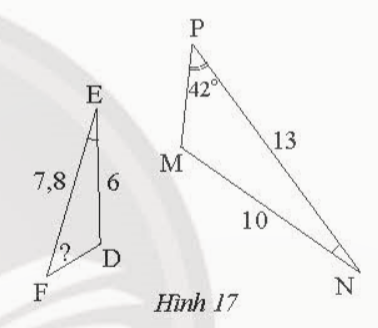
Đáp án chuẩn:
![]() = 420
= 420
BÀI 2. CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA HAI TAM GIÁC
Bài 6: a) Cho tam giác ABC có AB = 12 cm, AC = 15 cm, BC = 18 cm. Trên cạnh AB, lấy điểm E sao cho AE = 10 cm. Trên cạnh AC, lấy điểm F sao cho AF = 8 cm (Hình 18a). Tính độ dài đoạn thẳng EF
b) Trong Hình 18b, cho biết FD = FC, BC = 9 dm, DE = 12 dm, AC = 15 dm, MD = 20 dm. Chứng minh rằng ΔABCᔕΔMED
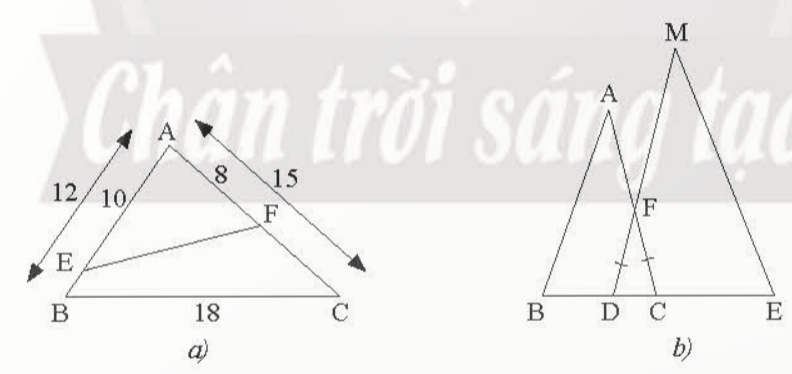
Đáp án chuẩn:
a) EF = 12 cm
b) ![]() =
= 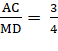
![]()
=> ΔABC ᔕ ΔMED (c.g.c)
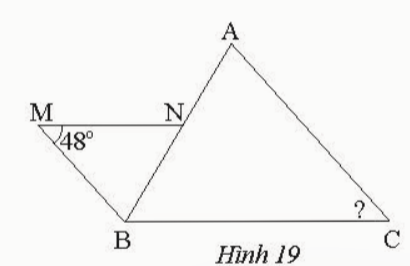
Bài 7: Trong Hình 19, cho biết MN // BC, MB // AC.
a) Chứng minh ΔBNM ᔕ ΔABC
b) Tính ![]()
Đáp án chuẩn:
a) ![]() (hai góc so le trong)
(hai góc so le trong)
![]() (hai góc so le trong)
(hai góc so le trong)
=> ΔBNM ᔕ ΔABC (g.g)
b) ![]() 480
480
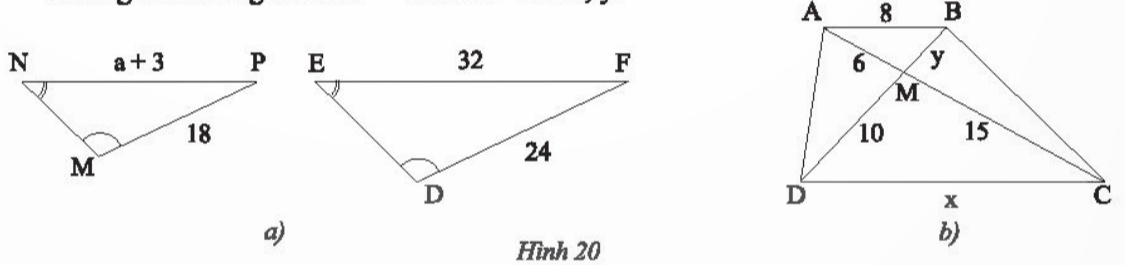
Bài 8: a) Trong Hình 20a, cho biết ![]() ;
; ![]() , MP = 18 m, DF = 24 m, EF = 32 m, NP = a + 3 (m). Tìm a.
, MP = 18 m, DF = 24 m, EF = 32 m, NP = a + 3 (m). Tìm a.
b) Cho ABCD là hình thang (AB // CD) (Hình 20b)
Chứng minh rằng ΔAMB ᔕ ΔCMD. Tìm x, y
Đáp án chuẩn:
a) a = 21
b) x = 20, y = 4
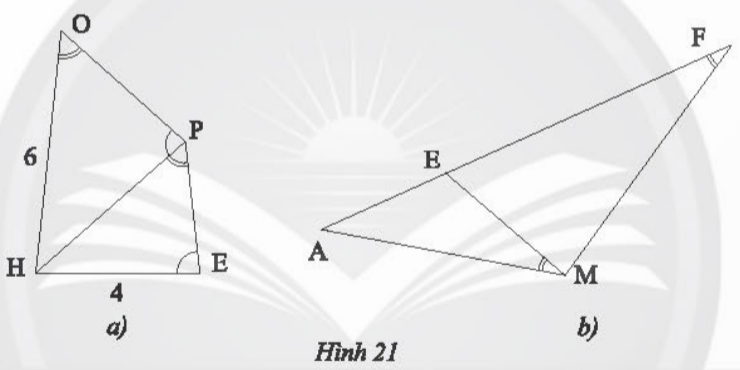
Bài 9: a) Trong Hình 21a, cho biết ![]() ;
; ![]() , OH= 6cm và HE = 4 cm. Tính độ dài đoạn thẳng HP.
, OH= 6cm và HE = 4 cm. Tính độ dài đoạn thẳng HP.
b) Trong Hình 21b, cho biết ![]() . Chứng minh rằng AM2 =AE.AF
. Chứng minh rằng AM2 =AE.AF
Đáp án chuẩn:
a) HP = 2![]()
b) ΔAEM ᔕ ΔAMF => ![]() =
= ![]() => AM2 =AE.AF
=> AM2 =AE.AF
Bài 10: Đường đi và khoảng cách từ nhà anh Thanh (điểm M) đến công ty (điểm N) được thể hiện trong Hình 22. Hãy tìm con đường ngắn nhất để đi từ nhà của anh Thanh đến công ty.
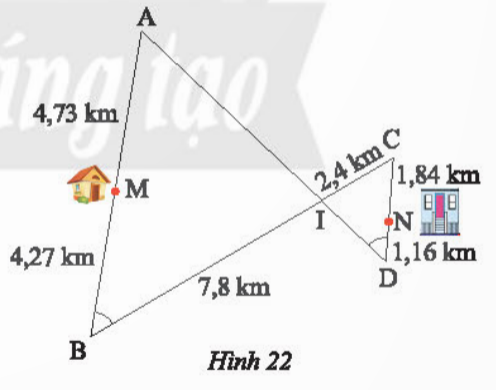
Đáp án chuẩn:
M -> A -> I -> D -> N

Bình luận