BÀI 3. CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA HAI TAM GIÁC VUÔNG

1. ÁP DỤNG CÁC TRƯỜNG HỢP ĐỒNG DẠNG CỦA TAM GIÁC VÀO TAM GIÁC VUÔNG

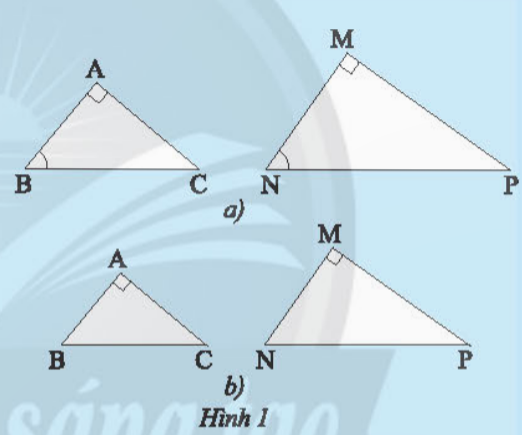
Bài 1: a) Từ trường hợp đồng dạng thứ ba của hai tam giác, xét xem tam giác ABC vuông tại A và tam giác MNP vuông tại M có thì hai tam giác đó có đồng dạng với nhau không?

b) Từ trường hợp đồng dạng thứ hai của hai tam giác, xét xem nếu tam giác ABC vuông tại A và tam giác MNP vuông tại M có thì tam giác đó có đồng dạng với nhau không.

Đáp án chuẩn:

a) ΔABC ᔕ ΔMNP (g.g)

b) ΔABC ᔕ ΔMNP (c.g.c)

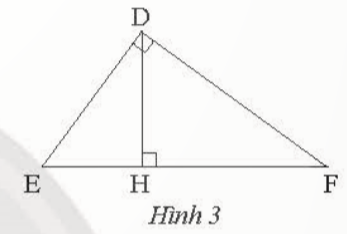
Bài 2: Cho tam giác DEF vuông tại D có DH là đường cao (Hình 3) Chứng minh rằng DE² =EH.EF

Đáp án chuẩn: 

ΔHED ᔕ ΔDEF (g.g) nên => DE² =EH.EF

Bài 3: Tính chiều cao của cột cờ trong Hoạt động khởi động (trang 73)

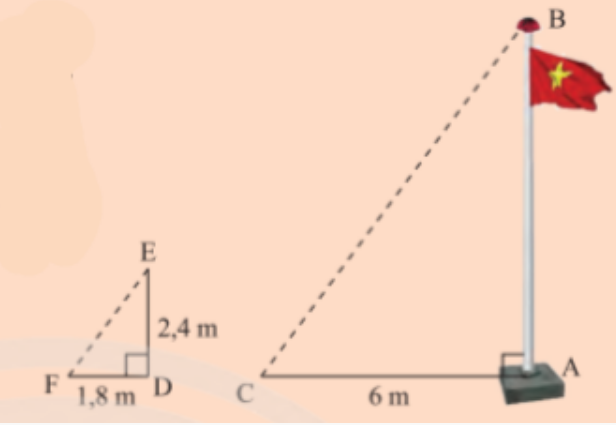
Đáp án chuẩn: 

8 m

2. THÊM MỘT DẤU HIỆU NHẬN BIẾT HAI TAM GIÁC VUÔNG ĐỒNG DẠNG

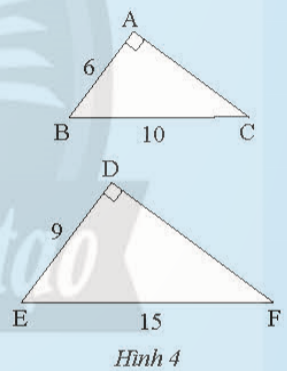
Bài 1:  Cho hai tam giác vuông ABC và DEF có các kích thước như Hình 4.

a) Hãy tính độ dài cạnh AC và DF.

b) So sánh các tỉ số

c) Dự đoán sự đồng dạng của hai tam giác ABC và DEF

Đáp án chuẩn:

a) AC = 8; DF = 12

b) =

c) ΔABC ᔕ ΔDEF

Bài 2: Trong Hình 6, tam giác nào đồng dạng với tam giác DEF?

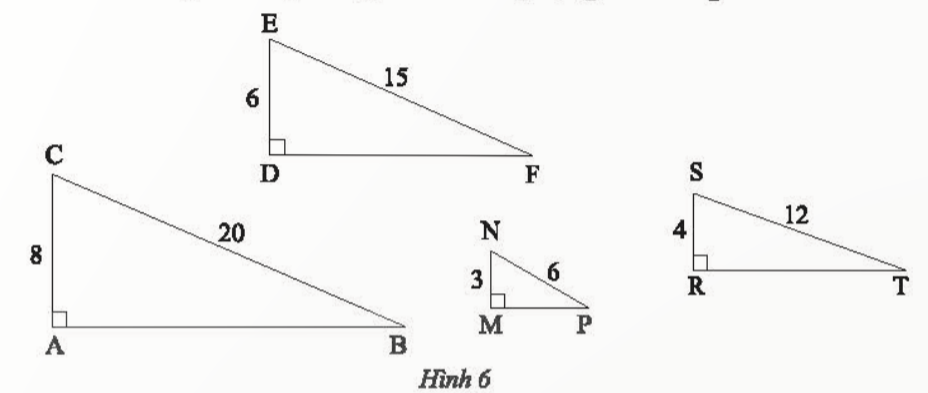
Đáp án chuẩn: 

ΔABC ᔕ ΔDFE

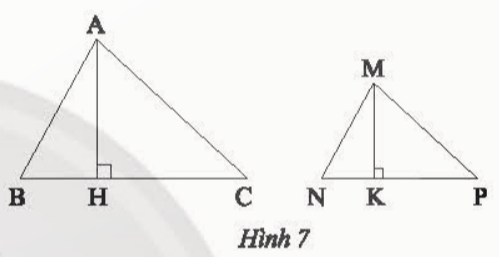
Bài 3: Trong Hình 7, biết ΔMNP ᔕ ΔABC với tỉ số đồng dạng k =, hai đường cao tương ứng là MK và AH

a) Chứng minh rằng ΔMNK ᔕ ΔABH và = k

b) Gọi S₁ là diện tích tam giác MNP và S₂ là diện tích tam giác ABC. Chứng minh rằng  = k²

Đáp án chuẩn:

a) Tam giác vuông MNK và ABH có:

=> ΔMNKᔕΔABH => = k

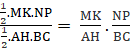b)  = k² 

BÀI TẬP CUỐI SGK

Bài 1: Hãy tìm cặp tam giác vuông đồng dạng trong Hình 8.

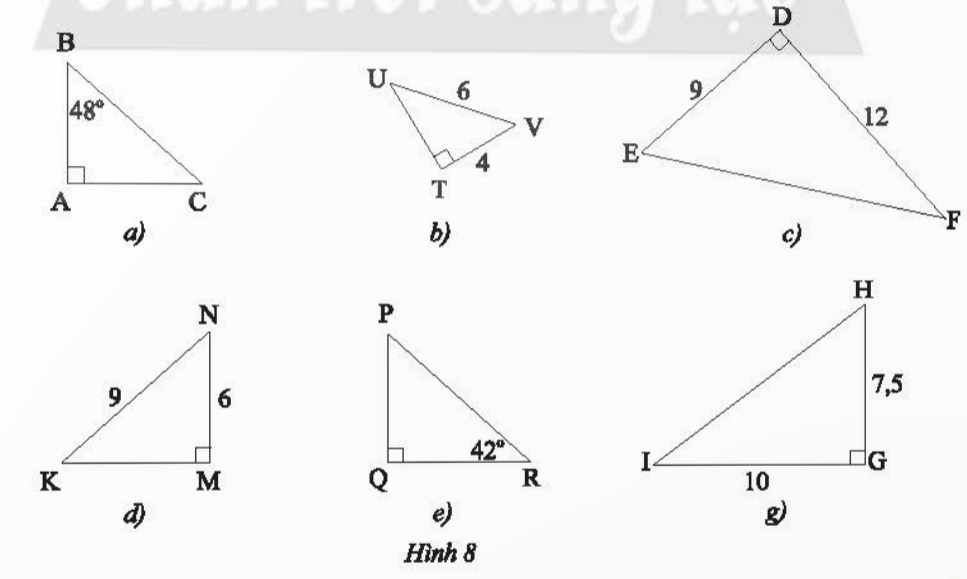
Đáp án chuẩn:

ΔTUV ᔕ ΔMKN

ΔDEF ᔕΔGHI

ΔBAC ᔕ ΔPQR 

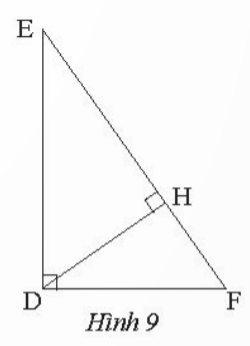
Bài 2: Quan sát hình 9

a) Chứng minh rằng ΔDEF ᔕ ΔHDF

b) Chứng minh DF² =FH.FE

c) Biết EF = 15 cm, FH = 5,4 cm. Tính độ dài đoạn thẳng DF

Đáp án chuẩn:

a) Xét tam giác vuông DEF và HDE có:  chung

=> ΔDEFᔕΔHDF (g.g)

b) ΔDEF ᔕ ΔHDF nên = => DF² = FH.FE

c) DF = 9 (cm)

Bài 3: Trong Hình 10, biết MB = 20m, MF = 2m, EF = 1,65 m. Tính chiều cao AB của ngọn tháp

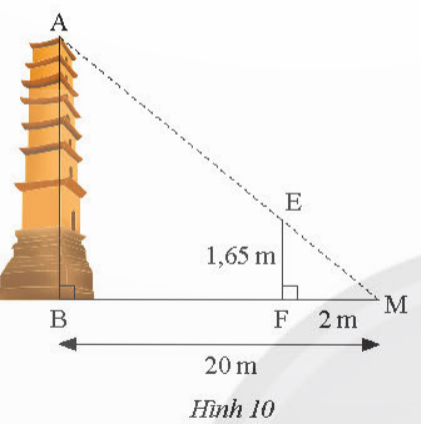
Đáp án chuẩn:

AB = 16,5 (m)

Bài 4: Trong Hình 11, cho biết , BE = 25cm, AB = 20cm, DC = 15cm. Tính độ dài đoạn thẳng CE

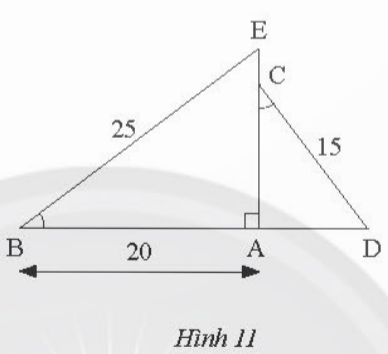
Đáp án chuẩn:

CE = 3

Bài 5: Quan sát Hình 12. Chứng minh rằng:

a) ΔABH ᔕ ΔDCB                                               b) =  

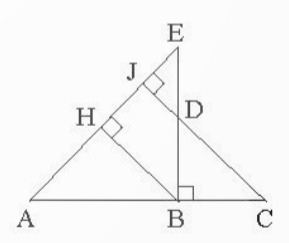
Đáp án chuẩn:

a) Xét tam giác vuông ABH và DCB ta có:  

=> ΔABH ᔕ ΔDCB (g.g) 

b) ΔDCBᔕΔAEB (g.g)

=> =  

Bài 6: Một người đo chiều cao của một tòa nhà nhờ một cọc chôn xuống đất, cọc cao 3m và đặt cách xa tòa nhà 27 m. Sau khi người ấy lùi ra xa cách cọc 1,2 m thì nhìn thấy đầu cọc và đỉnh tòa nhà cùng nằm trên một đường thẳng. Hỏi tòa nhà cao bao nhiêu mét, biết rằng khoảng cách từ chân đến mắt người ấy là 1,5m

Đáp án chuẩn:

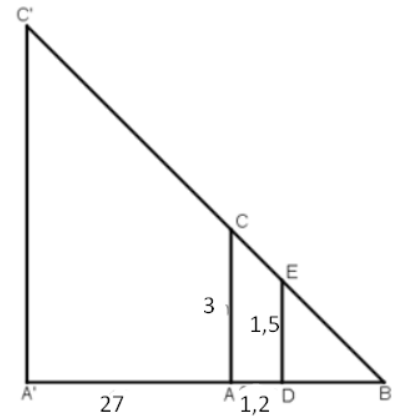
24,5m.

Bài 7: Cho tam giác ABC vuông tại A có đường cao AH. Kẻ HM vuông góc với AB tại M.

a) Chứng minh rằng ΔAMH ᔕ ΔAHB

b) Kẻ HN vuông góc với AC tại N. Chứng minh rằng AM . AB = AN . AC

c) Chứng minh rằng ΔANM ᔕ ΔABC

d) Cho biết AB = 9cm, AC = 12 cm. Tính diện tích tam giác AMN

Đáp án chuẩn:

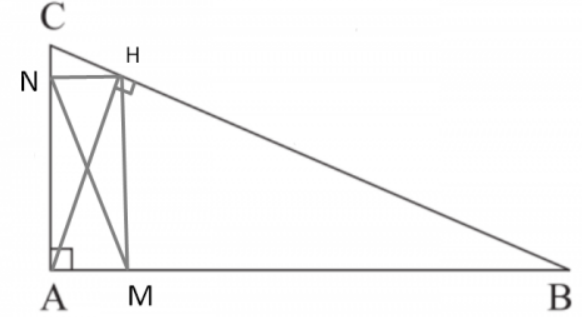
a) Xét tam giác vuông AMH và AHB ta có: chung => ΔAMH ᔕ ΔAHB (g.g)

b) AM. AB = AH²

AN.AC=AH² 

=> AM . AB = AN . AC

c) Xét tam giác vuông AMN và ABC ta có: =   => ΔANM ᔕ ΔABC (c.g.c)

d) Diện tích tam giác AMN: 12,4416(cm²)