BÀI 6. HÌNH THOI (2 tiết)

I. Định nghĩa

Hoạt động 1 trang 113 sgk Toán 8 tập 1 CD: So sánh độ dài các cạnh của tứ giác ABCD ở hình 56. 

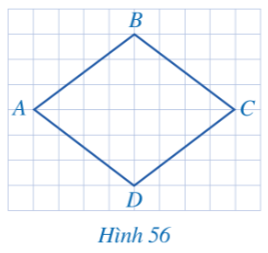
Giải nhanh:

bằng nhau.

II. Tính chất

Hoạt động 2 trang 113 sgk Toán 8 tập 1 CD: Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O (Hình 58).

a) Hình thoi ABCD có là hình bình hành hay không?

b) Hai đường chéo AC và BD có vuông góc với nhau hay không?

c) Hai tam giác ABC và ADC có bằng nhau hay không? Tia AC có phải là tia phân giác của BAD hay không?

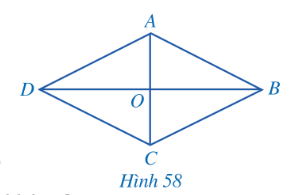
Giải nhanh:

a) Do là hình thoi => Tứ giác là hình bình hành.

b) Do là hình bình hành nên

Xét và có: chung; ;

=> (c.c.c) => . Mà

=> hay tại .

c) Xét và có: chung; (theo câu a)

=> (c.c.c) => nên là phân giác

Luyện tập 1 trang 114 sgk Toán 8 tập 1 CD: Cho hình thoi ABCD có . Chứng minh tam giác ABD là tam giác đều.

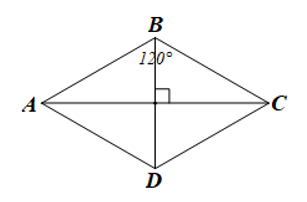
Giải nhanh:

là hình thoi, ;  . => cân tại .

Lại có là phân giác =>

Vậy là tam giác cân có một góc nên là tam giác đều.

III. Dấu hiệu nhận biết

Hoạt động 3 trang 114 sgk Toán 8 tập 1 CD:

a) Cho hình bình hành ABCD có hai cạnh kề AB và BC bằng nhau. ABCD có phải là hình thoi hay không?

b) Cho hình bình hành ABCD có hai đường chéo AC và BD vuông góc với nhau (Hình 60).

• Đường thẳng AC có phải là đường trung trực của đoạn thẳng BD hay không?
• ABCD có phải là hình thoi hay không?

Giải nhanh:

a) Do là hình bình hành nên và .

Mà => => là hình thoi.

b) Do là hình bình hành => Hai đường chéo và cắt nhau tại trung điểm mỗi đường.=> tại trung điểm của => là trung trực của .

Vì là đường trục trực của =>

=> hình bình hành có hai cạnh kề và bằng nhau nên là hình thoi.

Luyện tập 2 trang 115 sgk Toán 8 tập 1 CD: Cho tam giác ABC cân tại A có M là trung điểm BC. Trên tia đối của tia MA lấy điểm N sao cho MN = MA. Chứng minh tứ giác ABNC là hình thoi.

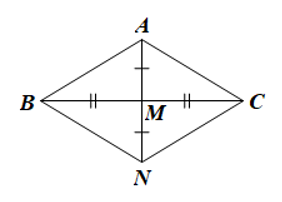
Giải nhanh:

Tứ giác có hai đường chéo và cắt nhau tại trung điểm mỗi đường.

=> là hình bình hành.

Mặt khác cân tại , là trung tuyến, cũng là đường cao => hay => Hình bình hành là hình thoi

IV. Bài tập

Bài 1 trang 115 sgk Toán 8 tập 1 CD: Cho hình bình hành ABCD có tia AC là tia phân giác của góc DAB. Chứng minh ABCD là hình thoi.

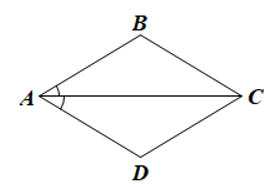
Giải nhanh:

Do là phân giác của =>

Do là hình bình hành => => . Do đó

Xét có nên cân tại =>

Hình bình hành là hình thoi.

Bài 2  trang 115 sgk Toán 8 tập 1 CD: Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Chứng minh:

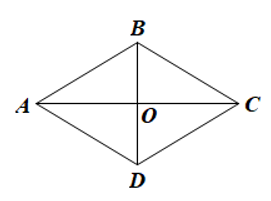
Giải nhanh:

là hình thoi => vuông góc với tại trung điểm của mỗi đường.

Do đó :

Ta có :

Xét vuông tại : =>

Bài 3 trang 115 sgk Toán 8 tập 1 CD: Cho hình thoi ABCD có . Tính số đo mỗi góc của hình thoi ABCD.

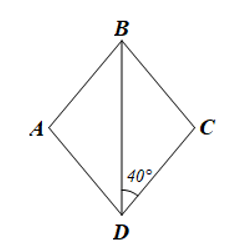
Giải nhanh:

là hình thoi nên là phân giác

Do đó =>

Do là hình thoi nên , do đó

Suy ra

Bài 4 trang 115 sgk Toán 8 tập 1 CD: Hình 62 mô tả một ô lưới mắt cáo có dạng hình thoi với độ dài của hai đường chéo là 45 mm và 90 mm. Độ dài cạnh của ô lưới mắt cáo đó là bao nhiêu milimét (làm tròn kết quả đến hàng đơn vị)?

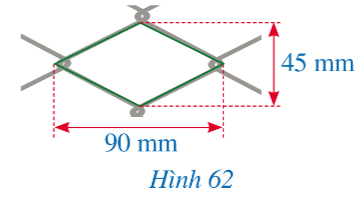
Giải nhanh:

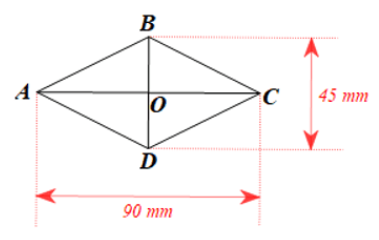
Có :

Do là hình thôi => Hai đường chéo và vuông góc tại trung điểm của mỗi đường =>

Xét vuông tại .  

Suy ra

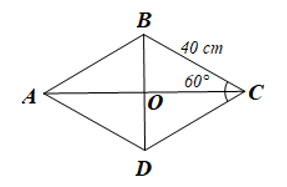
Bài 5 trang 115 sgk Toán 8 tập 1 CD: Một viên gạch trang trí có dạng hình thoi với độ dài cạnh là 40 cm và số đo một góc là 60° (Hình 63). Diện tích của viên gạch đó là bao nhiêu centimét vuông (làm tròn kết quả đến hàng phần trăm)?

Giải nhanh:

Giả sử viên gạch được mô tả bởi hình thoi như hình vẽ trên với

+) có => cân tại , mà => đều.

Do đó

+) Do là hình thoi => Đường chéo vuông góc với đường chéo tại trung điểm cả mỗi đường. =>

Xét vuông tại : =>

=> Mà là trung điểm =>

 .