BÀI 8. TRƯỜNG HỢP ĐỒNG DẠNG THỨ BA CỦA TAM GIÁC

I. TRƯỜNG HỢP ĐỒNG DẠNG THỨ BA : GÓC- GÓC

Bài 1:  Cho hai tam giác ABC và MNP thỏa mãn = 50⁰ ; = 60⁰; = 60⁰; = 70⁰.Chứng minh △ABC  ᔕ △MNP. 

Giải nhanh:

Tam giác MNP có + + = 180⁰ Mà = 60⁰; = 70⁰ => = 50⁰

Ta có : = = 50⁰ ; = = 60⁰ Suy ra △ABC  ᔕ △MNP (g.g)

II. ÁP DỤNG TRƯỜNG HỢP ĐỒNG DẠNG THỨ BA CỦA TAM GIÁC VÀO TAM GIÁC VUÔNG

Bài 1: Cho tam giác nhọn ABC có hai đường cao AD, BE cắt nhau tại H. Chứng minh HA.HD = HB.HE 

Giải nhanh:

Ta có : = = 90⁰ ; = (hai góc đối đỉnh)

Suy ra : △AEH ᔕ △BDH (g.g) Do đó: = hay HA.HD = HB.HE

BÀI TẬP CUỐI SGK

Bài 1: Cho Hình 86. a) Chứng minh △MNP ᔕ △ABC.                      b) Tìm x.

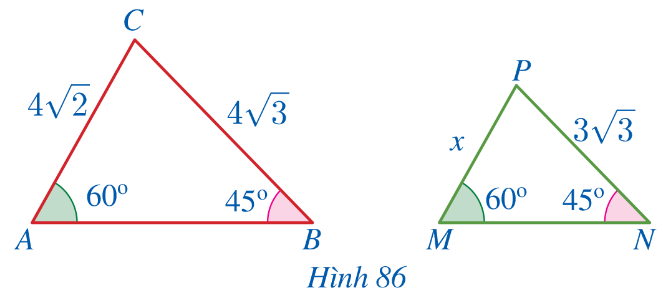
Giải nhanh:

a) Ta có : = = 60⁰ ; = = 45⁰ suy ra △MNP ᔕ △ABC (g.g)

b) △MNP ᔕ △ABC nên = hay = => x = 3

Bài 2: Cho hai tam giác ABC và PMN thỏa mãn = 70⁰ ; = 80⁰; = 80⁰; = 30⁰.Chứng minh = =

Giải nhanh:

Tam giác MNP có + + = 180⁰ mà = 80⁰; = 30⁰ => = 70⁰

= = 70⁰ ; = = 80⁰ => △ABC  ᔕ △PMN (g.g) Do đó = =

Bài 3: Cho tam giác nhọn ABC, hai đường cao AD và BE cắt nhau tại H. Chứng minh:

a) △ACD ᔕ △BCE và CA.CE = CB.CD;

b) △ACD ᔕ △AHE và AC.AE = AD.AH. 

Giải nhanh:

a) Ta có : = = 90⁰; chung góc C suy ra △ACD ᔕ △BCE (g.g) 

do đó = hay CA.CE = CB.CD

b) Ta có : = = 90⁰; chung góc A suy ra △ACD ᔕ △AHE (g.g) 

do đó = hay AC.AE = AD.AH

Bài 4: Cho Hình 87 với = . Chứng minh:

a) △OAD ᔕ  △OCB;              b)  =            c) △OAC ᔕ △ODB.

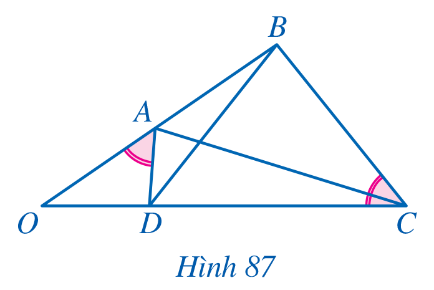
Giải nhanh:

a) Ta có : = ,  chung góc O suy ra △OAD ᔕ  △OCB( g.g)

b) △OAD ᔕ  △OCB nên =  hay =

c) = (cmt) và chung góc O => △OAC ᔕ △ODB (c.g.c)

Bài 5: Cho tam giác ABC vuông tại A, đường cao AH (Hình 88). Chứng minh:

a) △ABC  ᔕ △HBA; AB² = BC . BH;    b) △ABC ᔕ △HAC; AC² = BC . CH;

c) △ABH ᔕ △CAH; AH²  = BH . CH;     d) =  

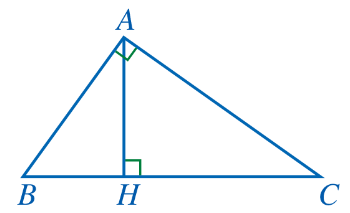
Giải nhanh:

a) Ta có : = = 90⁰; chung góc B=> △ABC  ᔕ △HBA

Do đó : = hay AB² = BC . BH

b) Ta có : = = 90⁰; chung góc C => △ABC  ᔕ △HAC

Do đó : = hay AC² = BC . CH

c) Ta có  △ABC  ᔕ △HBA mà △ABC  ᔕ △HAC

=>  △ABH  ᔕ △CAH do đó = hay AH² = BH. CH

d) Ta có: AB² = BC . BH => = ; AC² = BC . CH => =

              AH² = BH . CH => = (1)

 Ta có : + = + = = = (2)

Từ (1)(2): =

Bài 6: Trong Hình 89, bạn Minh dùng một dụng cụ để đo chiều cao của cây. Cho biết khoảng cách từ mắt bạn Minh đến cây và đến mặt đất lần lượt là AH = 2,8 m và AK = 1,6 m. Em hãy tính chiều cao của cây.

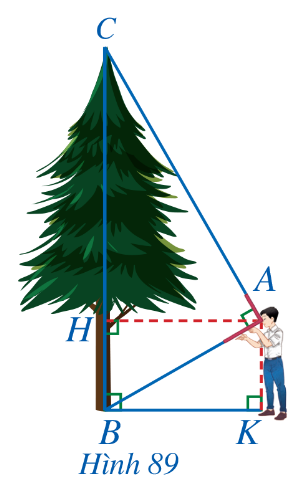
Giải nhanh:

Chiều cao của cây là đoạn thẳng BC. Ta có: AK = BH = 1,6 m

Tam giác AHB vuông tại H: AB² = AH² + BH² = 2,8² + 1,6² = 10,4 => AB =

Ta có : = = 90⁰; chung góc B => △HBA ᔕ △ABC do đó =

Suy ra BC = = 6,5 (m)