Dễ hiểu giải toán 8 cánh diều Bài 4 Hình bình hành
Giải dễ hiểu Bài 4 Hình bình hành. Trình bày rất dễ hiểu, nên tiếp thu Toán 8 Cánh diều dễ dàng. Học sinh nắm được kiến thức và biết suy rộng ra các bài tương tự. Thêm 1 dạng giải mới để mở rộng tư duy. Danh mục các bài giải trình bày phía dưới
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 4. HÌNH BÌNH HÀNH (2 tiết)
I. Định nghĩa
Hoạt động 1 trang 105 sgk Toán 8 tập 1 CD: Cho biết các cặp cạnh đối AB và CD, AD và BC của tứ giác ABCD ở Hình 35 có song song với nhau hay không.
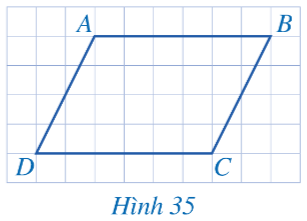
Giải nhanh:
![]() .
.
II. Tính chất
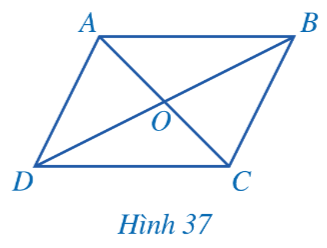
Hoạt động 2 trang 106 sgk Toán 8 tập 1 CD: Cho hình bình hành ABCD (Hình 37).
a) Hai tam giác ABD và CDB có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thắng: AB và CD; DA và BC.
b) So sánh các cặp góc: ![]() ;
; ![]()
c) Hai tam giác OAB và OCD có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: OA và OC; OB và OD.
Giải nhanh:
a) ![]() là hình bình hành nên
là hình bình hành nên ![]() ;
; ![]() .=>
.=> ![]() ;
; ![]()
Xét ![]() và
và ![]() có:
có: ![]() ;
; ![]() ;
; ![]() chung
chung
=> ![]() (g.c.g) =>
(g.c.g) => ![]() và
và ![]()
b) ![]() =>
=> ![]()
Tương tự ta có: ![]() (g.c.g) =>
(g.c.g) => ![]()
c) Xét ![]() và
và ![]() có:
có: ![]()
=> ![]() (g.c.g) =>
(g.c.g) => ![]() và
và ![]() .
.
Luyện tập 1 trang 106 sgk Toán 8 tập 1 CD: Cho hình bình hành ABCD có ![]() =
=![]() , AB = 4 cm, BC = 5 cm. Tính số đo mỗi góc và độ dài các cạnh còn lại của hình bình hành ABCD.
, AB = 4 cm, BC = 5 cm. Tính số đo mỗi góc và độ dài các cạnh còn lại của hình bình hành ABCD.
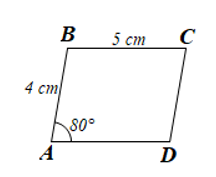
Giải nhanh:
Do ![]() là hình bình hành nên:
là hình bình hành nên: ![]() ;
; ![]() ;
; ![]() ;
; ![]()
Có: ![]() =>
=> ![]() =>
=> ![]()
![]()
III. Dấu hiệu nhận biết
Hoạt động 3 trang 106 sgk Toán 8 tập 1 CD:
a) Cho tứ giác ABCD có AB = CD, BC = DA (Hình 39).
- Hai tam giác ABC và CDA có bằng nhau hay không? Từ đó, hãy so sánh các cặp góc: ![]() ;
; ![]()
- ABCD có phải là hình bình hành hay không?
b) Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường (Hình 40).
- Hai tam giác ABO và CDO có bằng nhau hay không? Từ đó, hãy so sánh các cặp góc:
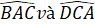 ;
; 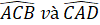
- ABCD có phải là hình bình hành hay không?
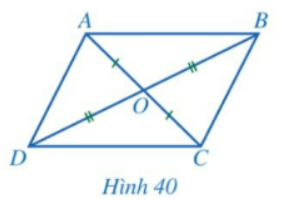
Giải nhanh:
a) Xét ![]() và
và ![]() có:
có: ![]() (gt);
(gt); ![]() (gt);
(gt); ![]() chung
chung
=> ![]() (c.c.c) =>
(c.c.c) => ![]() và
và ![]()
Ta có: ![]() ở vị trí so le trong =>
ở vị trí so le trong => ![]() và
và ![]() ở vị trí so le trong =>
ở vị trí so le trong => ![]()
Tứ giác ![]() có
có ![]() và
và ![]() nên là hình bình hành.
nên là hình bình hành.
b) Xét ![]() và
và ![]() có:
có: ![]() (gt);
(gt); ![]() (đối đỉnh);
(đối đỉnh); ![]() (gt)
(gt)
=> ![]() (c.g.c) =>
(c.g.c) => ![]()
Tương tự ta có: ![]() (c.g.c) =>
(c.g.c) => ![]()
Ta có: ![]() => ABCD là hình bình hành
=> ABCD là hình bình hành
Luyện tập 2 trang 107 sgk Toán 8 tập 1 CD: Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O thoả mãn OA = OC và ![]() . Chứng minh tứ giác ABCD là hình bình hành.
. Chứng minh tứ giác ABCD là hình bình hành.
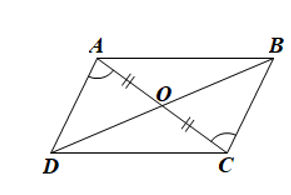
Giải nhanh:
Xét ![]() và
và ![]() có:
có: ![]() (gt);
(gt); ![]() (gt);
(gt); ![]() (đối đỉnh).
(đối đỉnh).
=> ![]() (g.c.g) =>
(g.c.g) => ![]() =>
=> ![]() là hình bình hành.
là hình bình hành.
IV. Bài tập
Bài 1 trang 107 sgk Toán 8 tập 1 CD: Cho tứ giác ABCD có ![]() =
= ![]() . Kẻ tia Ax là tia đối của tia AB. Chứng minh:
. Kẻ tia Ax là tia đối của tia AB. Chứng minh:
a) ![]() b)
b) ![]() ,
, ![]()
c) Tứ giác ![]() là hình bình hành
là hình bình hành
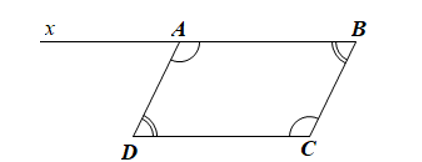
Giải nhanh:
a) ![]() ;
; ![]() =>
=> ![]()
b) Có : ![]() ; mà
; mà ![]()
=> ![]() , hai góc này ở vị trí đồng vị nên =>
, hai góc này ở vị trí đồng vị nên => ![]() .
.
c) Xét tứ giác ![]() có :
có : ![]() =>
=> ![]() là hình bình hành
là hình bình hành
Bài 2 trang 108 sgk Toán 8 tập 1 CD: Cho tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G. Gọi P và Q lần lượt là trung điểm của GB và GC. Chứng minh tứ giác PQMN là hình bình hành.
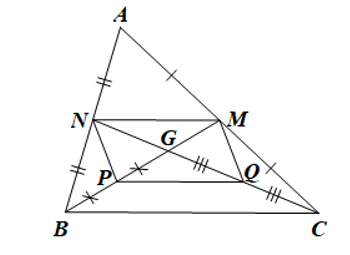
Giải nhanh:
![]() có :
có : ![]() =>
=> ![]() là trọng tâm
là trọng tâm ![]() =>
=> ![]() (1)
(1)
![]() là trung điểm
là trung điểm ![]() =>
=>![]() (2); Q là trung điểm
(2); Q là trung điểm ![]() =>
=> ![]() (3)
(3)
Từ (1)(2)(3) => ![]() và
và ![]() => tứ giác
=> tứ giác ![]() là hình bình hành.
là hình bình hành.
Bài 3 trang 108 sgk Toán 8 tập 1 CD: Cho hai hình bình hành ABCD và ABMN (Hình 42). Chứng minh:
a) CD = MN b) ![]() +
+ ![]() =
= ![]()
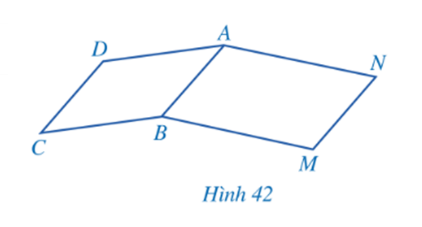
Giải nhanh:
a) Vì ![]() là hình bình hành (gt) =>
là hình bình hành (gt) => ![]() (1);
(1); ![]() là hình bình hành (gt) =>
là hình bình hành (gt) => ![]() (2)
(2)
Từ (1)(2) => ![]()
b) Vì ![]() là hình bình hành =>
là hình bình hành => ![]() (3);
(3); ![]() là hình bình hành =>
là hình bình hành => ![]() (4) Mà
(4) Mà ![]() (5)
(5)
Từ (3)(4)(5) => ![]()
Bài 4 trang 108 sgk Toán 8 tập 1 CD: Để đo khoảng cách giữa hai vị trí A, B ở hai phía của một toà nhà mà không thể trực tiếp đo được, người ta làm như sau: Chọn các vị trí O, C, D sao cho O không thuộc đường thẳng AB; khoảng cách CD là đo được: O là trung điểm của cả AC và BD (Hình 43). Người ta đo được CD = 100 m. Tính độ dài của AB.
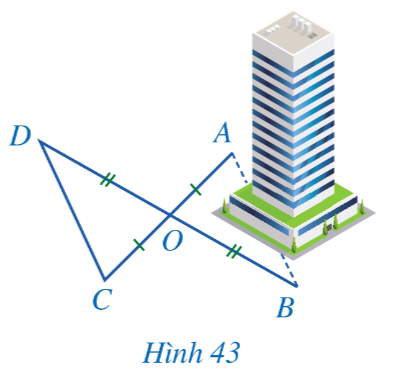
Giải nhanh:
Ta thấy ![]() và
và ![]() ;
;
Mà ![]() và
và ![]() là hai đường chéo của tứ giác
là hai đường chéo của tứ giác ![]() =>
=> ![]() là hình hành
là hình hành
=> ![]()
Bài 5 trang 108 sgk Toán 8 tập 1 CD: Bạn Hoa vẽ tam giác ABC lên tờ giấy sau dó cắt một phần tam giác ở phía góc C (Hình 44). Bạn Hoa đố bạn Hùng: Không vẽ lại tam giác ABC, làm thế nào tính được độ dài các đoạn thẳng AC, BC và số đo góc ACB?
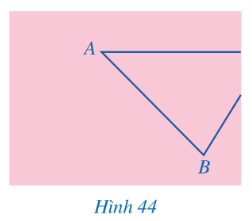
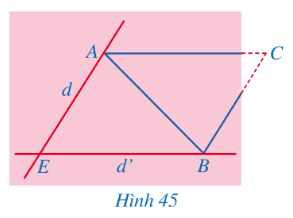
Giải nhanh:
+ Vì ![]() =>
=> ![]() ;
;![]() =>
=> ![]()
+ Xét tứ giác ![]() có :
có : ![]() và
và ![]()
=> ![]() là hình bình hành =>
là hình bình hành => 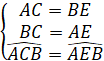
Bạn Hùng chứng minh được tứ giác ![]() là hình bình hành. Từ đó, tính được độ dài các đoạn thẳng
là hình bình hành. Từ đó, tính được độ dài các đoạn thẳng ![]() và số đo
và số đo ![]() .
.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây

Bình luận