BÀI 4. TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC

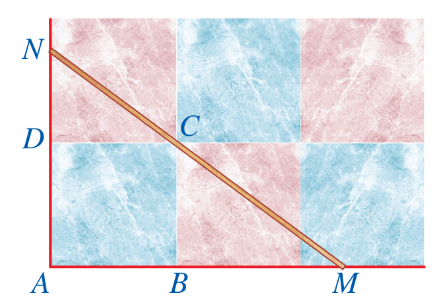
Bài 1: Hính 37 minh họa một phần sân nhà bạn Duy được lát bởi các viên gạch hình vuông khít nhau, trong đó các điểm A, B, C, D là bốn đỉnh của một viên gạch. Bạn Duy đặt một thước gỗ trên mặt sân sao cho thước gỗ luôn đi qua điểm C và cắt tia AB tại M, cắt tia AD tại N. Bạn Duy nhận thấy ta luôn có tỉ lệ thức .

Tại sao ta luôn có tỉ lệ thức ?

Giải nhanh:

+ là đường phân giác trong .

+ Áp dụng tính chất đường phân giác:   

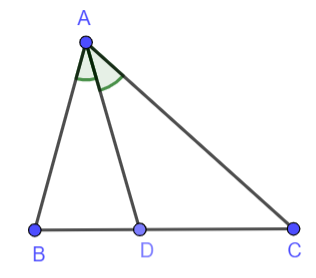
Bài 2: Cho tam giác ABC có AB < AC, AD là đường phân giác. 

Chứng minh DB < DC. 

Giải nhanh:

Xét có là đường phân giác=>

Mà => => => .

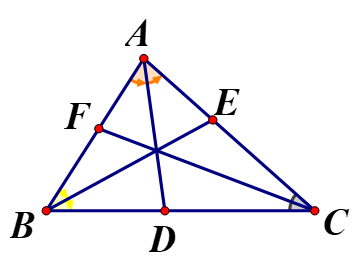
Bài 3: Cho tam giác ABC có ba đường phân giác AD, BE, CF.

 Chứng minh = 1

Giải nhanh:

Xét có là đường phân giác nên ; ;

Ta có:

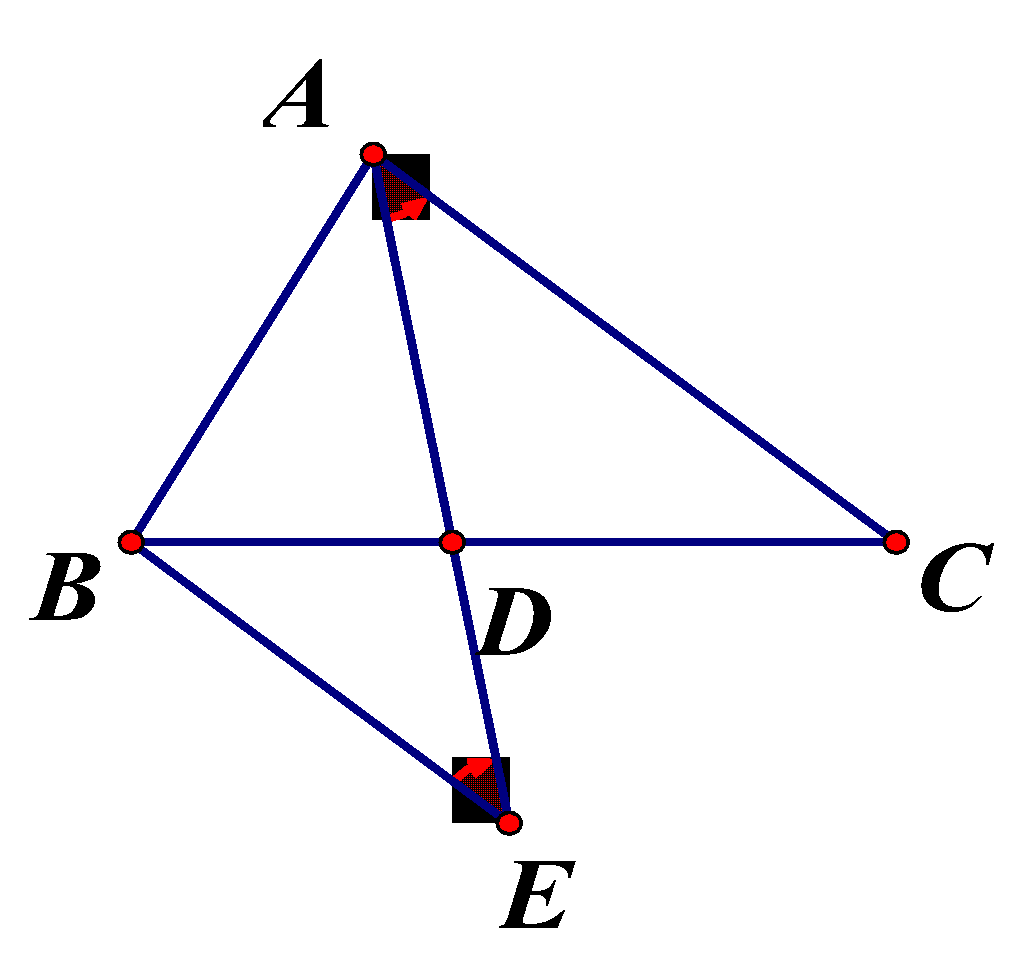
Bài 4: Cho tam giác ABC, điểm D thuộc cạnh BC sao cho . Chứng minh AD là tia phân giác của góc BAC. 

Giải nhanh:

Lấy thuộc sao cho , có:

Mà nên =>

Khi đó cân tại =>

Mà nên => => là phân giác của góc .

BÀI TẬP CUỐI SGK

Bài 1: Cho tam giác ABC có ba đường phân giác AD, BE, CF. Biết AB = 4, BC = 5, CA = 6. Tính BD, CE, AF.

Giải nhanh:

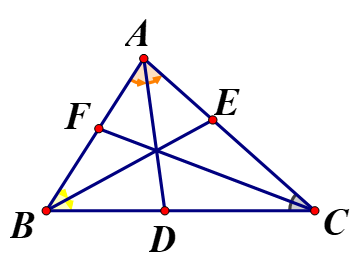
Xét có là đường phân giác nên ; ;

+)                 +)

Từ   Suy ra         =>

+) ; Từ  Suy ra =>

Bài 2:  Cho tam giác ABC có đường trung tuyến AM. Tia phân giác của góc ABC lần lượt cắt các đoạn thẳng AM, AC tại điểm D, E. Chứng minh

Giải nhanh:

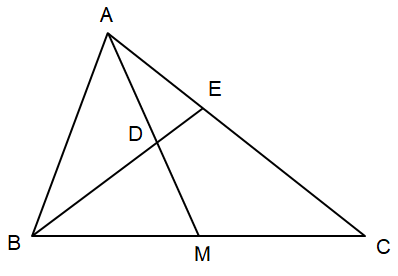
có là đường phân giác nên

là trung điểm của nên => (1)

có là phân giác nên (2)

Từ (1)(2) =>

Bài 3: Quan sát Hình 43 và chứng minh =

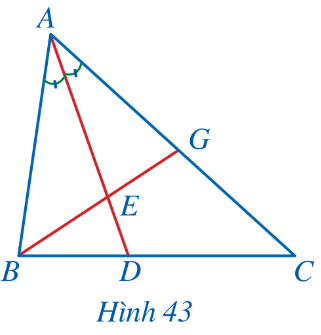
Giải nhanh:

Tam giác ABC có AD là phân giác: ; Tam giác ABG có AE là phân giác: =  =>  : =  

Bài 4: Cho hình thoi ABCD (Hình 44). Điểm M thuộc cạnh AB thỏa mãn AB = 3AM. Hai đoạn thẳng AC và DM cắt nhau tại N. Chứng minh ND = 3MN. 

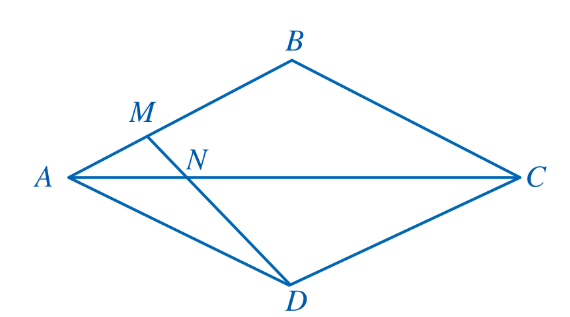
Giải nhanh:

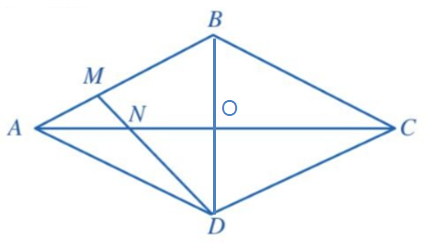
Gọi nên tại

cân tại có là đường cao nên cũng là đường phân giác

có là đường phân giác => (1)

Ta có : mà => (2)

Từ (1)(2) suy ra hay =>

Bài 5: Cho tam giác ABC vuông tại A có AB = 3, AC = 4, AD là đường phân giác. Tính: 

a) Độ dài các đoạn thẳng BC, DB, DC;

b) Khoảng cách từ điểm D đến đường thẳng AC;

c) Độ dài đường phân giác AD. 

Giải nhanh:

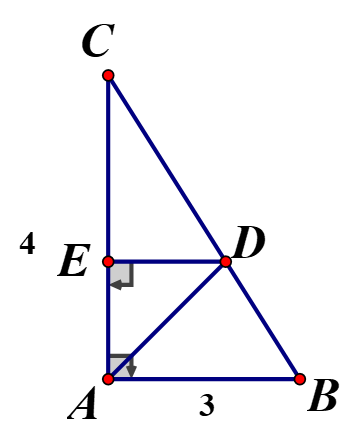
a) + Áp dụng định lí Pythagore trong : BC = 5 cm 

    + Áp dụng tính chất đường phân giác trong , ta có :

    + DC = BC – DB => hay => DB = ; DC =

b) Gọi là chân đường vuông góc kẻ từ đến  

Ta có =>  =>  =>  

c) Xét có nên => =>

vuông tại nên ta có :

Bài 6: Cho tứ giác ABCD với các tia phân giác của các góc CAD và CBD cùng đi qua điểm E thuộc cạnh CD (Hình 45). Chứng minh AD.BC = AC.BD. 

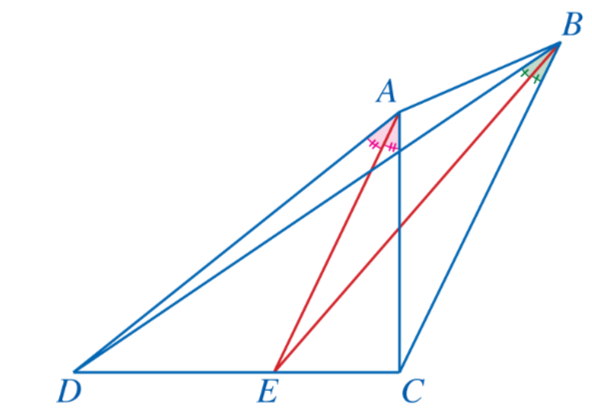
Giải nhanh:

ACD có AE là phân giác => ; BCD có BE là phân giác =>

=>  hay (đpcm)