BÀI 5. TAM GIÁC ĐỒNG DẠNG

I. ĐỊNH NGHĨA

Bài 1: Cho △A'B'C' ᔕ △ABC và AB = 3, BC = 2, CA = 4, A'B' = x, B'C' = 3, C'A' = y. Tìm x và y.

Giải nhanh:

Ta có: △A'B'C' ᔕ △ABC => = = => = = => x = 4,5 ; y = 6

II. TÍNH CHẤT

Bài 1: Cho tam giác ABC. Gọi B', C' lần lượt là trung điểm của AB, AC. Chứng minh △AB'C' ᔕ △ABC.

Giải nhanh:

Ta có: B', C' lần lượt là trung điểm của AB, AC.

Suy ra: B'C' là đường trung bình của tam giác ABC nên B'C' // BC. 

Do đó: △AB'C' ᔕ △ABC.

BÀI TẬP CUỐI SGK

Bài 1: Cho △ABC ᔕ △MNP và = 45⁰ ; = 60⁰.Tính các góc C, M, N, P.

Giải nhanh:

△ABC ᔕ △MNP => = = 45⁰ = = 60⁰ ; = = 75⁰

Bài 2: Cho △ABC ᔕ △MNP và AB = 4, BC = 6, CA = 5, MN = 5. Tính độ dài các cạnh NP, PM. 

Giải nhanh:

Ta có: △ABC ᔕ △MNP => = =  hay  = =

NP = 5.6 : 4 = 7,5;   PM = 5.5 : 4 = 6,25

Bài 3: Ba vị trí A, B, C trong thực tiễn lần lượt được mô tả bởi ba đỉnh của tam giác A'B'C' trên bản vẽ. Biết tam giác A'B'C' đồng dạng với tam giác ABC theo 

tỉ số và A'B' = 4 cm, B'C' = 5 cm, C'A' = 6 cm. Tính khoảng cách giữa hai vị trí A và B, B và C, C và A trong thực tiễn (theo đơn vị kilômét). 

Giải nhanh:

Ta có: △A'B'C' ᔕ △ABC =>   = =  hay = = =

=> AB = 4 000 000 cm = 40 km; BC = 5 000 000 cm = 50 km; CA = 6 000 000 cm = 60 km

Bài 4: Trong Hình 54, độ rộng của khúc sông được tính bằng khoảng cách giữa hai vị trí C, D. Giả sử chọn được các vị trí A, B, E sao cho △ABE ᔕ △ACD và đo được AB = 20m, AC = 50 m, BE = 8 m. Tính độ rộng của khúc sông đó.

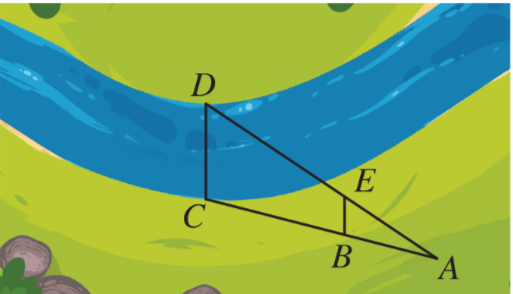
Giải nhanh:

Ta có: △ABE ᔕ △ACD => = =  hay  = => CD = 20 m

Bài 5: Cho tam giác ABC. (Hình 55), các điểm M, N thuộc cạnh AB thỏa mãn AM = MN = NB, các điểm P, Q thuộc cạnh AC thỏa mãn AP = PQ = QC. Tam giác AMP đồng dạng với những tam giác nào?

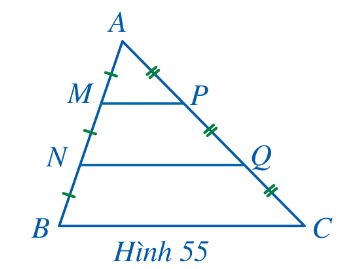
Giải nhanh:

tam giác ANQ và tam giác ABC.

Bài 6: Cho hình bình hành ABCD. Một đường thẳng đi qua D lần lượt cắt đoạn thẳng BC và tia AB tại M và N sao cho điểm M nằm giữa hai điểm B và C. Chứng minh: 

a) △NBM ᔕ △NAD;     b) △NBM ᔕ △DCM;    c) △NAD ᔕ △DCM.

Giải nhanh:

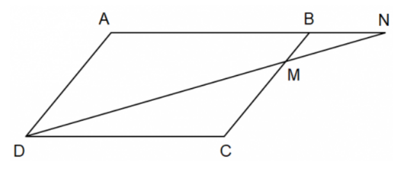
a) Ta có: AD // BC mà M thuộc BC nên BM // AD => △NBM ᔕ △NAD.

b) Ta có: AB // CD mà N thuộc AB nên BN // CD => △NBM ᔕ △DCM.

c) △NBM ᔕ △NAD và △NBM ᔕ △DCM  => △NAD ᔕ △DCM.