BÀI 4. HÌNH BÌNH HÀNH (2 tiết)

I. Định nghĩa

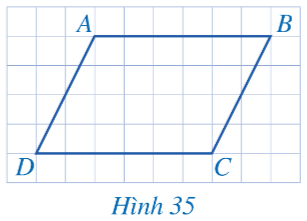
HĐ 1. Cho biết các cặp cạnh đối AB và CD, AD và BC của tứ giác ABCD ở Hình 35 có song song với nhau hay không.

Đáp án chuẩn:

.

II. Tính chất

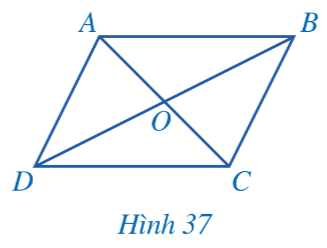
HĐ 2. Cho hình bình hành ABCD (Hình 37).

a) Hai tam giác ABD và CDB có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thắng: AB và CD; DA và BC.

b) So sánh các cặp góc: ;

c) Hai tam giác OAB và OCD có bằng nhau hay không? Từ đó, hãy so sánh các cặp đoạn thẳng: OA và OC; OB và OD.

Đáp án chuẩn:

a)  và

b) ;

c) và .

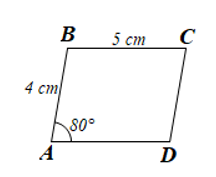
Luyện tập 1. Cho hình bình hành ABCD có =, AB = 4 cm, BC = 5 cm. Tính số đo mỗi góc và độ dài các cạnh còn lại của hình bình hành ABCD.

Đáp án chuẩn:

;

III. Dấu hiệu nhận biết

HĐ 3.

a) Cho tứ giác ABCD có AB = CD, BC = DA (Hình 39).

• Hai tam giác ABC và CDA có bằng nhau hay không? Từ đó, hãy so sánh các cặp góc: 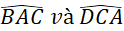và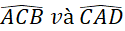

• ABCD có phải là hình bình hành hay không?

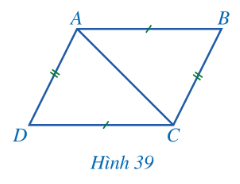
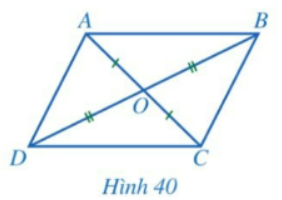
b) Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường (Hình 40).

• Hai tam giác ABO và CDO có bằng nhau hay không? Từ đó, hãy so sánh các cặp góc: ;

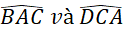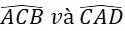
• ABCD có phải là hình bình hành hay không?

Đáp án chuẩn:

a) và

Tứ giác có và nên là hình bình hành.

b)  ;  

Tứ giác có và nên là hình bình hành.

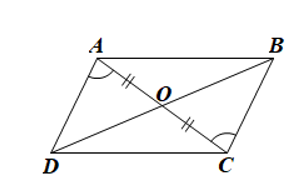
Luyện tập 2. Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O thoả mãn OA = OC và . Chứng minh tứ giác ABCD là hình bình hành.

Đáp án chuẩn:

Xét tứ giác có hai đường chéo và cắt nhau tại trung điểm của mỗi đường => là hình bình hành.

IV. Bài tập

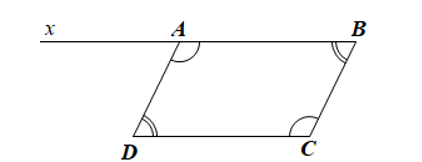
Bài 1: Cho tứ giác ABCD có = . Kẻ tia Ax là tia đối của tia AB. Chứng minh: 

a)

b) ;

c) Tứ giác là hình bình hành.

Đáp án chuẩn:

a) =>

b)  (cùng kề =>

c) => là hình bình hành.

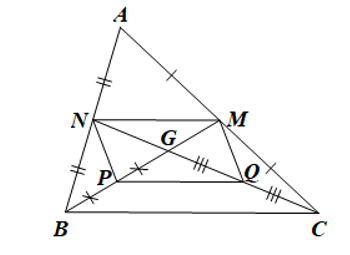
Bài 2: Cho tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G. Gọi P và Q lần lượt là trung điểm của GB và GC. Chứng minh tứ giác PQMN là hình bình hành.

Đáp án chuẩn:

có hai đường chéo và cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.

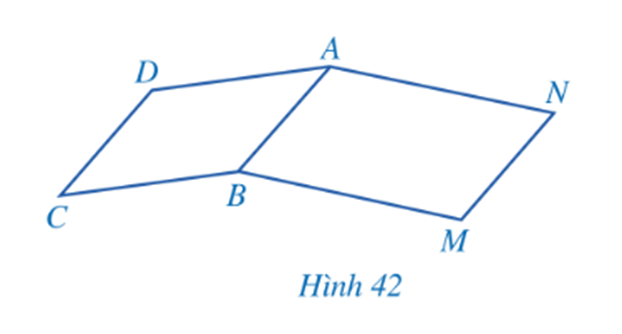
Bài 3: Cho hai hình bình hành ABCD và ABMN (Hình 42). Chứng minh:

a) CD = MN

b) + =

Đáp án chuẩn:

a) ;   =>

b) ; mà  

=>

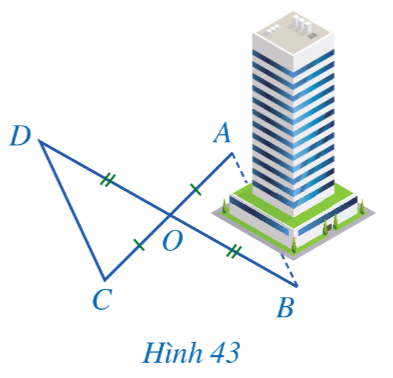
Bài 4: Để đo khoảng cách giữa hai vị trí A, B ở hai phía của một toà nhà mà không thể trực tiếp đo được, người ta làm như sau: Chọn các vị trí O, C, D sao cho O không thuộc đường thẳng AB; khoảng cách CD là đo được: O là trung điểm của cả AC và BD (Hình 43). Người ta đo được CD = 100 m. Tính độ dài của AB.

Đáp án chuẩn:

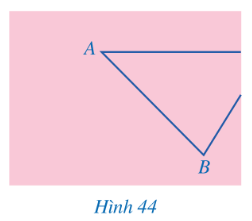
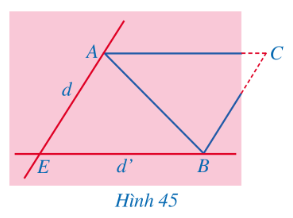
Bài 5: Bạn Hoa vẽ tam giác ABC lên tờ giấy sau dó cắt một phần tam giác ở phía góc C (Hình 44). Bạn Hoa đố bạn Hùng: Không vẽ lại tam giác ABC, làm thế nào tính được độ dài các đoạn thẳng AC, BC và số đo góc ACB?

Đáp án chuẩn:

Bạn Hùng chứng minh được tứ giác là hình bình hành có các tính chất trên, đo độ dài các đoạn thẳng , và đo . Từ đó, tính được độ dài các đoạn thẳng và số đo .