BÀI 3. HÌNH THANG CÂN (2 tiết)

I. Định nghĩa

HĐ 1. Cho biết hai cạnh AB và CD của tứ giác ABCD ở Hình 22 có song song với nhau hay không.

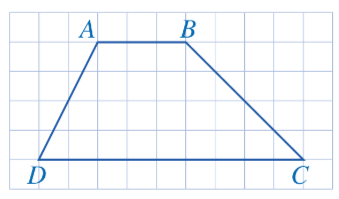
Đáp án chuẩn:

HĐ 2. Hai góc C và D cùng kề với đáy CD của hình thang ABCD ở Hình 23. Cho biết hai góc C và D có bằng nhau hay không.

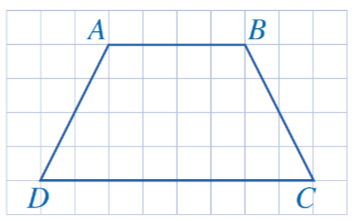
Đáp án chuẩn:

bằng nhau

II. Tính chất

HĐ 3. Cho hình thang cân ABCD có AB // CD, AB < CD, E là giao điểm của AD và BC (Hình 25).

a) So sánh các cặp góc: và : và .

b) So sánh các cặp đoạn thẳng: EA và EB; ED và EC. Từ đó, hãy so sánh AD và BC.

c) Hai tam giác ADC và BCD có bằng nhau hay không? Từ đó, hãy so sánh AC và BD.

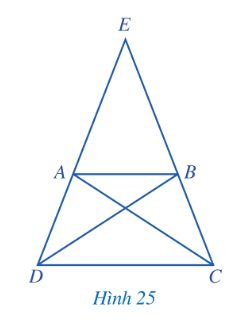
Đáp án chuẩn:

a)  ;

b)

c)

Luyện tập 1. Cho hình thang cân ABCD có AB//CD. Chứng minh .

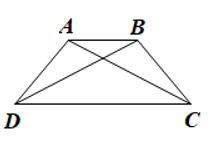
Đáp án chuẩn:

(c.c.c) => .

III. Dấu hiệu nhận biết

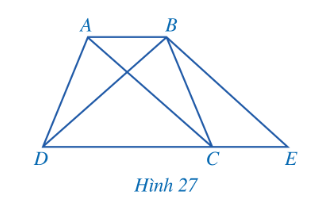
HĐ 4. Quan sát hình thang ABCD (AB // CD, AB < CD) có hai đường chéo AC và BD bằng nhau. Kẻ BE song song với AC (E thuộc đường thẳng CD) (Hình 27).

a) Hai tam giác ABC và ECB có bằng nhau hay không?

b) So sánh các cặp góc: ;

c) Hai tam giác ACD và BDC có bằng nhau hay không? Từ đó, hãy so sánh  

d) ABCD có phải là hình thang cân hay không?

Đáp án chuẩn:

a) Xét và có: chung;

=> (g.c.g)

b) cân tại =>

Có => (đồng vị).

c) Xét và có: chung; ; (gt)

=> (c.g.c)

=>

d) là hình thang cân.

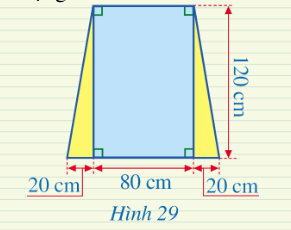
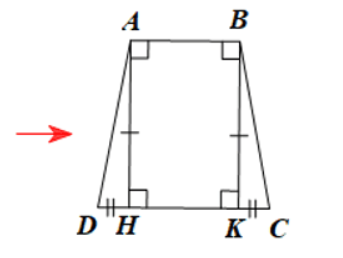
Luyện tập 2. Một ô cửa số có dạng hình chữ nhật với chiêu dài là 120 cm và chiêu rộng là 80 cm. Người ta mở rộng ô cửa số đó bằng cách tăng độ dài cạnh dưới về hai bên, mỗi bên 20 cm (mô tả ở Hình 29). Sau khi mở rộng thì ô cửa số đó có dạng hình gì? Tính diện tích của ô cửa số đó sau khi mở rộng.

Đáp án chuẩn:

IV. Bài tập

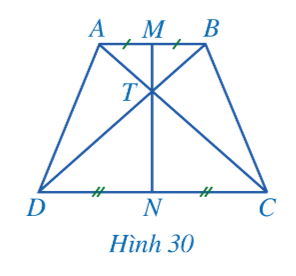
Bài 1: Cho hình thang cân ABCD có AB // CD, AB < CD. Gọi M, N lần lượt là trung điểm của AB, CD và T là giao điểm của AC và BD (Hình 30).

Chứng minh:

1. ,

2. 

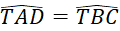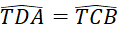
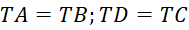
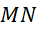3. là đường trung trực củ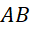a và

Đáp án chuẩn:

a)  => .

=> hay

b)  => ; là trung trực của

=> là đường trung trực của và .

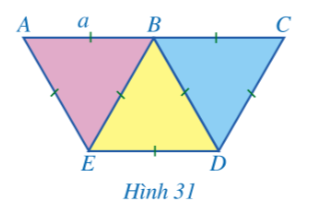
Bài 2: Người ta ghép ba hình tam giác đều có độ dài cạnh là a với vị trí như Hình 31.

a) Chứng minh ba điểm A, B, C thẳng hàng.

b) Chứng minh tứ giác ACDE là hình thang cân.

c) Tính diện tích của tứ giác ACDE theo a.

Đáp án chuẩn:

a) => thẳng hàng.

b)Tứ giác là hình thang có

=> Tứ giác là hình thang cân.

c) 

=> (đvdt)

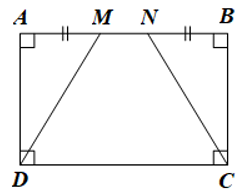
Bài 3: Cho hình chữ nhật ABCD. Trên cạnh AB lấy hai điểm M, N sao cho AM = NB < AB. Chứng minh tứ giác MNCD là hình thang cân.

Đáp án chuẩn:

là hình thang có 

=> Hình thang là hình thang cân.

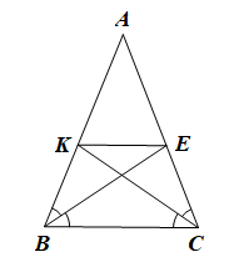
Bài 4: Cho tam giác ABC cân tại A có hai đường phân giác BE và CK. Chứng minh tứ giác BKEC là hình thang cân.

Đáp án chuẩn:

là hình thang có  

=> hình thang là hình thang cân.

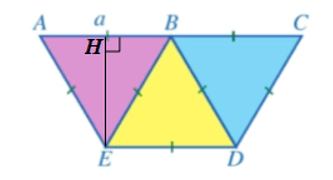
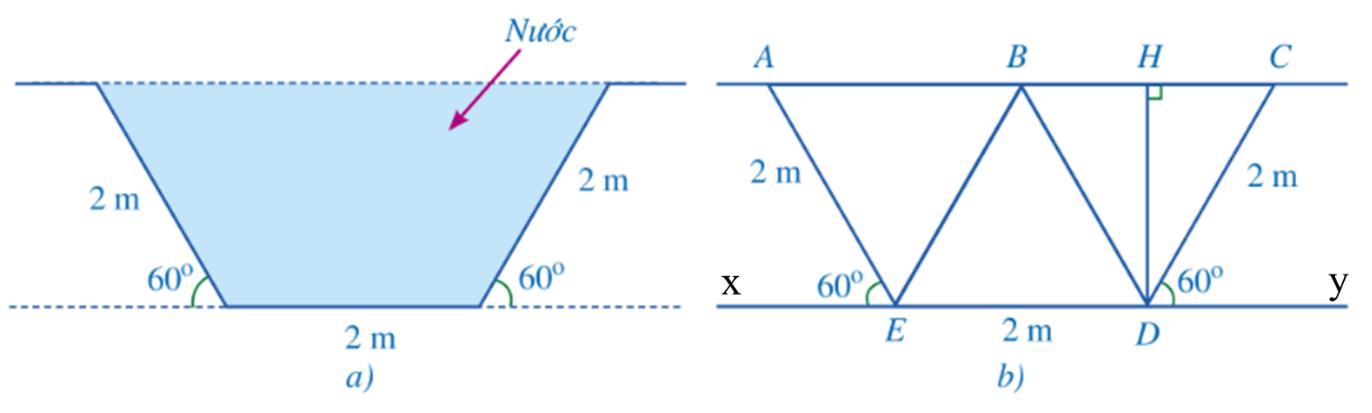
Bài 5: Hình 33a là mặt cắt đứng phần chứa nước của một con mương (Hình 32) khi đây nước có đạng hình thang cân. Người ta mô tả lại bằng hình học mặt cắt đứng của con mương đó ở Hình 33b với BD // AE (B thuộc AC). H là hình chiếu của D trên đường thắng AC.

a) Chứng minh các tam giác BCD, BDE, ABE là các tam giác đều.

b) Tính độ dài của DH, AC.

c) Tính diện tích mặt cắt đứng phần chứa nước của con mương đó khi đầy nước.

Đáp án chuẩn:

a) là tam giác cân có 1 góc bằng => là tam giác đều.

Cmtt được : là các tam giác đều.

b) m

c)