I. ĐỊNH NGHĨA

HĐ1

Ta thấy AB song song với CD.

Định nghĩa: Hình thang là tứ giác có hai cạnh đối song song.

HĐ2

Hai góc C và D của hình thang ABCD bằng nhau.

Định nghĩa: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

Chú ý: Nếu ABCD là hình thang cân (AB // CD) thì $\widehat{A}+\widehat{B}$ và $\widehat{C}+\widehat{D}$.

Ví dụ 1: (SGK – tr.101)

Hướng dẫn giải (SGK – tr.102)

II. TÍNH CHẤT

HĐ3

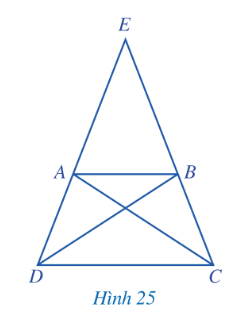
a) ABCD là hình thang cân => $\widehat{ADC}=\widehat{BCD}$ và $\widehat{DAB}=\widehat{CBA}$ (1)

Do $\widehat{ADC}=\widehat{BCD}\Rightarrow \widehat{EDC}=\widehat{ECD}$

Có: $\widehat{DAB}+\widehat{EAB}=180^{o}\Rightarrow \widehat{EAB}=180^{o}-\widehat{DAB}$ (2)

Có: $\widehat{EAB}=180^{o}-\widehat{CBA}$ (3)

Từ (1), (2), (3) => $\widehat{EAB}=\widehat{EBA}$

b) $\Delta EAB$ có $\widehat{EAB}=\widehat{EBA}$

=> ∆EAB cân tại E => ED = EC.

Có: AD = ED - EA; BC = EC - EB

Mà EA = EB và ED = EC

=> AD = BC.

c) Xét ∆ADC và ∆BCD có:

AD = BC ; $\widehat{ADC}=\widehat{BCD}$; DC chung

=> ∆ADC = ∆BCD (c.g.c)

=> AC = BD

Định lí: Trong hình thang cân:

• Hai cạnh bên bằng nhau.
• Hai đường chéo bằng nhau.

Ví dụ 2: (SGK – tr.102)

Hướng dẫn giải (SGK – tr.102).

Luyện tập 1

Ta có: ABCD là hình thang cân => AD = BC và AC = BD

Xét ∆ADB và ∆BCA có:

AB chung; AD = BC; AC = BD

=> ∆ADB = ∆BCA (c.c.c)

=> $\widehat{ADB}=\widehat{BCA}$.

III. DẤU HIỆU NHẬN BIẾT

HĐ4

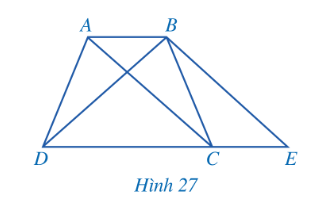
a) AB // CE => $\widehat{ABC}=\widehat{ECB}$ (so le trong)

BE // AC => $\widehat{BEC}=\widehat{ACB}$ (so le trong)

Xét ∆ABC và ∆ECB có:

BC chung; $\widehat{ABC}=\widehat{ECB}$; $\widehat{BEC}=\widehat{ACB}$

=> ∆ABC = ∆ECB (g.c.g)

b) Vì ∆ABC = ∆ECB (g.c.g) => AC = EB; Mà AC = BD

=> BD = BE => ∆BDE cân tại B

=> $\widehat{BDE}=\widehat{BED}$

Có BE // AC => $\widehat{ACD}=\widehat{BED}$ (đồng vị).

c) Có: $\widehat{BDE}=\widehat{BED}$ và $\widehat{ACD}=\widehat{BED}$

=> $\widehat{BDE}=\widehat{ACD}$

Xét ∆ACD và ∆BDC có:

DC chung; $\widehat{BDE}=\widehat{ACD}$; AC = BD (gt)

=> ∆ACD = ∆BDC (c.g.c)

=> $\widehat{ADC}=\widehat{BCD}$

d) Hình thang ABCD có hai góc kề một đáy $\widehat{ADC}=\widehat{BCD}

=> Hình thang ABCD là hình thang cân.

Dấu hiệu nhận biết: Hình thang có hai đường chéo bằng nhau là hình thang cân.

Ví dụ 3: (SGK – tr.103)

Hướng dẫn giải (SGK – tr.103).

Luyện tập 2

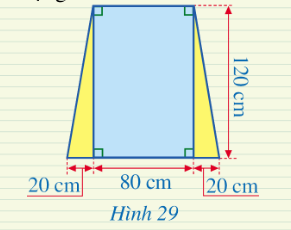
Hướng dẫn giải:

Ô cửa sổ được minh họa lại bằng hình sau:

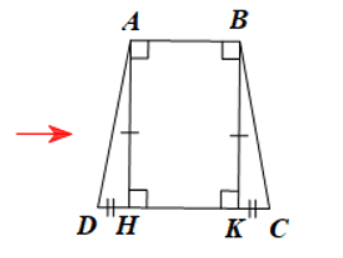
Xét ∆AHD và ∆BKC có:

$\widehat{AHD}=\widehat{BKC}$ (vuông); AH = BK; HD = KC

=> ∆AHD = ∆BKC (c.g.c)

=> $\widehat{ADH}=\widehat{BCK}$

Xét tứ giác ABCD có: AB // DC nên là hình thang.

Mà $\widehat{ADH}=\widehat{BCK}$

=> hình thang ABCD là hình thang cân.

Có: AB = HK = 80 cm

DC = DH + HK + KC = 20 + 80 + 20 = 120 cm

Diện tích cửa sổ sau khi mở rộng:

S = $\frac{1}{2}$.AB+DC.AH 

=1$\frac{1}{2}$.(80 + 120).120 = 12 000 (cm$_{2}$)