BÀI TẬP CUỐI CHƯƠNG VIII

Bài 1: Cho △DEG  ᔕ △MNP ;   = 60⁰ ; = 40⁰

a) Số đo góc D bằng bao nhiêu độ?

          A.40⁰                            B. 50⁰                         C. 60⁰                         D. 80⁰

b) Số đo góc N bằng bao nhiêu độ?

          A.40⁰                            B. 50⁰                         C. 60⁰                         D. 80⁰

c) Số đo góc P bằng bao nhiêu độ?

          A.40⁰                            B. 50⁰                         C. 60⁰                         D. 80⁰

Đáp án chuẩn:

a) A                                         b) C                                         c) D

Bài 2: Cho △DEG  ᔕ △MNP; DE = 2 cm, DG = 4 cm, MN = 4 cm, NP = 6 cm.

a) Độ dài cạnh EG là:

            A. 2 cm                      B. 3 cm                      C. 4 cm                      D. 8 cm

b) Độ dài cạnh MP là:

            A. 2 cm                      B. 3 cm                      C. 4 cm                      D. 8 cm

Đáp án chuẩn: 

a) B                                                                 b) D

Bài 3: Cho tam giác ABC, các điểm M, N, P lần lượt thuộc các cạnh AB, AC, BC sao cho tứ giác BMNP là hình bình hành (Hình 102). 

Chứng minh + =1

Đáp án chuẩn:

+ = + = = = 1

Bài 4: Cho tứ giác ABCD. Tia phân giác của các góc BAD và BCD cắt nhau tại điểm I. Biết I thuộc đoạn thẳng BD (Hình 103). Chứng minh AB.CD = AD. BC

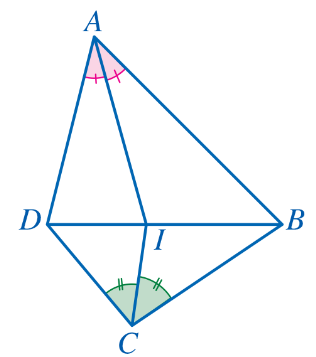
Đáp án chuẩn: 

= ; =  => = hay  AB.CD = AD.BC

Bài 5: Cho hình bình hành ABCD. Gọi M, N, P lần lượt là trung điểm của các đoạn thẳng AB, BC, AN và Q là giao điểm của AN và DM. Chứng minh:

a) MP // AD, MP = AD;

b) AQ = AN;

c) Gọi R là trung điểm của CD. Chứng minh ba điểm M, P, R thẳng hàng và PR = AD. 

Đáp án chuẩn:

a) MP = BN mà BN = BC  nên MP = BC

Mà BC = AD  => MP = AD.

b) AQ = 4.QP;  QP = AN - AQ => AQ = 4(AN - AQ) = 2AN - 4AQ 

=> 5AQ = 2 AN hay AQ = AN

c) Chứng minh M, P, R thẳng hàng.

Ta có: MP = AD Mà MR = AD => MP = MR => PR = AD

Bài 6: Cho tam giác ABC đồng dạng với tam giác A'B'C' theo tỉ số đồng dạng k.

a) Cho AM, A'M' lần lượt là các đường trung tuyến của các tam giác ABC, A'B'C'. Chứng minh △ABM ᔕ △A'B'M' và  = k

b) Cho AD, A'D' lần lượt là các đường phân giác của các tam giác ABC, A'B'C'. Chứng minh △ABD ᔕ △A'B'D' và  = k

c) Cho AH, A'H' lần lượt là các đường cao của các tam giác ABC, A'B'C'. Chứng minh △ABH ᔕ △A'B'H' và = k

Đáp án chuẩn:

a) = = k và = => △ABM ᔕ △A'B'M' (c.g.c) 

=> = = k

b) = và = => △ABD ᔕ △A'B'D'( c.g.c)

=> = k

c) = và = = 90⁰ => △ABH ᔕ △A'B'H' (g.g) 

=> = = k

Bài 7: Tính các độ dài x, y, z, t ở các Hình 104a, 104b, 104c.

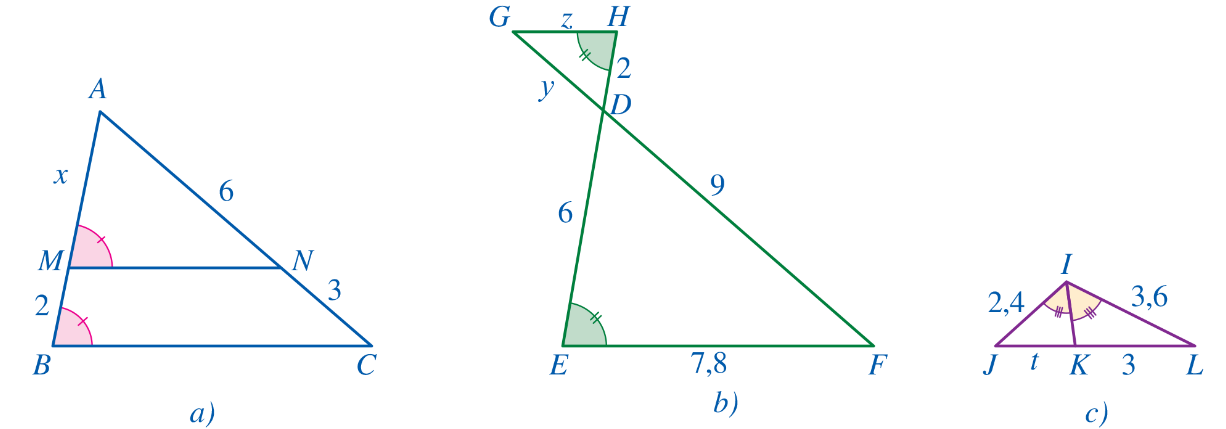
Đáp án chuẩn:

a) x = 4.

b) y = 3 ; z = 2,6

c) t = 2

Bài 8: Cho Hình 105. Chứng minh:

a) △HAB ᔕ  △HBC;                                              b) HB = HD = 6 cm.

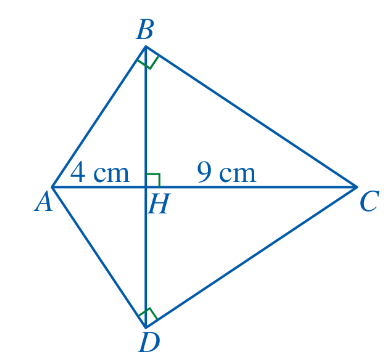
Đáp án chuẩn:

a) △HAB ᔕ  △BAC; △HBC  ᔕ △BAC => △HAB ᔕ △HBC.

b) △HAB ᔕ △HBC => = => HB = 6 (cm)

△HAD ᔕ △HDC => = HD = 6 (cm)

=> HB = HD = 6 cm.

Bài 9: Cho Hình 106. Chứng minh:

a) AH² = AB.AI = AC.AK;                             b) =

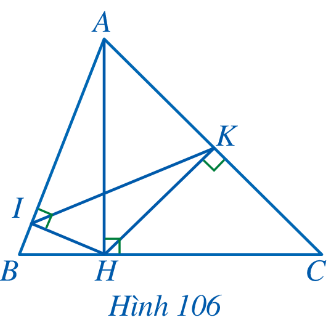
Đáp án chuẩn: 

a) △AIH ᔕ △AHB (g.g) => = => AH² = AB.AI

△AKH ᔕ △AHC (g.g) => = => AH² = AC.AK

Vậy AH² = AB.AI = AC.AK

b) = , chung góc A => △ABC ᔕ △AKI (g.g) => =

Bài 10: Cho tam giác ABC có M, N là hai điểm lần lượt thuộc các cạnh AB, AC sao cho MN // BC. Gọi I, P, Q lần lượt là giao điểm của BN và CM, AI và MN, AI và BC. Chứng minh:

a) = =                                                        b) = =  

Đáp án chuẩn:

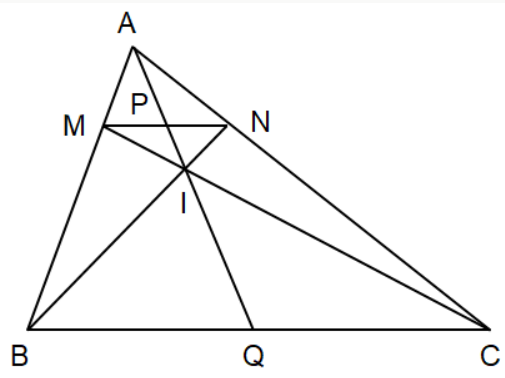
a) = ; = =>  = =

b) = ;  = => = =

Bài 11: Cho Hình 107. Chứng minh:

a) △ABN ᔕ △AIP và AI . AN = AP . AB;

b) AI . AN + BI . BM = AB²

Đáp án chuẩn: 

a) △ABN ᔕ △AIP (g.g) => = => AI.AN = AB.AP

b) △AMB ᔕ △IPB (g.g) => = => BI.BM = AB.BP

Khi đó: AI.AN + BI.BM = AB.AP + AB.BP = AB. (AP + PB) = AB²

Bài 12: Hình 108 minh họa mặt cắt đứng của tủ sách nghệ thuật ở nhà bác Ngọc. Sau một thời gian sử dụng, tủ sách đó đã có dấu hiệu bị xuống cấp và cần sửa lại. Các tấm ngăn BM, CN, DP bị hỏng và cần thay mới. Em hãy giúp bác Ngọc tính toán chiều dài các tấm ngăn mới lần lượt thay thế cho các tấm ngăn BM, CN, DP đã bị hỏng. Biết chiều dài tấm ngăn EQ bằng 4 m. 

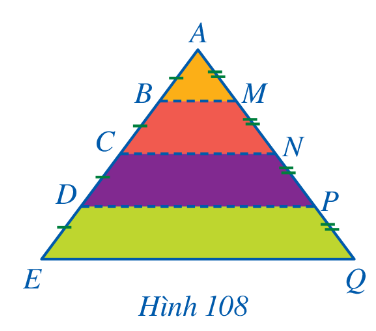
Đáp án chuẩn:

BM = 1; CN = 2; DP = 3

Bài 13: Cho Hình 109. Hình nào đồng dạng phối cảnh với:

a) Tam giác OAB?                           b) Tam giác OBC?

c) Tam giác OCD?                           d) Tứ giác ABCD?

Đáp án chuẩn:

a) △OMN 

b) △ONP 

c) △OPQ 

d) Tứ giác MNPQ 

Bài 14: Hình 110 có ghi thứ tự của 6 lá mầm, trong đó có nhiều cặp lá mầm gợi nên những cặp hình đồng dạng. Hãy viết 6 cặp lá mầm gợi nên những hình đồng dạng.

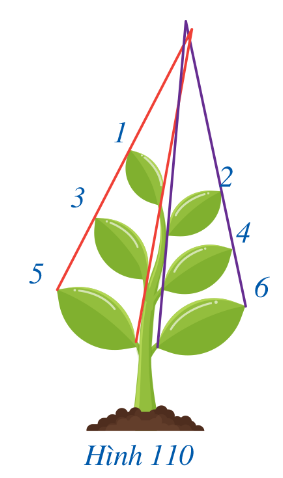
Đáp án chuẩn:

lá 1 và lá 3; lá 3 và lá 5; lá 1 và lá 5; lá 2 và lá 4; lá 4 và lá 6; lá 2 và lá 6