I. Định nghĩa

Bài 1: So sánh độ dài các cạnh của tứ giác ABCD ở hình 56. 

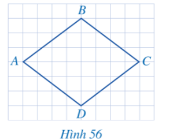
Đáp án:

Tứ giác ABCD Hình 56 có: $AB = BC = CD = DA$

II. Tính chất

Bài 1: Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O (Hình 58).

a) Hình thoi ABCD có là hình bình hành hay không?

b) Hai đường chéo AC và BD có vuông góc với nhau hay không?

c) Hai tam giác ABC và ADC có bằng nhau hay không? Tia AC có phải là tia phân giác của BAD hay không?

Đáp án:

a) Do ABCD là hình thoi $=> AB=BC=CD=DA$

Xét tứ giác $ABCD$ có $AB=CD; AD=BC$

=> ABCD là hình bình hành.

b) Do ABCD là hình bình hành nên $OB=OD$

Xét ∆OAD và ∆OAB có:

$OA$ chung

$AD=AB, OD=OB$

$=> ∆OAD=∆OAB (c.c.c) => \widehat{AOD}=\widehat{AOB}$ (góc tương ứng)

Mà $\widehat{AOD}+\widehat{AOB}=180^{\circ} => \widehat{AOD}=\widehat{AOB}=\frac{180^{\circ}}{2}=90^{\circ}$

hay $AC⊥BD$ tại O.

c) Xét ∆ABC và ∆ADC có:

$AC$ chung

$AB=AD, BC=DC (cmt)$

=> $∆ABC=∆ADC (c.c.c) => \widehat{BAC}=\widehat{DAC}$ nên AC là phân giác $\widehat{BAD}$.

Bài 2: Cho hình thoi $ABCD$ có $\widehat{ABC}=120^{\circ}$. Chứng minh tam giác ABD là tam giác đều.

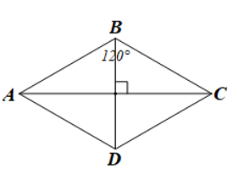
Đáp án:

Xét ∆ABD, có

$AB = AD (ABCD$ là hình thoi)

∆ABD cân tại A. Lại có BD là phân giác $\widehat{ABC}$ (tính chất hình thoi).

=> $\widehat{ABD}=\frac{1}{2}\widehat{ABC}=\frac{1}{2}.120^{\circ}=60^{\circ}$

Vậy ∆ABD là tam giác cân có một góc $\widehat{ABD}=60^{\circ}$ nên là tam giác đều.

III. Dấu hiệu nhận biết

Bài 1:

a) Cho hình bình hành ABCD có hai cạnh kề AB và BC bằng nhau. ABCD có phải là hình thoi hay không?

b) Cho hình bình hành ABCD có hai đường chéo AC và BD vuông góc với nhau (Hình 60):

Đường thẳng AC có phải là đường trung trực của đoạn thẳng BD hay không?

ABCD có phải là hình thoi hay không?

Đáp án:

a) Xét hình bình hành $ABCD$ có: $AB=CD$ và $AD=BC$.

Mà $AB=BC => AB=BC=CD=DA$. Vậy ABCD là hình thoi.

b) 

Ta có AC và BD là 2 đường chéo cắt nhau tại trung điểm mỗi đường (do ABCD là hình bình hành)

=> $AC⊥BD$ tại trung điểm O của BD

=> AC là trung trực của BD.

Vì AC là đường trục trực của $BD => AD=AB$

Xét hình bình hành ABCD có hai cạnh kề $AD = AB$ nên $ABCD$ là hình thoi.

Bài 2: Cho tam giác ABC cân tại A có M là trung điểm BC. Trên tia đối của tia MA lấy điểm N sao cho $MN = MA$. Chứng minh tứ giác ABNC là hình thoi.

Đáp án:

Ta có: $MN=MA => M$ là trung điểm $AN$

Xét tứ giác $ABNC$ có 

AN và BC là hai đường chéo cắt nhau tại trung điểm M mỗi đường.

=> ABNC là hình bình hành.

Mặt khác ∆ABC cân tại A, AM là trung tuyến, cũng là đường cao (gt)

 => $AM⊥BC$ hay $AN⊥BC$.

=> Hình bình hành ABNC có hai đường chéo vuông góc với nhau tại trung điểm mỗi đường nên ABNC là hình thoi

IV. Bài tập

Bài 1: Cho hình bình hành ABCD có tia AC là tia phân giác của góc DAB. Chứng minh ABCD là hình thoi.

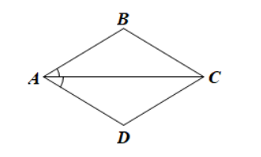
Đáp án:

Ta có: $\widehat{BAC}=\widehat{DAC} (AC$ là phân giác của $\widehat{DAB}$)

$AB//CD (ABCD$ là hình bình hành) => $\widehat{BAC}=\widehat{DCA}$ (so le trong). 

Do đó $\widehat{DAC}=\widehat{DCA}$

Xét ∆DAC có $\widehat{DAC}=\widehat{DCA} => ∆DAC$ cân tại D => $DA=DC$

Hình bình hành ABCD có hai cạnh kề DA và DC bằng nhau nên là hình thoi.

Bài 2: Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Chứng minh:…

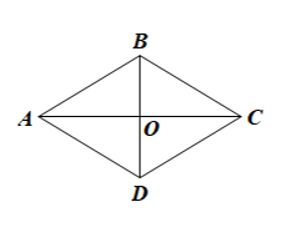
Đáp án:

Ta có : $AC\perp BD$ tại trung điểm O của mỗi đường (ABCD là hình thoi)

=> $AC=2OA;BD=2OB$

Ta có : $AC^2+BD^2=(2OA)^2+(2OB)^2=4OA^2+4OB^2=4(OA^2+OB^2)$

Xét ∆OAB vuông tại O

$AB^2=OA^2+OB^2$ (định lí Pytagore)

=> $AC^2+BD^2=4(OA^2+OB^2)=4AB^2$

Bài 3: Cho hình thoi ABCD có $\widehat{CDB}=40^{\circ}$. Tính số đo mỗi góc của hình thoi ABCD.

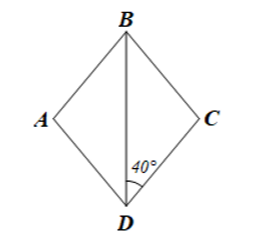
Đáp án:

$ABCD$ là hình thoi nên $BD$ là phân giác $\widehat{ADC}$

=> $\widehat{ADC}=2.40^{\circ}=80^{\circ}$ 

=> $\widehat{ABC}=\widehat{ADC}=80^{\circ}$ 

Ta có: $AB//CD$, do đó $\widehat{BAD}+\widehat{ADC}=180^{\circ}$

=> $\widehat{BAD}=180^{\circ}-\widehat{ADC}=180^{\circ}-80^{\circ}=100^{\circ}$

Do đó $\widehat{BCD}=\widehat{BAD}=100^{\circ}$.

Bài 4: Hình 62 mô tả một ô lưới mắt cáo có dạng hình thoi với độ dài của hai đường chéo là 45 mm và 90 mm. Độ dài cạnh của ô lưới mắt cáo đó là bao nhiêu milimét (làm tròn kết quả đến hàng đơn vị)?

Đáp án:

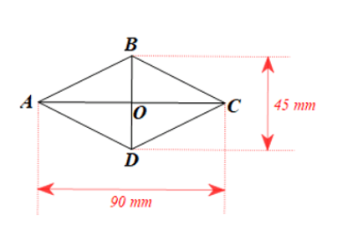
Ta có : $AC và BD$ vuông góc tại trung điểm O của mỗi đường ($ABCD$ là hình thoi).

=> $OA=\frac{1}{2}AC=45 mm; OB=\frac{1}{2}BD=22,5 (mm)$

Xét ∆OAB vuông tại O. 

$AB^2=OA^2+OB^2$ (định lí Pytagore)

= $45^2+22,5^2=2025+506,25=2531,25$

=> $AB=\sqrt{22531,25}≈50 (mm)$

Bài 5: Một viên gạch trang trí có dạng hình thoi với độ dài cạnh là 40 cm và số đo một góc là 60° (Hình 63). Diện tích của viên gạch đó là bao nhiêu centimét vuông (làm tròn kết quả đến hàng phần trăm)?

Đáp án:

Xét ∆BCD có

BC=CD => ∆BCD cân tại C

Mà $\widehat{BCD}=60^{\circ} => ∆BCD$ đều.

=> $BC=CD=BD=40 cm$

Ta có : $AC\perp BD$ tại trung điểm O cả mỗi đường (Do ABCD là hình thoi)

=> $OB=\frac{1}{2}BD=20 (cm)$

Xét ∆OBC vuông tại O. 

$BC^2=OB^2+OC^2$ (định lí Pytagore)

=> $OC^2=BC^2-OB^2=40^2-20^2=1600-400=1200$

=> $OC=\sqrt{1200}≈34,64 (cm)$ 

Mà O là trung điểm $AC => AC≈69,28 (cm)$

$S_{ABCD}=\frac{1}{2}.AC.BD≈\frac{1}{2}.69,28.80=2771,2 cm^2$.