I. Hình chóp tam giác đều

Bài 1: Thực hiện các hoạt động sau:

a) Vẽ trên giấy (hay bìa mỏng) 4 hình tam giác với các cạnh và vị trí như ở Hình 2

b) Cắt rời theo đường viên (màu đỏ), của hình vừa vẽ (phần tô màu) và gấp lại để được hình chóp tam giác đều như ở Hình 3. 

Đáp án:

Học sinh dựa vào hình minh họa vẽ trên giấy 4 hình tam giác bắt đầu từ hình tam giác đều ở giữa trước. Sau đó ở mỗi cạnh tam giác đều, ta sẽ vẽ thêm 3 tam giác cân

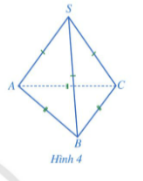
Bài 2: Quan sát hình chóp tam giác đều ở hình 4 và đọc tên các mặt, các cạnh, đỉnh của hình chóp tam giác đều đó. 

Đáp án:

Các mặt là SAB, SBC, SCA, ABC.

Các cạnh đáy AB, BC, CA bằng nhau;

Các cạnh bên SA, SB, SC bằng nhau;

S gọi là đỉnh của hình chóp tam giác đều S.ABC

II. Diện tích xung quanh của hình chóp tam giác đều

Bài 1: Cho một hình chóp tam giác đều có độ dài cạnh đáy bằng 8 cm và độ dài trung đoạn bằng 10 cm. Tính diện tích xung quanh của hình chóp tam giác đều đó.

Đáp án:

$S_{xq}$ của hình chóp tam giác đều đó là:

$S_{xq} = \frac{1}{2}.(8.3).10=120 (cm^2)$.

III. Thể tích của hình chóp tam giác đều

IV. Bài tập

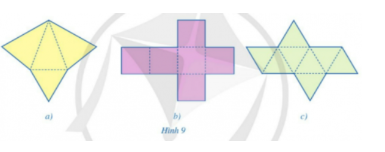
Bài 1: Trong các miếng bìa ở hình 9a, 9b, 9c, miếng bìa nào có thể gấp lại (theo các nét đứt) để được hình chóp tam giác đều?

Đáp án:

Chỉ có miếng bìa 9a có thể gấp lại để được hình chóp tam giác đều do hình 9a có 4 mặt, trong đó có 1 mặt đáy là tam giác đều và 3 mặt bên là các tam giác cân.

Bài 2: Cho hình chóp tam giác đều P.QRS có độ dài cạnh đáy bằng 4 cm và độ dài trung đoạn bằng 10 cm. Tính diện tích xung quanh của hình chóp tam giác đều đó.

Đáp án:

$S_{xq}P.QRS$ là: $S_{xq} = \frac{1}{2}.(4 .3).10=60 cm^2$.

Bài 3: Cho một hình chóp tam giác đều có diện tích đáy là 15 cm2 và chiều cao là 8 cm. Tính thể tích của hình chóp tam giác đều đó.

Đáp án:

Thể tích của hình chóp tam giác đều đó là:

$V = \frac{1}{3}.15.8=40 (cm^3)$.

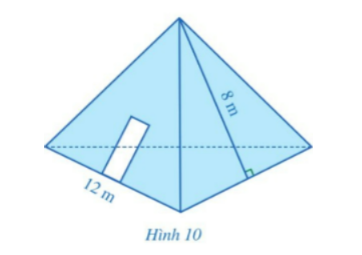
Bài 4: Một kho chứa có dạng hình chóp tam giác đều với độ dài cạnh đáy khoảng 12 m và độ dài trung đoạn khoảng 8 m (Hình 10). Người ta muốn sơn phủ bên ngoài cả ba mặt xung quanh của kho chứa đó và không sơn phủ phần làm cửa có diện tích là 5 m°. Biết rằng cứ mỗi mét vuông sơn cần trả 30 000 đồng. Cần phải trả bao nhiêu tiền để hoàn thành việc sơn phủ đó?

Đáp án:

$S_{xq}$ của kho chứa đó là: $S_{xq} = \frac{1}{2}.(12.3).8 = 144 (m^2)$

Diện tích cần sơn là: $S = 144 – 5 = 139 (m^2)$

Cần trả số tiền để hoàn thành việc sơn phủ đó là: $139 . 30 000 = 4 170 000$ (đồng)