I. Đồ thị của hàm số bậc nhất.

Bài 1: Xét hàm số $y = x - 2$. 

Tìm giá trị của y tương ứng với giá trị của x trong bảng sau: 

Vẽ các điểm $A(0 ; - 2), B(2 ; 0), C(3 ; 1)$ của đồ thị hàm số $y = x - 2$ trong mặt phẳng toạ độ Oxy. Dùng thước thắng để kiểm tra ba điểm A, B, C có thẳng hàng hay không.

Đáp án:

a) 

b) Các điểm A(0 ; - 2), B(2 ; 0), C(3 ; 1) của đồ thị hàm số y = x - 2

Ta thấy ba điểm A, B, C có thẳng hàng.

Bài 2: Cho hàm số $y = 4x + 3$. Tìm điểm thuộc đồ thị của hàm số có hoành độ bằng 0.

Đáp án:

Thay $x = 0$ vào hàm số $y = 4x + 3$, có:

$y = 4.0 + 3 = 3$ 

Vậy điểm cần tìm có tọa độ là (0; 3).

II. Vẽ đồ thị của hàm số bậc nhất

Bài 1: Vẽ đồ thị của mỗi hàm số sau:

a. $y = 3x$

b. $y = 2x + 2$

Đáp án:

Hàm số $y = 3x$

+ Với $x = 0$ thì $y = 0$, ta được điểm O(0;0).

+ Với $x = 1$ thì $y = 3$, ta được điểm A(1;3).

Đồ thị hàm số $y = 2x + 2$ là đường thẳng đi qua hai điểm O(0;0) và A(1;3)

Ta có đồ thị:

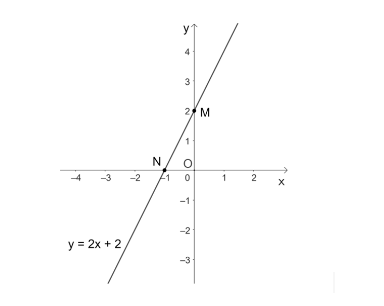
Hàm số: $y = 2x + 2$

+ Với $x = 0$ thì $y = 2$, ta được điểm M(0;2) 

+ Với $y = 0$ thì $x = -1$, ta được điểm N(-1;0) 

=> Đồ thị hàm số $y = 2x + 2$ là đường thẳng đi qua hai điểm M(0;2) và N(-1;0)

Ta có đồ thị:

III. Hệ số góc của đường thẳng y = ax + b (a≠0)

1. Góc tạo bởi đường thẳng y = ax + b (a≠0) và trục Ox

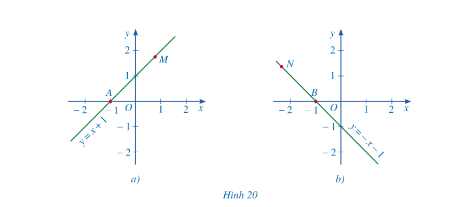
Bài 1: Quan sát các đường thẳng $y = x + 1$ và $y = - x - 1$ (hình 20) 

a. Tung độ các điểm M, N là số dương hay âm ?

b. Tìm góc tạo bởi 2 tia Ax và AM ở hình 20a.

c. Tìm góc tạo bởi 2 tia Bx và BN ở hình 20b.

Đáp án:

a) Hình 20a): Tung độ các điểm M là số dương do điểm M nằm trong góc phần tư thứ I

Hình 20b): Tung độ các điểm N là số âm do điểm N nằm trong góc phần tư thứ II  .

b) $\widehat{MAx}$ là góc tạo bởi hai tia Ax và AM

c) $\widehat{NBx}$ là góc tạo bởi hai tia Bx và BN

2. Hệ số góc

Bài 2: Hình 22 a biểu diễn đồ thị của hàm số bậc nhất $y = 0,5x + 2;  y = 2x + 2$. Hình 22b biểu diễn đồ thị của hàm số bậc nhất $y = 2x + 2; y = -0,5x + 2$.

a) Quan sát Hình 22a, so sánh các góc α, β và so sánh các giá trị tương ứng của hệ số của x trong các hàm số bậc nhất rồi rút ra nhận xét.

b) Quan sát Hình 22b, so sánh các góc α′, β′ và so sánh các giá trị tương ứng của hệ số của x trong các hàm số bậc nhất rồi rút ra nhận xét.

Đáp án: 

- Hình 22a, ta thấy: 

+ Góc α  < Góc β

+ Hàm số $y = 0,5x + 2$ và $y = 2x+2$ có hệ số của x lần lượt là 0,5 và 2.

=> Do 2 > 0,5 nên hệ số $x$ của hàm số $y = 0,5x + 2$ nhỏ hơn hệ số x của hàm số $y = 2x + 2$.

- Hình 22b:

+ Góc α' > Góc β'

+ Hàm số $y = -2x + 2$ và $y = -0,5x + 2$ lần lượt có hệ số của x là -2 và -0,5

=> Do -2 < -0,5 Hệ số x của hàm số $y = -2x + 2$ nhỏ hơn hệ số x của hàm số $y = -0,5x + 2$.

Bài 3: Tìm hệ số góc của đường thẳng $y = - 5x + 11$

Đáp án:

Hệ số góc là -5.

3. Ứng dụng của hệ số góc

Bài 4: 

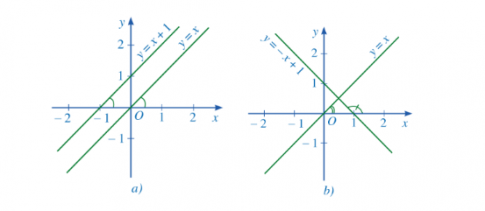
a) Quan sát Hình 23a, tìm hệ số góc của hai đường thẳng $y = x$ và $y = x + 1$ và nêu vị trí tương đối của hai đường thẳng đó.

b) Quan sát Hình 23b, tìm hệ số góc của hai đường thẳng $y = x$ và $y = - x + 1$ và nêu vị trí tương đối của hai đường thẳng đó.

Đáp án:

a) 

Ta có hai góc tạo từ hai đường thẳng tạo với trục Ox bẳng nhau 

=> Hai đường thẳng $y = x$ và $y = x + 1$ song song với nhau (đồng vị)

b) 

Trong Hình 23b) hai đường thẳng $y = x$ và $y = –x + 1$ vuông góc với nhau.

Bài 5: Xét vị trí tương đối của hai đường thẳng $y = -5x$ và $y = -5x + 2$.

Đáp án:

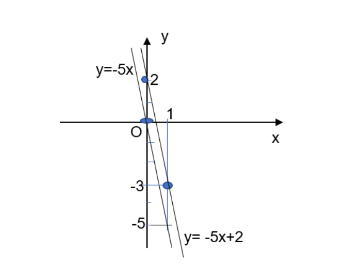
Ta thấy đường thẳng $y = -5x$ và $y = -5x + 2$ có $a = a', b ≠ b'$ ⟺ $-5 = -5; 0 ≠ 2$

=> Hai đường thẳng này song song với nhau.

IV. Bài tập

Bài 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai về đường thẳng d là đồ thị của hàm số y = ax + b (a ≠ 0)?

a) Đường thẳng d cắt trục tung tại điểm có tung độ bằng $-\frac{b}{a}$

b) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng b

c) Đường thẳng d cắt trục tung tại điểm có tung độ bằng b.

d) Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng -ba.

Đáp án:

a) Đúng

b) Đúng

c) Sai do đường thẳng d cắt trục Ox tại điểm có tung độ là $-\frac{b}{a}$

d) Sai do đường thẳng d cắt trục Oy tại điểm có hoành độ bằng b

Bài 2: Chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song trong số các đường thẳng sau: $y = -2x + 5; y = -2x; y = 4x - 1$

Đáp án:

* Các cặp đường thẳng cắt nhau khi có hệ số góc khác nhau. Vậy các đường thẳng cắt nhau là :

$y = -2x + 5$ và $y = 4x - 1 (-2 ≠ 4)$

$y = -2x$ và $y = 4x - 1 (-2 ≠ 4)$

* Các cặp đường thẳng song song với nhau khi có hệ số góc bằng nhau và hệ số tự do khác nhau. Vậy các đường thẳng song song với nhau là:

$y = -2x + 5$ và $y = -2x$ vì có hệ số góc bằng nhau $(-2 = -2)$ và hệ số tự do khác nhau $(5 ≠ 0)$.

Bài 3: $y = 3x; y = 3x + 4; y = -\frac{1}{2}x; y = -\frac{1}{2}x + 3$

Đáp án:

* Đồ thị hàm số: $y = 3x$

+ Với $x = 1$ => $y = 3.1 = 3$, ta được điểm A(1;3)

=> Đồ thị của hàm số $y = 3x$ là đường thẳng đi qua hai điểm O(0;0) và A(1;3)

* Đồ thị hàm số: $y = 3x + 4$

+ Với $x = 0$ => $y = 3.0 + 4 = 4$, ta được điểm B(0;4)

+ Với $y = 0$ => $x = \frac{-4}{3}$, ta được điểm C-43;0

=> đồ thị hàm số $y = 3x + 4$ đi qua điểm B(0;4) và C-43;0

* Đồ thị hàm số: $y=-\frac{1}{2}x$

+ Với $x = 2$ => $y = -\frac{1}{2} . 2 = -1$, Ta được điểm M(2; -1)

=> đồ thị hàm số $y = -\frac{1}{2}x$ là đường thẳng đi qua điểm O(0;0) và điểm M(2; -1)

* Đồ thị hàm số: $y= -\frac{1}{2}x + 3$

+ Với $x = 0$ => $y = 3$, ta được điểm N(0;3)

+ Với $y = 0$ => $x = 6$, ta được điểm P(6;0)

=> Đồ thị hàm số $y = \frac{-1}{2}x + 3$ là đường thẳng đi qua hai điểm N(0;3) và P(6;0)

Vẽ trên cùng một trục tọa độ ta có :

Bài 4: Xác định đường thẳng y = ax + b (a ≠ 0) có hệ số góc bằng - 1 và đi qua điểm M(1; 2). Sau đó vẽ đường thẳng tìm được trên mặt phẳng toạ độ.

Đáp án:

Đường thẳng có dạng $y = -x + b$ (theo đề bài)

Mặt khác, đường thẳng đi qua điểm M(1; 2) nên ta có:

–1 + b = 2 ⬄ b = 3.

Do đó, đường thẳng cần tìm là $y = -x + 3$.

+ Với x=0 => y=3, ta được điểm A(0;3)

+ Với y=0 => x=3, ta được điểm B(3;0)

Do đó, đồ thị của hàm số $y = -x + 3$ là đường thẳng đi qua hai điểm A(0; 3) và B(3; 0).

Ta vẽ đồ thị hàm số như sau:

Bài 5:

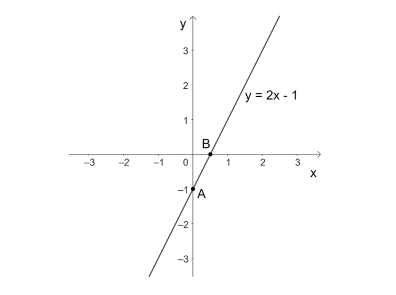
a) Vẽ đường thẳng y = 2x - 1 trong mặt phẳng toạ độ.

b) Xác định đường thẳng y = ax + b (a ≠ 0) đi qua điểm M(1 ; 3) và song song với đường thẳng y = 2x - 1. Sau đó vẽ đường thắng tìm được trên mặt phẳng toạ độ.

Đáp án:

a) Đường thẳng y = 2x - 1 do 

+ Với x = 0 => y = -1, ta được điểm A(0;-1)

+ Với y = 0 => $x = \frac{1}{2}$, ta được điểm $B(\frac{1}{2};0)$

=> Đồ thị của hàm số y = 2x - 1 là đường thẳng đi qua hai điểm $A(0; -1)$ và $B(\frac{1}{2};0)$

Ta vẽ được đồ thị như sau :

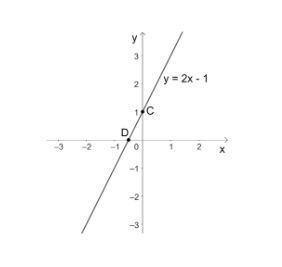
b) Đường thẳng có dạng y = 2x + b do song song với đường thẳng y = 2x - 1

Mặt khác, đường thẳng y = 2x + b đi qua điểm M(1;3) 

=> 2.1 + b = 3 ⬄ b=1.

=> Đường thẳng cần tìm là y = 2x + 1.

+ Với x = 0 => y = 1, ta được điểm A(0;1)

+ Với y = 0 => $x = -\frac{1}{2}$, ta được điểm B($\frac{-1}{2};0$)

=> Đồ thị của hàm số y=2x+1 là đường thẳng đi qua hai điểm $C(0;1)$ và $D(\frac{-1}{2};0)$

Ta vẽ được đồ thị hàm số như sau :

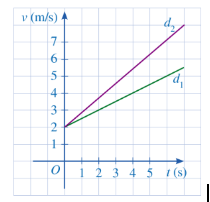
Bài 6: Một phân đường thẳng $d_1; d_2$ ở Hình 24 lần lượt biểu thị tốc độ (đơn vị: m/s) của vật thứ nhất, vật thứ hai theo thời gian t(s).

a) Nêu nhận xét về tung độ giao điểm của hai đường thẳng $d_1; d_2$. Từ đó, nêu nhận xét về tốc độ ban đầu của hai chuyển động.

b) Trong hai đường thẳng d1; d2 đường thẳng nào có hệ số góc lớn hơn?

c) Từ giây thứ nhất trở đi, vật nào có tốc độ lớn hơn? Vì sao?

Đáp án:

a) Hai đường thẳng $d_1, d_2$ đều cắt trục tung tại điểm có tung độ bằng 2.

Do đó, tốc độ ban đầu của hai chuyển động bằng nhau.

b) Trong hình vẽ, ta thấy góc tạo bởi đường thẳng d và đường thẳng $d_2$ lớn hơn góc tạo bởi đường thẳng d và đường thẳng $d_1$.

Mà d//Ox nên suy ra góc tạo bởi đường thẳng Ox và đường thẳng $d_2$ lớn hơn góc tạo bởi đường thẳng Ox và đường thẳng $d_1$.

Do đó, trong hai đường thẳng $d_1, d_2$, đường thẳng $d_2$ có hệ số góc lớn hơn.

c) 

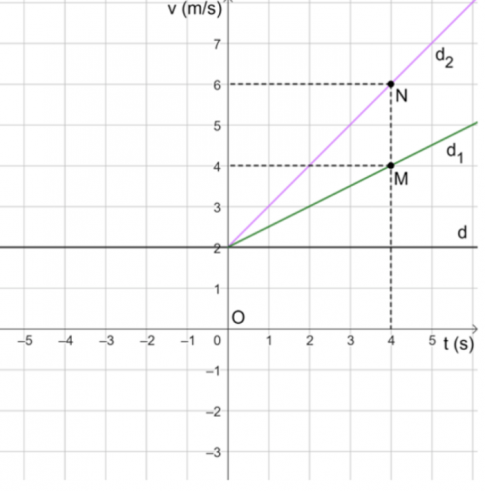
Trên hai đường thẳng $d_1, d_2$ ta lấy hai điểm M, N bất kì có cùng hoành độ (với t >1), ta kẻ hai đường thẳng vuông góc với trục tung.

Do đó, tung độ của điểm N lớn hơn tung độ của điểm M.

Khi đó, vật thứ hai có tốc độ lớn hơn.

Vậy từ giây thứ nhất trở đi, vật thứ hai có tốc độ lớn hơn.