Bài 1: Quan sát các hình 4, 14 và tìm số thích hợp cho ? trong bảng sau: 

Đáp án:

Bài 2: Trong các miếng bìa ở hình 21a, 21b, 21c, 21d, miếng bìa nào có thể gấp (theo các nét đứt) và dán lại để được hình chóp tam giác đều? Hình chóp tứ giác đều?

Đáp án:

Trong các hình trên chỉ có hình 21c thỏa mãn để gấp và dán lại được hình chóp tam giác đều.

Trong các hình trên chỉ có hình 21a thỏa mãn để gấp và dán lại được hình chóp tứ giác đều.

Bài 3: Cho một hình chóp tam giác đều có độ dài cạnh đáy là 20 cm và độ dài trung đoạn là 30 cm. Tính diện tích xung quanh của hình chóp tam giác đều đó.

Đáp án:

$S_{xq}$ của hình chóp tam giác đều đó là:

$S_{xq} = \frac{1}{2}.(20.3).30 = 900 (cm^2)$

Bài 4 : Cho một hình chóp tứ giác đều có độ dài cạnh đáy là 10 cm và độ dài trung đoạn là 13 cm. Tính diện tích xung quanh của hình chóp tứ giác đều đó.

Đáp án:

$S_{xq}$ của hình chóp tứ giác đều đó là:

$S_{xq} = \frac{1}{2}.(10.4).13=260 (cm^2)$

Bài 5: Hình 22 mô tả một vật thể có dạng hình chóp tứ giác đều được tạo ra sau khi cắt bỏ một phần từ một khúc gỗ có dạng hình lập phương với cạnh là 30 cm. Tính thể tích của phần khúc gỗ đã bị cắt bỏ.

Đáp án:

Thể tích của hình lập phương là:

$V_1 = 30^3 = 27 000 (cm^3)$.

Thể tích của vật thể có dạng hình chóp tứ giác đều là:

$V_2 = \frac{1}{3}.30^2.30 = 9000 (cm^3)$

Vậy thể tích của phần đã bị cắt bỏ là:

$V = V_1 – V_2 = 27 000 – 9 000 = 18 000 (cm^3)$.

Bài 6: Hình 23 mô tả một lều trại gồm hai phần: phần dưới có dạng hình lập phương với cạnh là 3 m; phần trên có dạng hình chóp tứ giác đều với chiều cao là 1,8 m. Tính thể tích của lều trại đó.

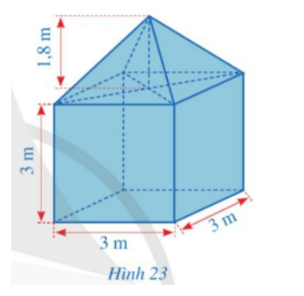
Đáp án:

Thể tích của phần dưới là: $V_1 = 3^3 = 27 (m^3)$

Thể tích của phần trên là: $V_2 = \frac{1}{3}.3^2.1,8 = 5,4 (m^3)$ 

Thể tích của lều trại đó là: $V = V_1 + V_2 = 27 + 5,4 = 32,4 (m^3)$