I. Định nghĩa

Bài 1: Chu vi y (cm) của hình vuông có độ dài cạnh x (cm) được tính theo công thức y = 4x. Với mỗi giá trị của x, xác định được bao nhiêu giá trị tương ứng của y?

Đáp án:

Chu vi y (cm) và độ dài cạnh x (cm) đều là các giá trị dương. Vì thế, với mỗi giá trị của x, ta chỉ nhận được một giá trị tương ứng của y.

Ví dụ: $x = 3 => y = 4 . 3 = 12 (cm)$

$x = \frac{1}{2} => y=4.\frac{1}{2}=2 (cm)$

Bài 2: Trong tình huống ở phần mở đầu, hãy cho biết:

a) Số tiền người bán thu được khi lần lượt bán 2 kg thanh long; 3 kg thanh long.

b) Gọi y (đồng) là số tiền người bán thu được khi bán x (kg) thanh long. Với mỗi giá trị của x, ta xác định được bao nhiêu giá trị tương ứng của y?

Đáp án:

a) Khi bán 2kg thanh long người bán nhận được số tiền là:

$2 . 32 000=64 000$ (đồng)

Khi bán 3kg thanh long người bán nhận được số tiền là:

$3 . 32 000=96 000$ (đồng)

b) Với mỗi giá trị của x ta chỉ có thể nhận được duy nhất một giá trị tương ứng của y.

Bài 3: Cho hai ví dụ về hàm số.

Đáp án:

$y=\frac{3}{5}x; y=10x$ 

II. Giá trị của hàm số.

Bài 1: Một xe ô tô chạy với tốc độ $60 km/h$ trong thời gian t(h).

a) Viết hàm số biểu thị quãng đường $S(t) (km)$ mà ô tô đi được trong thời gian t(h).

b) Tính quãng đường $S(t) (km)$ mà ô tô đi được trong thời gian $t = 2 (h); t = 3 (h)$.

Đáp án:

a) Vận tốc của ô tô là $60 km/h$.

Ta có, hàm số biểu thị độ dài quãng đường $S(t) (km)$ mà ô tô đi trong thời gian t(h) là: $S(t)=60.t (km)$.

b) Với $t=2 (h)$, ô tô đi được quãng đường là: 

$S(2)=60 . 2=120 (km)$;

Với $t=3 h$, ô tô đi được quãng đường là:

$S(3)=60 . 3=180 (km)$.

Bài 2: Cho hàm số: $f(x) = -5x + 3$. Tính $f(0); f(-1); f(\frac{1}{2})$

Đáp án:

III) Bài tập

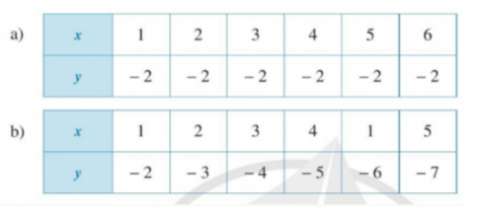
Bài 1: Đại lượng y có phải là hàm số của đại lượng x hay không nếu bảng giá trị tương ứng của chúng được cho bởi mỗi trường hợp sau:

Đáp án:

a) Quan sát bảng trên ta thấy với $x = 1, 2, 3, 4, 5, 6$ thì nhận được giá trị y là $y = - 2$.

Vì mỗi giá trị của x ta chỉ xác định được một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.

b) Quan sát bảng trên ta thấy khi $x=1; x=2; x=3; x=4; x=1; x=5$ thì ta đều xác định  giá trị của y lần lượt là: $y=- 2; y=- 3; y=- 4; y=- 5; y=- 6; y=- 7$.

Vì mỗi giá trị của x ta chỉ xác định được một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.

Bài 2: 

Cho hàm số $y = 2x + 10$. Tìm giá trị của y tương ứng với mỗi giá trị sau của $x: x = -5; x = 0; x = \frac{1}{2}$

Cho hàm số $f(x) = −2x^2+1$. Tính $f(-1);  f(0);  f(1); f(\frac{1}{3})$

Đáp án:

a) 

b) 

Bài 3: Cho một thanh kim loại đồng chất có khối lượng riêng là $7,8 g/cm^3$.

a) Viết công thức tính khối lượng m (g) theo thể tích $V (cm^3)$. Hỏi m có phải là hàm số của V hay không? Vì sao?

b) Tính khối lượng của thanh kim loại đó khi biết thể tích của thanh kim loại đó là $V = 1 000 cm^3$.

Đáp án:

a) Công thức tính khối lượng $m (g)$ theo thể tích $V (cm^3)$ là: $m=\frac{V}{7,8}$

Với mỗi giá trị của V ta nhận được một giá trị của m nên m là hàm số của V.

b) Thay $V=1 000 cm^3$, khối lượng của thanh kim loại đó là:

$m=\frac{1000}{7,8}=\frac{5000}{39} (g)$

Bài 4: Dừa sáp là một trong những đặc sản lạ, quý hiếm và có giá trị dinh dưỡng cao, thường được trồng ở Bến Tre hoặc Trà Vinh. Giá bán mỗi quả dừa sáp là 200 000 đồng.

a) Viết công thức biểu thị số tiền y (đồng) mà người mua phải trả khi mua x (quả) dừa sáp. Hỏi y có phải là hàm số của x hay không? Vì sao?

b) Hãy tính số tiền mà người mua phải trả khi mua 10 quả dừa sáp.

Đáp án:

a) Công thức biểu thị số tiền y (đồng) phải trả khi mua x (quả) dừa sáp là : $y=200 000x$ (đồng) .

Với mỗi giá trị x ta xác định được một giá trị y tương ứng nên y là hàm số của x.

b) Khi mua 10 quả dừa sáp, người mua phải trả số tiền là:

$200 000 . 10=2 000 000$ (đồng).

Bài 5: Bác Ninh gửi tiết kiệm 10 triệu đồng ở ngân hàng với kì hạn 12 tháng và không rút tiền trước kì hạn. Lãi suất ngân hàng quy định cho kì hạn 12 tháng là r%/năm.

a) Viết công thức biểu thị số tiền lãi y (đồng) theo lãi suất r%/năm mà bác Ninh nhận được khi hết kì hạn 12 tháng. Hỏi y có phải là hàm số của r hay không? Vì sao?

b) Tính số tiền lãi mà bác Ninh nhận được khi hết kì hạn 12 tháng, biết r = 5,6.

Đáp án:

a) Công thức biểu thị số tiền lãi y (đồng) theo lãi suất r%/năm mà bác Ninh nhận được khi hết kì hạn 12 tháng là: y=10r% (triệu đồng).

Với mỗi giá trị r thì ta xác định được một giá trị tương ứng y nên y là hàm số của r.

b) Với $r=5,6$ sau khi hết kì hạn 12 tháng, Bác Ninh sẽ nhận được số tiền là:

$y=10r%=10 . 5,6%=0,56$ (triệu đồng) $=560 000$ (đồng).