I. Định nghĩa

Bài 1: Cho biết số đo mỗi góc của tứ giác ABCD trong hình 47.  

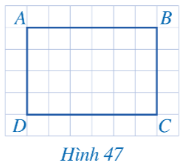
Đáp án:

Trong Hình 47, tứ giác ABCD có các góc: $\widehat{A}, \widehat{B}, \widehat{C}, \widehat{D}$ đều bằng nhau và bằng $90^{\circ}$

II. Tính chất

Bài 1: 

a) Mỗi hình chữ nhật có là một hình thang cân hay không?

b) Mỗi hình chữ nhật có là một hình bình hành hay không?

Đáp án:

a) Là một hình thang cân (do nó là hình thang có hai góc kề một đáy bằng nhau).

b) Là một hình bình hành (do nó có hai cặp góc đối bằng nhau).

Bài 2: Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N lần lược là hình chiếu của O trên AB, BC. Chứng minh $MN = \frac{1}{2}AC$.

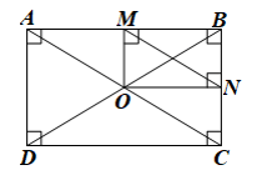
Đáp án:

Gọi M, N là hình chiếu của O lên AB, AC

$=> OM⊥AB$ và $ON⊥BC$

Xét tứ giác OMBN:

$\widehat{OMB}=\widehat{MBN}=\widehat{BNO}=90^{\circ}$

Do đó tứ giác OMBN là hình chữ nhật $=> OB=MN$

Do ABCD là hình chữ nhật => $OB=OD=MN=\frac{1}{2}AC$

=> $MN=OB=\frac{1}{2}AC$

III. Dấu hiệu nhận biết

Bài 1: 

a) Cho hình bình hành $ABCD$ có $\widehat{A}=90^{\circ}. ABCD$ có phải là hình chữ nhật hay không?

b) Cho hình bình hành ABCD có hai đường chéo AC và BD bằng nhau (Hình 50):

Hai tam giác ABC và DCB có bằng nhau hay không? Từ đó, hãy so sánh $\widehat{ABC}$ và $\widehat{DCB}$.

ABCD có phải là hình chữ nhật hay không?

Đáp án:

a) Xét hình bình hành $ABCD$

=> $AB//CD$ và $\widehat{C}=\widehat{A}=90^{\circ}; \widehat{B}=\widehat{D}$

Do $AB//CD => \widehat{A}+\widehat{D}=180^{\circ}$

=> $\widehat{D}=180^{\circ}-90^{\circ}=90^{\circ}$

=> $\widehat{A}=\widehat{C}=\widehat{B}=\widehat{D}=90^{\circ}$ nên $ABCD$ là hình chữ nhật.

b)

Xét ∆ABC và ∆DCB có:

$BC$ chung

$AB=DC$ ($ABCD$ là hình bình hành)

 $AC=DB (gt)$

=> $∆ABC=∆DCB (c.c.c)$

=> $\widehat{ABC}=\widehat{DCB}$

Do $AB//CD$ ($ABCD$ là hình bình hành) 

=> $\widehat{ABC}+\widehat{DCB}=180^{\circ}$

=> $2\widehat{ABC}=180^{\circ} => \widehat{ABC}=90^{\circ}$

Vậy hình bình hành ABCD có 1 góc vuông nên là hình chữ nhật.

Bài 2: Cho hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O thoả mãn $\widehat{OAB}=\widehat{ODC}$. Chứng minh $ABCD$ là hình chữ nhật.

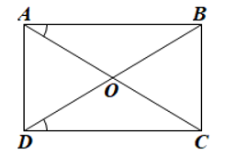
Đáp án:

Ta có $AB//CD$ ($ABCD$ là HBH) 

=> $\widehat{CAB}=\widehat{ACD}$ hay $\widehat{OAB}=\widehat{OCD}$ (so le trong)

Mà $\widehat{OAB}=\widehat{ODC}$ (gt) => $\widehat{ODC}=\widehat{OCD}$

Xét ∆ODC: $\widehat{ODC}=\widehat{OCD}$ (cmt)

=> $∆ODC$ cân tại O => $OD=OC$. Mà $OA=OC; OB=OD$

=> $OA=OB=OC=OD$ => $AC=BD$

Hình bình hành ABCD có hai đường chéo AC=BD nên là hình chữ nhật.

IV. Bài tập

Bài 1: Cho hình thang cân ABCD có $AB // CD, \widehat{A}=90^{\circ}$. Chứng minh ABCD là hình chữ nhật.

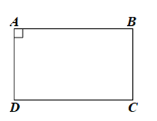
Đáp án:

Xét hình thang cân $ABCD$ có $AB//CD$

=> $\widehat{B}=\widehat{A}=90^{\circ}; \widehat{C}=\widehat{D}$

Vì $AB//CD$ => $\widehat{A}+\widehat{D}=180^{\circ}$

=>$\widehat{D}=180^{\circ}-\widehat{A}=90^{\circ}$

Do đó hình thang cân ABCD có $\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^{\circ}$ nên là hình chữ nhật. 

Bài 2: Cho tam giác ABC vuông tại A có M là trung điểm cúa cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho $MD = MA$. Chứng minh tứ giác $ABDC$ là hình chữ nhật và $AM = \frac{1}{2}BC$

Đáp án:

Ta có: M là trung điểm của $AD (MD=MA)$

Xét tứ giác $ABCD$ có 

AD và BC là hai đường chéo cắt nhau tại trung điểm M của mỗi đường

=> ABCD là hình bình hành. Mà $\widehat{BAC}=90^{\circ}$

=> Hình bình hành $ABCD$ là hình chữ nhật.

=> $AD=BC$, mà $AM=\frac{1}{2}AD => AM=\frac{1}{2}BC$.

Bài 3: Cho hình chữ nhật ABCD có điểm E nằm trên cạnh CD sao cho $\widehat{AEB} = 78^{\circ}, \widehat{EBC} = 39^{\circ}$. Tính số đo của $\widehat{BEC}$ và $\widehat{EAB}$.

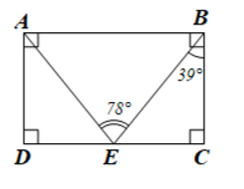
Đáp án:

∆BEC vuông tại C có:

$\widehat{BEC}+\widehat{EBC}=90^{\circ}$ 

$\Rightarrow \widehat{BEC}=90^{\circ}-39^{\circ}=51^{\circ}$

Ta có: $\widehat{ABE}+\widehat{CBE}=90^{\circ} => \widehat{CBE} = 51^{\circ}$

Xét ∆ABE có : $\widehat{EAB}+\widehat{ABE}+\widehat{AEB}=180^{\circ}$ 

=> $\widehat{EAB}=180^{\circ}-\widehat{ABE}-\widehat{AEB}=180^{\circ}-51^{\circ}-78^{\circ}=51^{\circ}$

Bài 4: Một khu vườn có dạng tứ giác ABCD với các góc A, B, D là góc vuông, $AB = 400 m, AD = 300 m$. Người ta đã làm một cái hồ nước có dạng hình tròn, khi đó vị trí C không còn nằm trong khu vườn nữa (Hình 52). Tính khoảng cách từ vị trí C đến mỗi vị trí A, B, D.

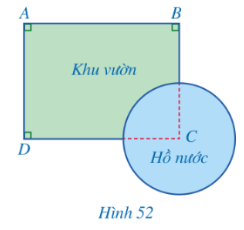
Đáp án:

Xét tứ giác $ABCD$ có $\widehat{A}=\widehat{B}=\widehat{D}=90^{\circ}$ 

=> $ABCD$ là hình chữ nhật.

=> $CB=AD=300 m;CD=AB=400 m$

Xét ∆ABC vuông tại B, 

$AC^2=AB^2+BC^2$ (định lí Pythagore)

=> $AC=\sqrt{AB^2+BC^2}=\sqrt{400^2+300^2}=500 (m)$

Vậy khoảng cách từ vị trí C đến mỗi vị trí $A, B, D$ lần lượt là $500 m, 300 m$ và $400 m$.

Bài 5: Bạn Linh có một mảnh giấy dạng hình tròn. Bạn Linh đố bạn Bình: Làm thế nào có thể chọn ra 4 vị trí trên đường tròn đó để chúng là 4 đỉnh của một hình chữ nhật? Bạn Bình đã làm như sau:

Bước 1: Gấp mảnh giấy sao cho hai nửa hình tròn trùng khít nhau. Nét gấp thẳng tạo thành đường kính của hình tròn. Ta đánh dấu hai đầu mút của đường kính đó là hai điểm A, C.

Bước 2. Sau đó lại gấp tương tự mảnh giấy đó nhưng theo đường kính mới và đánh dấu hai đầu mút của đường kính mới là hai điểm B, D. Khi đó tứ giác ABCD là hình chữ nhật (Hình 53).

Em hãy giải thích cách làm của bạn Bình.

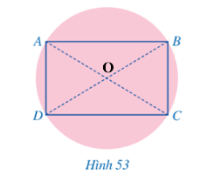
Đáp án:

Gọi $AC∩BD=O$ 

=> $OA=OB=OC=OD$ (cùng bằng bán kính)

Tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm O của mỗi đường nên là hình bình hành.

Mặt khác AC và BD là đường kính của hình tròn => $AC=BD$

Xét hình bình hành ABCD có hai đường chéo $AC=BD$ 

$\Rightarrow ABCD$ là hình chữ nhật.