HẰNG ĐẲNG THỨC

Bài 1: Xét hai biểu thức: P = 2(x + y) và Q = 2x + 2y. Tính giá trị của mỗi biểu thức P và Q rồi so sánh hai giá trị đó trong mỗi trường hợp sau:

Tại x = 1; y = - 1.

Tại x = 2; y = - 3

Đáp án:

a) Tại x = 1; y = −1, ta có:

P = 2 . [1 + (−1)] = 2 . 0 = 0;

Q = 2 . 1 + 2 . (−1) = 2 – 2 = 0.

Vậy tại x = 1; y = −1 thì P = Q.

b) Tại x = 2; y = −3, ta có:

P = 2 . [2 + (−3)] = 2 . (−1) = −2;

Q = 2 . 2 + 2 . (−3) = 4 – 6 = −2.

Vậy tại x = 2; y = −3 thì P = Q. 

Bài 2: Chứng minh rằng:…

Đáp án:

$x(xy^2 + y) – y(x^2y + x) = x . xy^2 + x . y – y . x^2y – y . x$

= $x^2y^2 + xy – x^2y^2 – xy = 0$ (đpcm)

HẰNG ĐẲNG THỨC ĐÁNG NHỚ

1. Bình phương của một tổng, hiệu

Bài 1: Với a, b là 2 số thức bất kì, thực hiện phép tính: 

a) (a + b)(a + b) 

b) (a - b)(a - b)

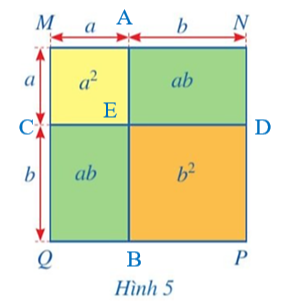
Đáp án:

a) $(a + b)(a + b) = a . a + a . b + b . a + b . b = a^2 + 2ab + b^2$;

Vậy với 2 số thức bất kì $(a + b)(a + b) = a^2 + 2ab + b^2$

$(a – b)(a – b) = a . a – a . b – b . a + b . b = a^2 – 2ab + b^2$.

Vậy với 2 số thức bất kì $(a - b)(a - b) = a^2 - 2ab + b^2$

Bài 3: Tính:…

Đáp án:

a) $(x + \frac{1}{2})^2 = x^2 + 2 . x . \frac{1}{2} + (\frac{1}{2})^2$

= $x^2 + x + \frac{1}{4}$ 

b) $(2x + y)^2 = (2x)^2 + 2 . 2x . y + y^2$ 

= $4x^2 + 4xy + y^2$

c) $(3 – x)^2 = 3^2 – 2 . 3 . x + x^2 = 9 – 6x + x^2$

d) $(x – 4y)^2 = x^2 – 2 . x . 4y + (4y)^2$ 

= $x^2 – 8xy + 16y^2$.

Bài 4: Viết mỗi biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

Đáp án:

a) $y^2+ y + 14 = y^2 + 2.12.y + (\frac{1}{2})^2$

= $(y + \frac{1}{2})^2$

b) $y^2+ 49 – 14y = y^2 – 2 . 7 . y + 7^2 = (y – 7)^2$.

Bài 5: Tính nhanh $49^2$

Đáp án:

$49^2$ = $(50 - 1)^2$ = $50^2 - 2 . 50 . 1 + 1^2$ = $2500 - 100 + 1$ = $2401$.

2. Hiệu của hai bình phương

Bài 6: Với a, b là 2 số thực bất kì. Thực hiện phép tính: (a - b)(a + b)

Đáp án:

$(a – b)(a + b) = a . a + a . b – b . a + b . b = a^2 – b^2$.

Vậy với a, b là 2 số thực bất kì: $(a – b)(a + b) = a^2 – b2$

Bài 7: Viết biểu thức sau dưới dạng tích:…

Đáp án:

a) $9x^2– 16 = (3x)^2– 4^2 = (3x + 4)(3x – 4)$

b) $25 – 16y^2 = 5^2– (4y)^2 = (5 + 4y)(5 – 4y)$.

Bài 8: Tính:…

Đáp án:

a) $(a – 3b)(a + 3b) = a^2 – (3b)^2 = a^2 – 9b^2$

b) $(2x + 5)(2x – 5) = (2x)^2 – 5^2 = 4x^2 – 25$

c) $(4y – 1)(4y + 1) = (4y)^2 – 1 = 16y^2 – 1$.

Bài 9: Tính nhanh 48.52

Đáp án:

$48 . 52 = (50 – 2)(50 + 2) = 50^2 – 2^2$ 

= $2500 – 4 = 2496$.

3. Lập phương của một tổng, một hiệu

Bài 10: Với a, b là 2 số thực bất kì, thực hiện phép tính:…

Đáp án:

a) $(a + b)(a + b)^2 = (a + b)(a^2 + 2ab + b^2)$

= $a(a^2 + 2ab + b^2) + b(a^2 + 2ab + b^2)$

= $a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3$

= $a^3 + 3a^2b + 3ab^2 + b^3$.

b) $(a – b)(a^2 – 2ab + b^2)$

= $a(a^2 – 2ab + b^2) – b(a^2 – 2ab + b^2)$

= $a^3 – 2a^2b + ab^2 – a^2b + 2ab^2 – b^3$

= $a^3 – 3a^2b + 3ab^2 – b^3$.

Bài 11: Tính:…

Đáp án:

a) $(3 + x)^2 = 3^3 + 3 . 3^2 . x + 3 . 3 . x^2 + x^3$ 

= $27 + 27x + 9x^2 + x^3$

b) $(a + 2b)^3 = a^3 + 3 . a^2 . 2b + 3 . a . (2b)^2 + (2b)^3$

= $a^3 + 6a^2b + 12ab^2 + 8b^3$

c) $(2x – y)^3 = 2x^3 - 3 . (2x)^2 . y + 3 . 2x . y^2 - y^3$ 

= $8x^3 - 12x^2y + 6xy^2 - y^3$ 

Bài 12: Viết biểu thức sau dưới dạng lập phương của một hiệu:…

Đáp án:

$8x^3 – 36x^2y + 54xy^2 – 27y^3$

= $(2x)^3 – 3 . (2x)^2 . 3y + 3 . 2x . (3y)^2 – (3y)^3$

= $(2x – 3y)^3$.

Bài 13: Tính nhanh...

Đáp án:

$101^3 – 3 . 101^2 + 3 . 101 – 1= 101^3 – 3 . 101^2 . 1 + 3 . 101 . 1^2 – 1^3$

= $(101 – 1)^3 = 100^3 = 1 000 000$.

4. Tổng và hiệu của hai lập phương

Bài 14:  Với a, b là hai số thực bất kì, thực hiện phép tính: …

Đáp án:

a) $(a + b)(a^2– ab + b^2)$ 

= $a . a^2 – a . ab + a . b^2 + b . a^2 – b . ab + b . b^2$

= $a^3 – a^2b + ab^2 + a^2b – ab^2 + b^3 = a^3 + b^3$.

b) $(a – b)(a^2+ ab + b^2)$ 

= $a . a^2 + a . ab + a . b^2 – b . a^2 – b . ab – b . b^2$

= $a^3 + a^2b + a^2b – a^2b – a^2b – b^3$ 

= $a^3 – b^3$.

Bài 15: Viết mỗi biểu thức sau dưới dạng tích:…

Đáp án:

a) $27x^3 + 1 = (3x)^3 + 13$

= $(3x + 1)[(3x)^2 – 3x . 1 + 1^2]$

b) $64 – 8y^3 = 4^3 – (2y)^3$ 

= $(4 + 2y)(4 – 2y)$.

BÀI TẬP

Bài 1: Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:…

Đáp án:

a) $4x^2 + 28x + 49 = (2x)^2 + 2 . 2x . 7 + 7^2$ 

= $(2x + 7)^2$

b) $4a^2 + 20ab + 25b^2 = (2a)^2 + 2.2a.5b + (5b)^2$ 

= $(2a+5b)^2$

c) $16y^2 – 8y + 1 = (4y)^2 – 2 . 4y . 1 + 1^2$ 

= $(4y – 1)^2$

d) $9x^2 − 6xy + y^2 = (3x)^2 − 2.3x.y + y^2$ 

= $(3x−y)^2$

Bài 2: Viết các biểu thức sau đây dưới dạng lập phương của một tổng hoặc một hiệu…

Đáp án:

a) $a^3 +12a^2 + 48a + 64 = (a + 4)^3$

b) $27x^3 + 54x^2y + 36xy^2 + 8y^3 = (3x+2y)^3$

c) $x^3 – 9x^2 + 27x – 27 = (x – 3)^3$

d) $8a^3 − 12a^2b + 6ab^2 − b^3 = (2a − b)^3$

Bài 3: Viết mỗi biểu thức sau dưới dạng tích:… 

Đáp án:

a) $25x^2 – 16 = (5x)^2 – 4^2 = (5x + 4)(5x – 4)$

b) $8x^3 + 1 = (2x)^3 + 1 = (2x + 1)(4x^2 – 2x + 1)$

c) $8x^3 – 125 = (2x)^3 – 5^3 = (2x – 5)(4x^2 + 10x + 25)$

d) $27x^3 – y^3 = (3x)^3 – y^3 = (3x – y)(9x^2 + 3xy + y^2)$

e) $16a^2 – 9b^2 = (4a)^2 – (3b)^2 = (4a + 3b)(4a – 3b)$

g) $125x^3 + 27y^3 = (5x)^3 + (3y)^3$ 

= $(5x + 3y)(25x^2 – 15xy + 9y^2)$

Bài 4: Tính giá trị của mỗi biểu thức: 

Đáp án:

a) $A = x^2 + 6x + 10 = x^2 + 6x + 9 + 1 = (x + 3)^2 + 1$.

Thay $x = -103$ vào biểu thức A: 

$A = (−103 + 3)^2 + 1 = (−100)^2 + 1 = 10 000 + 1 = 10 001$.

Vậy $A = 10 001$ tại $x = −103$.

b) $B = x^3 + 6x^2 + 12x + 12 = x^3 + 3 . x^2 . 2 + 3 . x . 2^2 + 2^3 + 4$

= $(x + 2)^3 + 4$.

Thay $x = 8$ vào biểu thức B, ta được:

$B = (8 + 2)^3 + 4 = 10^3 + 4 = 1004$.

Vậy $B = 1004$ tại $x = 8$.

Bài 5: Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến x…

Đáp án:

a) $C = (3x – 1)^2 + (3x + 1)^2 – 2(3x – 1)(3x + 1)$

= $[(3x – 1) – (3x + 1)]^2 = (3x – 1 – 3x – 1)^2$

= $(– 1 – 1)^2 = (–2)^2 = 4$.

Vậy C không phụ thuộc vào biến x.

b) $D = (x + 2)^3 – (x – 2)^3 – 12(x^2 + 1)$

= $[(x + 2) – (x – 2)][(x + 2)^2 + (x + 2)(x – 2) + (x – 2)^2] – 12(x^2 + 1)$

= $(x + 2 – x + 2)[(x + 2)^2 + x^2 – 2^2 + (x – 2)^2] – 12x^2 – 12$

= $4(x^2 + 4x + 4 + x^2 – 4 +x^2 – 4x + 4) – 12x^2 – 12$

= $4(3x^2 + 4) – 12x^2 – 12 = 12x^2 + 16 – 12x^2 – 12 = 4$.

Vậy D không phụ thuộc vào biến x.

c) $E = (x + 3)(x^2 – 3x + 9) – (x – 2)(x^2 + 2x + 4)$

= $(x^3 + 3^3) – (x^3 – 2^3)$ 

= $x^3 + 27 – x^3 + 8 = 35$.

Vậy E không phụ thuộc vào biến x.

d) $G = (2x – 1)(4x^2 + 2x + 1) – 8(x + 2)(x^2 – 2x + 4)$

= $[(2x)^3 – 1^3] – 8(x^3 + 2^3) = (8x^3 – 1) – 8(x^3 + 8)$

= $8x^3 – 1 – 8x^3 – 64 = – 65$.

Vậy G không phụ thuộc vào biến x.

Bài 6: Tính nhanh:

Đáp án:

$(0,76)^3 + (0,24)^3 + 3 . 0,76 . 0,24$

= $(0,76 + 0,24)^3 – 3 . 0,76 . 0,24 . (0,76 + 0,24) + 3 . 0,76 . 0,24$

= $1^3 – 3 . 0,76 . 0,24 . 1 + 3 . 0,76 . 0,24$