Giải câu 2 bài Ôn tập cuối năm Phần Đại số sgk Toán 8 tập 2 trang 130
Câu 2: trang 130 sgk Toán 8 tập 2
a)Thực hiện phép chia:
\((2x^4 – 4x^3 + 5x^2 + 2x – 3) \div (2x^2– 1)\)
b) Chứng tỏ rằng thương tìm được trong phép chia trên luôn luôn dương với mọi giá trị của x.
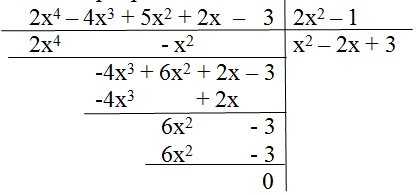
Vậy \((2x^4 – 4x^3 + 5x^2 + 2x – 3) \div (2x^2– 1)=x^2-2x+3\)
b) Ta có:
\({x^2} - 2x + 3 \)
\(= ({x^2} - 2x + 1) + 2\)
\(={\left( {x - 1} \right)^2} + 2 > 0\) với mọi x (đpcm)
Vậy thương tìm được luôn luôn dương với mọi giá trị của x.
Từ khóa tìm kiếm Google: giải câu 2 trang 130 sgk Toán 8 tập 2, giải bài tập 2 trang 130 Toán 8 tập 2, câu 2 trang 130 toán 8 tập 2, Câu 2 bài ôn tập cuối năm - phần đại số - sgk Toán 8 tập 2

Bình luận