Giải toán 8 chân trời bài Bài tập cuối chương 8
Giải bài: Bài tập cuối chương 8 sách toán 8 tập 2 chân trời sáng tạo. Phần đáp án chuẩn, hướng dẫn giải chi tiết cho từng bài tập có trong chương trình học của sách giáo khoa. Hi vọng, các em học sinh hiểu và nắm vững kiến thức bài
Nội dung quan tâm khác
Thêm kiến thức môn học
Từ khóa tìm kiếm: Giải toán 8 chân trời bài Bài tập cuối chương 8, Giải toán 8 tập 2 chân trời sáng tạo bài Bài tập cuối chương 8, Giải toán 8 CTST tập 2 bài Bài tập cuối chương 8

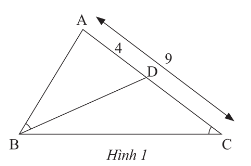
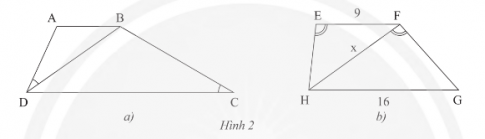
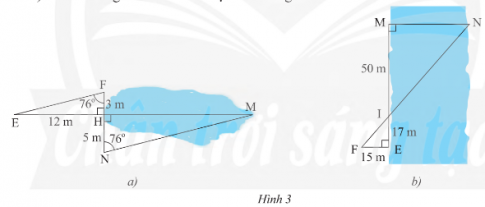
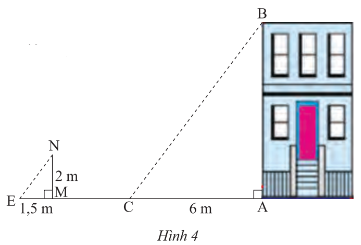

Bình luận