Giải Bài tập 16 trang 86 sgk Toán 8 tập 2 Chân trời

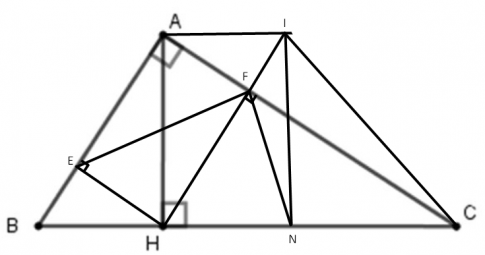
a) Xét tam giác vuông ABH và CBA ta có:

$\widehat{B}$ chung

Suy ra ΔABH ᔕ ΔCBA nên $\frac{AB}{BC}=\frac{BH}{AB}$ hay $AB^{2}=BH.BC$

b) c) Tứ giác AEHF có 4 góc vuông suy ra AEHF là hình chữ nhật 

Do đó $\widehat{AEF}=\widehat{AEH}$

ΔABH ᔕ ΔCBA nên $\widehat{EAH}=\widehat{ACB}$

Xét tam giác AEF và ACB ta có:

$\widehat{A}$ chung

$\widehat{EAH}=\widehat{ACB}$

Suy ra ΔAEF ᔕ ΔACB (g.g) nên $\frac{AE}{AC}=\frac{AF}{AB}$ hay AE. AB = AF . AC

d) Xét tam giác vuông HNI và HFC ta có:

$\widehat{H}$ chung

Suy ra ΔHNI ᔕ ΔHFC (g.g) nên $\frac{HN}{HF}=\frac{HI}{HC}$ hay $\frac{HN}{HI}=\frac{HF}{HC}$

Xét tam giác HNF và HIC ta có:

$\widehat{H}$ chung

$\frac{HN}{HI}=\frac{HF}{HC}$

Suy ra ΔHNF ᔕ ΔHIC (c.g.c)