Giải Bài tập 14 trang 86 sgk Toán 8 tập 2 Chân trời

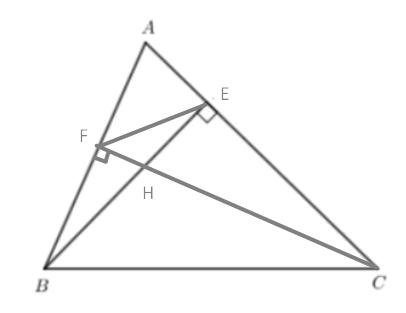
a) Xét tam giác vuông AEB và AFC có:

$\widehat{A}$ chung

Suy ra ΔAEB ᔕ ΔAFC (g.g)

b) Xét tam giác vuông HCE và HBF ta có:

$\widehat{EHC}=\widehat{FHB}$ (hai góc đối đỉnh)

Suy ra ΔHCE ᔕ ΔHBF (g.g) nên $\frac{HE}{HF}=\frac{HC}{HB}$ hay $\frac{HE}{HC}=\frac{HF}{HB}$

c) Xét tam giác HEF và HCB ta có:

$\frac{HE}{HC}=\frac{HF}{HB}$

$\widehat{EHF}=\widehat{BHC}$ (hai góc đối đỉnh)

Suy ra ΔHEF ᔕ ΔHCB (c.g.c)