Giải Bài tập 15 trang 86 sgk Toán 8 tập 2 Chân trời
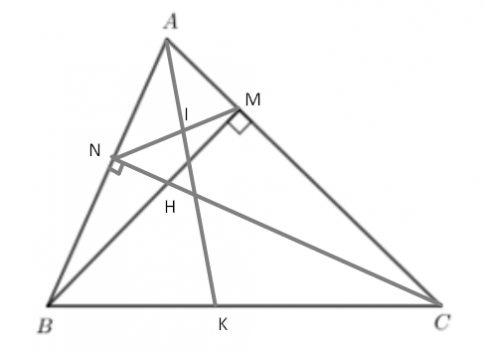
Bài tập 15 trang 86 sgk Toán 8 tập 2 CTST: Cho tam giác ABC nhọn có hai đường cao BM, CN cắt nhau tại H
a) Chứng minh rằng ΔAMN ᔕ ΔABC
b) Phân giác của $\widehat{BAC}$ cắt MN và BC lần lượt tại I và K. Chứng minh rằng $\frac{IM}{IN}=\frac{KB}{KC}$
a) Xét tam giác vuông ABM và ACN có:
$\widehat{A}$ chung
Suy ra ΔABM ᔕ ΔACN (g.g) nên $\frac{AM}{AN}=\frac{AB}{AC}$ hay $\frac{AM}{AB}=\frac{AN}{AC}$
Xét tam giác AMN và ABC ta có:
$\frac{AM}{AB}=\frac{AN}{AC}$
$\widehat{A}$ chung
Suy ra ΔAMN ᔕ ΔABC (c.g.c)
b) ΔAMN ᔕ ΔABC, AK là phân giác của $\widehat{BAC}$ suy ra $\frac{AM}{AB}=\frac{AN}{AC}=\frac{AI}{AK}$
Xét tam giác AIM và AKB ta có:
$\frac{AM}{AB}=\frac{AI}{AK}$
$\widehat{IAM}=\widehat{IAN}$ (vì AK là phân giác $\widehat{BAC}$)
Suy ra ΔAIM ᔕ ΔAKB nên $\frac{IM}{KB}=\frac{AI}{AK}$ (1)
Xét tam giác AIN và AKC ta có:
$\frac{AN}{AC}=\frac{AI}{AK}$
$\widehat{IAM}=\widehat{IAN}$ (vì AK là phân giác $\widehat{BAC}$)
Suy ra ΔAIN ᔕ ΔAKC nên $\frac{IN}{KC}=\frac{AI}{AK}$ (2)
Từ (1) và (2) suy ra $\frac{IM}{KB}=\frac{IN}{KC}$ hay $\frac{IM}{IN}=\frac{KB}{KC}$
Xem toàn bộ: Giải toán 8 chân trời bài Bài tập cuối chương 8

Bình luận