Giải Bài tập 10 trang 85 sgk Toán 8 tập 2 Chân trời

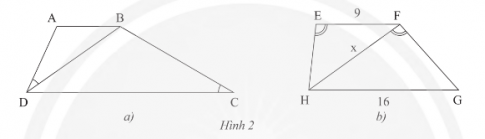
a) Xét tam giác BDC ta có: $\widehat{DBC}+\widehat{BDC}+\widehat{DCB}=180°$

AB // CD => $\widehat{BAD}+\widehat{ADC}=180°$ (hai hóc trong cùng phía) => $\widehat{BAD}+\widehat{ADB}+\widehat{BDC}=180°$

Lại có $\widehat{ADB}=\widehat{DCB}$ nên $\widehat{BAD}=\widehat{DBC}$

Xét tam giác ABD và BDC ta có:

$\widehat{BAD}=\widehat{DBC}$

$\widehat{ADB}=\widehat{DCB}$

Suy ra ΔABD ᔕ ΔBDC (g.g) nên $\frac{AB}{BD}=\frac{BD}{CD}$ hay $BD^{2}=AB.CD$

b) Tương tự câu a, ta có: $\widehat{EHG}=\widehat{FGH}$

Xét tam giác EFH và FHG ta có:

$\widehat{EHG}=\widehat{FGH}$

$\widehat{HEF}=\widehat{HFG}$

Suy ra ΔEFH ᔕ ΔFHG (g.g) nên $\frac{EF}{HF}=\frac{HF}{GH}$ hay $HF^{2}=EF.GH=9 . 16=144$ => HF = 12 (cm)